地图
代价地图的参数定义在三个文件里,分别用于全局代价地图,局部代价地图,通用代价地图(用于两个代价地图的参数)
movebase建立了两个costmap,其中`planner_costmap_ros是用于全局导航的地图,controllercostmap_ros`是用于局部导航用的地图。
通用代价地图
参数文件common_costmap_parameters.yaml,这些参数会影响两个代价地图:1
2
3
4
5
6
7
8
9
10
11
12
13footprint: [[-0.24, -0.22], [-0.24, 0.22], [0.24, 0.22], [0.24, -0.22]]
inflation_radius: 0.05 #before: 1.8 0.3 1.2
obstacle_range: 2.5
raytrace_range: 3.0
cost_scaling_factor: 0.18
observation_sources: scan
scan:
data_type: LaserScan
topic: scan
marking: true
clearing: true
map_type: costmap
footprint: 机器人底盘的轮廓,由一系列二维数据表示,单位为米,每个表示机器人边界的点,逆时针或顺时针方向都可以,轮廓一般是个矩形,机器人中心相当于[0,0]。本参数其实用于表示内切圆和外接圆,它们以一定方式膨胀障碍物以适应机器人。一般为安全起见,本参数比真实轮廓稍微大一些。
robot_radius: 与footprint并列,用于圆形底盘,这个设置就简单多了,就是个半径值,单位米

min_obstacle_height: 传感器读数的最小高度(以米为单位)视为有效。通常设置为地面高度。
obstacle_range: 设置机器人检测障碍物的最大范围,意思是说超过该范围的障碍物,并不进行检测,只有靠近到该范围内才把该障碍物当作影响路径规划和移动的障碍物
raytrace_range: 在机器人移动过程中,实时清除代价地图上的障碍物的最大范围,更新可自由移动的空间数据。假如设置该值为3米,那么就意味着在3米内的障碍物,本来开始时是有的,但是本次检测却没有了,那么就需要在代价地图上来更新,将旧障碍物的空间标记为可以自由移动的空间
全局代价地图
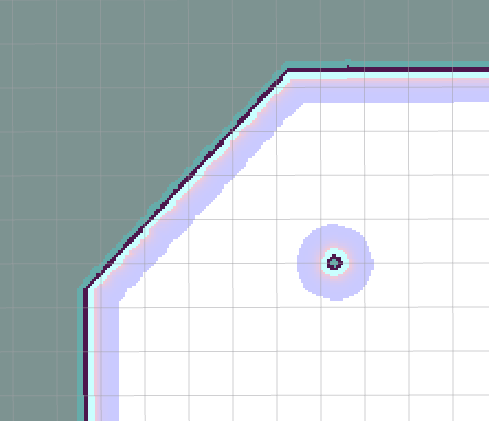
全局地图是从静态地图创建的,使用了后者的数据,只是全局地图将静态地图中的障碍物膨胀化, 依据机器人的足迹半径.
千万注意 pgm 地图文件,边界必须是黑边,而且只给一圈黑色像素不够黑,至少4个,否则不能产生代价地图。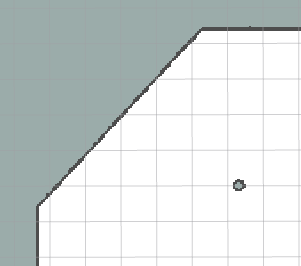
相应的参数文件global_costmap_params.yaml:1
2
3
4
5
6
7
8
9
10
11
12
13global_costmap:
global_frame: map
robot_base_frame: base_link # 或者 base_footprint
update_frequency: 2.0 #before: 5.0
publish_frequency: 2.0 #before 0.5
static_map: true
rolling_window: false # 与static_map相反
transform_tolerance: 0.5 # tf变换允许的最大时间
plugins:
- {name: static, type: "costmap_2d::StaticLayer"}
- {name: obstacles, type: "costmap_2d::VoxelLayer"}
- {name: inflation, type: "costmap_2d::InflationLayer"}
plugins表示你要在costmap加载哪几层,static,obstacles,inflation是不可缺少的。 这些层在common_costmap_parameters.yaml中定义,然后添加到全局和局部代价地图的yaml文件里。如果没有定义,就不能添加到后两者。
全局代价地图对应的话题是/move_base/global_costmap/costmap,注意类型是nav_msgs/OccupancyGrid
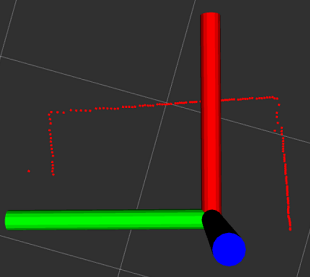
加载代价地图后,可以在Rviz里看到基本参数信息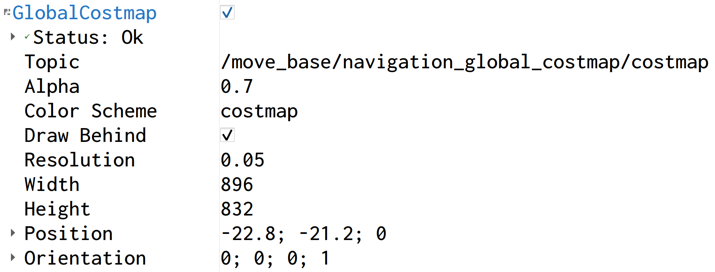
记录一个bug
全局代价地图如果正常生成,理应和地图的大小一样,是2000 x 2000
Costmap2D::worldToMap在刚启动时的打印结果
发导航命令后,代价地图的大小很奇怪地变为200, 原点变为(0,0)1
2
3
4
5
6
7
8
9
10
11Costmap2DR0S transform timeout. Current time: 1687663324.0445, global_pose stamp 321.6492, tolerance: 0.3000
[1687663324.0756730651]: Could not get robot pose, cancelling reconfiguration
[1687663324.6495552631]: MoveBase received move_base goal (48.000000, 58.000000), type: 3
[1687663324]: wx: 46.032079, wy: 46.095481, origin.x: 0.000000, origin_y_: 0.000000
[1687663324]: mx: 920, my: 921 , size_x_: 200, size_y_: 200, resolution.: 0.050000
[1687663324]: wx: 46.032079, wy: 46.095481, start_x_i: 920, start_y_i: 921
[1687663324]: The robot's start position is off the global costmap. Planning will always fail, you sure the robot has been properly localized ?
[1687663324.]: move_base failed to find a plan to point (48.00, 58.00) !
[1687663324.]: wx: 46.032090, wy: 46.095525, start_x_i: 920, start_y_i: 921
局部代价地图
局部规划器用局部代价地图计算出局部路径,局部代价地图是依据机器人的传感器数据创建的,与静态地图无关,它由用户给出宽度和高度。不管机器人怎么运动,它总在局部代价地图的中心,不再这个动态窗口内的障碍信息会drop
相应的参数文件local_costmap_params.yaml:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16local_costmap:
global_frame: odom # 局部代价地图运行的坐标系,也可以是map
robot_base_frame: base_link # 也可以是map
update_frequency: 5.0 # 局部代价地图的更新频率,太大会影响消耗CPU
publish_frequency: 5.0 # 局部代价地图更新的发布频率,如果机器人运动很快,需要增大
static_map: false # 只能是false
rolling_window: true # 只能是true,代价地图在一个rolling window内更新
width: 4 # rolling window的宽度,在rviz显示时会四舍五入
height: 4 # rolling window的高度,在rviz显示时会四舍五入
resolution: 0.02 # rolling window的分辨率
transform_tolerance: 0.5 # tf变换的最大延迟
plugins:
- {name: obstacles_layer, type: "costmap_2d::ObstacleLayer"}
- {name: obstacles, type: "costmap_2d::ObstacleLayer"}
- {name: inflation_layer, type: "costmap_2d::InflationLayer"}
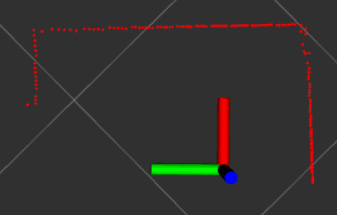
加载局部代价地图成功后
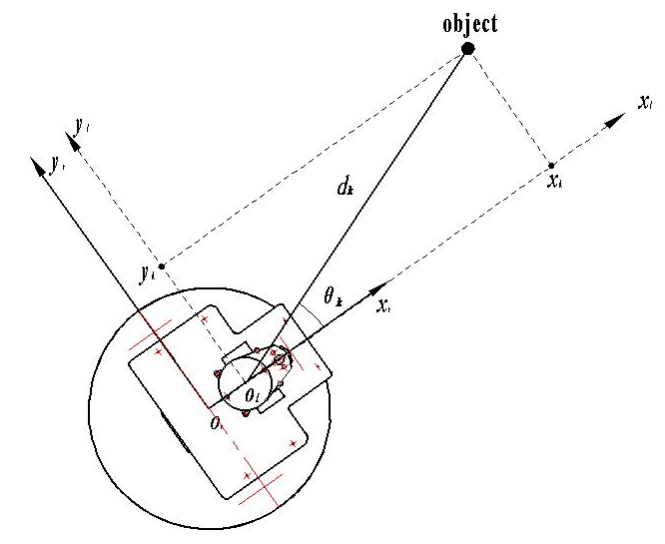
局部代价地图的origin_x_和origin_y_(在costmap_2d.cpp中的成员变量)如图解释,显然随着机器人的运动会变化。
局部代价地图有一个更新的过程:
- 订阅传感器相关主题,根据接受的传感器数据更新代价地图
- 执行标记和清除动作,前者是向代价地图insert障碍信息,后者是从代价地图remove障碍信息。两种动作在障碍层中定义
- 计算每个网格的代价值
- 对每个包含障碍的cell进行障碍膨胀,从每个占据的cell按一定的膨胀半径向外扩张代价值
两个代价地图的设置中,膨胀层要放到所有层的最后,否则全局路径不是贴着膨胀层,而是障碍层。 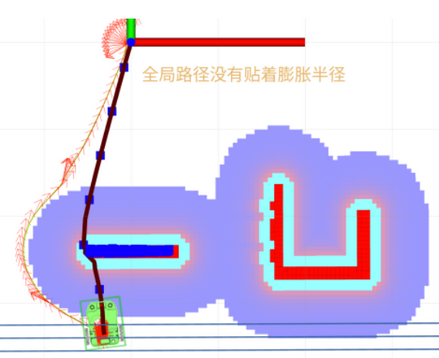
Rviz的map包含3个Color Scheme,costmap, map, raw。若要增加主题,只能写一个Rviz插件或者修改Rviz的源码
参考:代价地图全面分析总结