纯定位的优化改进|激光SLAMCartographer优化
abstract Welcome to my blog, enter password to read.
Read more
landmark的添加残差块|激光SLAMCartographer源码解读
1
2
3
4
5
6
7
8
problem->AddResidualBlock(
    LandmarkCostFunction2D::CreateAutoDiffCostFunction(
        observation, prev->data, next->data),

    new ceres::HuberLoss(huber_scale), 
    prev_node_pose->data(),  next_node_pose->data(), 
    C_landmarks->at(landmark_id).rotation(),
    C_landmarks->at(landmark_id).translation() );

CreateAutoDiffCostFunction

1
2
3
4
5
6
7
8
9
10
11
12
13
14
  static ceres::CostFunction* CreateAutoDiffCostFunction(
      const LandmarkObservation& observation, const NodeSpec2D& prev_node,
      const NodeSpec2D& next_node)
{
    return new ceres::AutoDiffCostFunction<
        LandmarkCostFunction2D,
        6 /* residuals，operator() return的是6维向量 */,
                    // 所估计变量的维度
        3 /* previous node pose variables (x,y,theta) */, 
        3 /* next node pose variables  (x,y,theta)  */,
        4 /* landmark rotation variables  */,
        3 /* landmark translation variables */>(
        new LandmarkCostFunction2D(observation, prev_node, next_node));
}

operator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
  template <typename T>
  bool operator()(const T* const prev_node_pose, const T* const next_node_pose,
                  const T* const landmark_rotation,
                  const T* const landmark_translation,
                  T* const e) const
{
    const std::tuple<std::array<T, 4>, std::array<T, 3>>
        interpolated_rotation_and_translation = InterpolateNodes2D(
            prev_node_pose, prev_node_gravity_alignment_, next_node_pose,
            next_node_gravity_alignment_, interpolation_parameter_);

    const std::array<T, 6> error = ScaleError(
        ComputeUnscaledError(
            landmark_to_tracking_transform_,
            std::get<0>(interpolated_rotation_and_translation).data(),
            std::get<1>(interpolated_rotation_and_translation).data(),
            landmark_rotation, landmark_translation),
        translation_weight_, rotation_weight_);

    std::copy(std::begin(error), std::end(error), e);
    return true;
}

ComputeUnscaledError

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
template <typename T>
static std::array<T, 6> ComputeUnscaledError(
    const transform::Rigid3d&  relative_pose, 
    const T* const start_rotation,  const T* const start_translation, 
    const T* const end_rotation,    const T* const end_translation )
{
	// 四元数共轭，在这里就是逆
  const Eigen::Quaternion<T> R_i_inverse( start_rotation[0],
                                         -start_rotation[1],
                                         -start_rotation[2],
                                         -start_rotation[3] );
    // 平移的差
  const Eigen::Matrix<T, 3, 1> delta(end_translation[0] - start_translation[0],
                                     end_translation[1] - start_translation[1],
                                     end_translation[2] - start_translation[2]);
  const Eigen::Matrix<T, 3, 1> h_translation = R_i_inverse * delta;

  const Eigen::Quaternion<T> h_rotation_inverse =
      Eigen::Quaternion<T>(end_rotation[0], -end_rotation[1], 
                          -end_rotation[2], -end_rotation[3]) *
      Eigen::Quaternion<T>(start_rotation[0], start_rotation[1],
                           start_rotation[2], start_rotation[3]);

  const Eigen::Matrix<T, 3, 1> angle_axis_difference =
      transform::RotationQuaternionToAngleAxisVector(
          h_rotation_inverse * relative_pose.rotation().cast<T>());

  return {  {T(relative_pose.translation().x()) - h_translation[0],
             T(relative_pose.translation().y()) - h_translation[1],
             T(relative_pose.translation().z()) - h_translation[2],
           angle_axis_difference[0], 
           angle_axis_difference[1],
           angle_axis_difference[2]}  };
}

relative_pose 是 landmark_to_tracking_transform，landmark和tracking坐标系的相对位姿，在SensorBridge::HandleLandmarkMessage中获得

landmark作为独立变量进入Pose Graph的稀疏优化，它增加的优化维度是 landmarks个数 * 每个landmark的参数个数，不要使用太多landmark

ScaleError一看就是残差乘以权重

1
2
3
4
5
6
7
8
9
10
11
template <typename T>
std::array<T, 3> ScaleError( const std::array<T, 3>& error,
                             double translation_weight,
                             double rotation_weight )
{
  return {{
      error[0] * translation_weight,
      error[1] * translation_weight,
      error[2] * rotation_weight
  }};
}

landmark的后端处理|激光SLAMCartographer源码解读

加入landmark后，Pose Graph有了不同的node和edge，也就是landmark也作为node，landmark-pose之间的 edge是新的一种edge，即在pose对landmark的观测

1
2
3
4
5
6
7
8
9
10
11
12
13
struct LandmarkNode {
    struct LandmarkObservation {
      int trajectory_id;
      common::Time time;
      transform::Rigid3d landmark_to_tracking_transform;
      double translation_weight;
      double rotation_weight;
    };
    // 同一时刻，可能观测到多个landmark数据
    std::vector<LandmarkObservation> landmark_observations;
    absl::optional<transform::Rigid3d> global_landmark_pose;
    bool frozen = false;
  };

landmark是应用于后端，不是实时的，应当调大权重让carto更相信它的结果

添加数据部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void PoseGraph2D::AddLandmarkData(int trajectory_id,
                                  const sensor::LandmarkData& landmark_data)
{
  AddWorkItem([=]() LOCKS_EXCLUDED(mutex_) {
    absl::MutexLock locker(&mutex_);
    if (CanAddWorkItemModifying(trajectory_id)) {
      for (const auto& observation : landmark_data.landmark_observations)
      {
      	          			// initial landmark_nodes
          // const transform::Rigid3d global_pose =
          // observation.landmark_to_map_transform;
      #if 0
      data_.landmark_nodes的类型是 std::map<std::string /* landmark ID */, PoseGraphInterface::LandmarkNode>
      #endif
        data_.landmark_nodes[observation.id].landmark_observations.emplace_back(
            PoseGraphInterface::LandmarkNode::LandmarkObservation{
                trajectory_id, landmark_data.time,
                observation.landmark_to_tracking_transform,
                observation.translation_weight, observation.rotation_weight} );

          // data_.landmark_nodes[observation.id].global_landmark_pose = global_pose;
      }
    }
    // optimization_problem_->new_landmark_add_ = true;
    return WorkItem::Result::kDoNotRunOptimization;
  });
}

这里就是把观测到的landmark信息都保存到data_.landmark_nodes，最后返回的标识也是不优化

后端优化的流程和其他传感器数据一样:
PoseGraph2D::HandleWorkQueue —— PoseGraph2D::RunOptimization —— OptimizationProblem2D::Solve(data_.constraints, GetTrajectoryStates(), data_.landmark_nodes) —— AddLandmarkCostFunctions(landmark_nodes, node_data_, &C_nodes, &C_landmarks, &problem, options_.huber_scale() )

OptimizationProblem2D::Solve部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
  std::set<int> frozen_trajectories;
  for (const auto& it : trajectories_state)
  {
    if (it.second == PoseGraphInterface::TrajectoryState::FROZEN)
    {
      frozen_trajectories.insert(it.first);
    }
  }

  ceres::Problem::Options problem_options;
  ceres::Problem problem(problem_options);

  // Set the starting point.  TODO(hrapp): Move ceres data into SubmapSpec.
  // ceres需要的是double指针，std::array 能转成原始指针的形式
  MapById<SubmapId, std::array<double, 3>> C_submaps;
  MapById<NodeId, std::array<double, 3>> C_nodes;
  std::map<std::string, CeresPose> C_landmarks;
  bool first_submap = true;


  // 将需要优化的  子图位姿  设置为优化参数
  for (const auto& submap_id_data : submap_data_) {
    // submap_id的轨迹是否是冻结的
    const bool frozen =
        frozen_trajectories.count(submap_id_data.id.trajectory_id) != 0;
        // 将子图的global_pose放入 C_submaps
    C_submaps.Insert(submap_id_data.id,
                     FromPose(submap_id_data.data.global_pose));
    // c++11中，std::array::data()返回指向数组对象第一个元素的指针
    problem.AddParameterBlock(C_submaps.at(submap_id_data.id).data(), 3);

    // 第一个子图或冻结，不优化子图位姿。 也就是不优化初值
    if (first_submap || frozen) {
      first_submap = false;
      // Fix the pose of the first submap or all submaps of a frozen
      // trajectory.
      problem.SetParameterBlockConstant(C_submaps.at(submap_id_data.id).data());
    }
  }

  // 需要优化的  节点位姿  设置为优化参数，与上面的子图优化大致相同
  for (const auto& node_id_data : node_data_)
  {
    const bool frozen =
        frozen_trajectories.count(node_id_data.id.trajectory_id) != 0;
    C_nodes.Insert(node_id_data.id, FromPose(node_id_data.data.global_pose_2d));
    problem.AddParameterBlock(C_nodes.at(node_id_data.id).data(), 3);
    if (frozen)
    {
      // 这里的第一个节点也要参与优化，跟子图的不同了
      problem.SetParameterBlockConstant(C_nodes.at(node_id_data.id).data());
    }
  }
				/* ...... */
// 第2种残差：landmark与landmark数据插值出来的节点相对位姿的差值
AddLandmarkCostFunctions(landmark_nodes, node_data_, 
						&C_nodes, &C_landmarks,
                        &problem, options_.huber_scale()  );

landmark数据 与 通过2个节点位姿插值出来的相对位姿 的差值作为残差项

AddLandmarkCostFunctions

最外层两个循环是遍历landmark节点和遍历每个节点的观测，也就是说可能会同时看到多个landmark。直接看循环里面的内容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
const std::string& landmark_id = landmark_node.first;
// 轨迹中第一个 node_data
const auto& begin_of_trajectory =
    node_data.BeginOfTrajectory(observation.trajectory_id);
// 如果 landmark observation was made before the trajectory was created
if (observation.time < begin_of_trajectory->data.time) {
    continue;
}
/* 以下语句Find the trajectory nodes before and after the landmark observation */

// 找到在landmark观测时间后的第一个节点
auto next = 
    node_data.lower_bound(observation.trajectory_id, observation.time);
/*  The landmark observation was made, but the next trajectory node has
    not been added yet. 即next已经是轨迹最后一个节点  */
if (next == node_data.EndOfTrajectory(observation.trajectory_id)  ) {
    continue;
}
// 如果是刚开始的node data
if (next == begin_of_trajectory) {
  next = std::next(next);
}
// 这里的pre配合next是为了获取两个位置，找到landmark观测时间的前一个节点
auto prev = std::prev(next);

// 根据两个索引，获取两个节点位姿
// Add parameter blocks for the landmark ID if they were not added before
std::array<double, 3>* prev_node_pose = &C_nodes->at(prev->id);
std::array<double, 3>* next_node_pose = &C_nodes->at(next->id);

根据landmark观测的时间，找到观测前后的节点，获取位姿

1
2
3
4
5
6
7
8
9
// 如果landmark_id 不存在于 C_landmarks，
if (!C_landmarks->count(landmark_id)){
  // landmark如果已经优化，则 global_landmark_pose 有值
  // 否则根据时间插值计算一个位姿
  const transform::Rigid3d starting_point =
      landmark_node.second.global_landmark_pose.has_value()
          ? landmark_node.second.global_landmark_pose.value()
          : GetInitialLandmarkPose(observation, prev->data, next->data,
                                   *prev_node_pose, *next_node_pose);

开始C_landmarks当然为空，只有在优化完成后，这里才存在，即 RunOptimization 的最后会添加: data_.landmark_nodes[landmark.first].global_landmark_pose = landmark.second;，顺着上面的调用路线就能发现

GetInitialLandmarkPose

这里用了一堆数据类型转换，以及四元数、旋转向量、欧拉角之间的转换。还重新实现了slerp函数SlerpQuaternions，因为Eigen的slerp与Ceres的不兼容。
过程


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  C_landmarks->emplace(
      landmark_id,
      // 四元数不支持广义加法，使用QuaternionParameterization 
      CeresPose(starting_point, nullptr /* translation_parametrization */,
                absl::make_unique<ceres::QuaternionParameterization>(),
                problem)  );

  // Set landmark constant if it is frozen. 不参与优化
  // 这里容易记不清，frozen 定义在  struct LandmarkNode
  if (landmark_node.second.frozen) {
    problem->SetParameterBlockConstant(
        C_landmarks->at(landmark_id).translation());

    problem->SetParameterBlockConstant(
        C_landmarks->at(landmark_id).rotation());
  }
}

CeresPose的构造函数里就两行

1
2
3
4
problem->AddParameterBlock(data_->translation.data(), 3,
                         translation_parametrization.release());
problem->AddParameterBlock(data_->rotation.data(), 4,
                         rotation_parametrization.release());

对于平移，无需ceres::LocalParameterization


添加残差块

1
2
3
4
5
6
7
8
problem->AddResidualBlock(
    LandmarkCostFunction2D::CreateAutoDiffCostFunction(
        observation, prev->data, next->data),

    new ceres::HuberLoss(huber_scale), 
    prev_node_pose->data(),  next_node_pose->data(), 
    C_landmarks->at(landmark_id).rotation(),
    C_landmarks->at(landmark_id).translation() );

if (!C_landmarks->count(landmark_id))已经结束，添加残差块。

Solve 和 RunOptimization 的最后处理

Solve的最后

1
2
3
4
for (const auto& C_landmark : C_landmarks) {
	// first 是 landmark_id
	landmark_data_[C_landmark.first] = C_landmark.second.ToRigid();
}

这个C_landmarks还是上面那个，ToRigid()当然是优化后的landmark全局位姿了

在RunOptimization的最后

1
2
3
4
5
6
// 遍历成员变量 landmark_data_，它在 Solve 函数的最后赋值
for (const auto& landmark : optimization_problem_->landmark_data() )
{
	 // first 是 landmark_id
  data_.landmark_nodes[landmark.first].global_landmark_pose = landmark.second;
}

optimization_problem_->landmark_data()返回的就是上面的landmark_data_，说白了，这里就是把优化后的landmark数据从OptimizationProblem2D层传回PoseGraph2D层

landmark的前端处理|激光SLAMCartographer源码解读

landmark就是添加了一个观测，让定位更鲁棒。如果观测是空的，应当发布空的 landmark messages to unblock the queue. 对于fixed frame poses (GPS)也适用。

前端的处理

node.cc 层

1
2
3
4
// landmark_poses_list 话题
  landmark_poses_list_publisher_ =
      node_handle_.advertise<::visualization_msgs::MarkerArray>(
          kLandmarkPosesListTopic, kLatestOnlyPublisherQueueSize);

发布话题：

1
2
3
4
5
6
7
8
void Node::PublishLandmarkPosesList(const ::ros::WallTimerEvent& unused_timer_event)
{
  if (landmark_poses_list_publisher_.getNumSubscribers() > 0)
  {
      absl::MutexLock lock(&mutex_);
      landmark_poses_list_publisher_.publish(map_builder_bridge_.GetLandmarkPosesList() );
  }
}

处理传感器数据

1
2
3
4
5
6
7
8
9
10
11
void Node::HandleLandmarkMessage(
    const int trajectory_id, const std::string& sensor_id,
    const cartographer_ros_msgs::LandmarkList::ConstPtr& msg)
{
  absl::MutexLock lock(&mutex_);
  if (!sensor_samplers_.at(trajectory_id).landmark_sampler.Pulse()) 
      return;
  CHECK(msg->landmarks.size() != 0) << "No Landmarks !";

  map_builder_bridge_.sensor_bridge(trajectory_id)->HandleLandmarkMessage(sensor_id, msg);
}

sensor_bridge.cc 层

用到的类型

1
2
3
4
5
6
7
8
9
10
11
12
struct LandmarkData {
  common::Time time;
  std::vector<LandmarkObservation> landmark_observations;
};

struct LandmarkObservation
{
  std::string id;
  transform::Rigid3d landmark_to_tracking_transform;
  double translation_weight;
  double rotation_weight;
};

如果是二维码，就可以将识别到的ID传进去，landmark的观测是相对于 tracking 坐标系的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void SensorBridge::HandleLandmarkMessage(
    const std::string& sensor_id,
    const cartographer_ros_msgs::LandmarkList::ConstPtr& msg)
{
  auto landmark_data = ToLandmarkData(*msg);
  auto tracking_from_landmark_sensor = tf_bridge_.LookupToTracking(
      landmark_data.time, CheckNoLeadingSlash(msg->header.frame_id));
  // 把相机对landmark的观测，转换到 tracking 坐标系
  if (tracking_from_landmark_sensor != nullptr)
  {
      for (auto& observation : landmark_data.landmark_observations)
      {
        observation.landmark_to_tracking_transform =
            *tracking_from_landmark_sensor *
            observation.landmark_to_tracking_transform;
      }
  }
  // 进入传感器数据融合阶段
  trajectory_builder_->AddSensorData(sensor_id, landmark_data);
}

简单的类型转换而已

1
2
3
4
5
6
7
8
9
10
11
12
13
14
LandmarkData ToLandmarkData(const LandmarkList& landmark_list)
{
    LandmarkData landmark_data;
    landmark_data.time = FromRos(landmark_list.header.stamp);
    for (const LandmarkEntry& entry : landmark_list.landmark)
    {
        landmark_data.landmark_observations.push_back(
        {entry.id, ToRigid3d(entry.tracking_from_landmark_transform),
         entry.translation_weight, 10, entry.type});
         //LOG(INFO) << "find landmark x: " << entry.tracking_from_landmark_transform.position.x;
         //LOG(INFO) << "find landmark y: " << entry.tracking_from_landmark_transform.position.y;
    }
    return landmark_data;
}

数据融合阶段

CollatedTrajectoryBuilder类

1
2
3
4
5
6
7
8
9
10
11
12
void AddSensorData(const std::string& sensor_id,
                   const sensor::LandmarkData& landmark_data) override
{
    if (collate_landmarks_)
    {
      AddData(sensor::MakeDispatchable(sensor_id, landmark_data));
      return;
    }
    // wrapped_trajectory_builder_ 赋值在 CollatedTrajectoryBuilder 构造函数
    // 应当为map_builder_->GetTrajectoryBuilder(trajectory_id)
    wrapped_trajectory_builder_->AddSensorData(sensor_id, landmark_data);
}

  • collate_landmarks的设置问题

在CollatedTrajectoryBuilder的构造函数里体现，注意设置为on或off，不是true, false

1
2
3
4
5
if (sensor_id.type == SensorId::SensorType::LANDMARK &&
    !collate_landmarks_)
{
    continue;
}

如果提供landmark的观测不低于10 Hz，那么可以设置TRAJECTORY_BUILDER.collate_landmarks = on. Cartographer将deterministically运行(对于给定的bag, 使用offline node每次获得的结果是一样的). 如果collate_landmarks = off， landmark observations将跳过sensor queue (so they do not block it if they are sparse) and are injected directly into the pose graph, which is not deterministic.

但是看到另一种说法，在 #1224更新版本，作者提出如果有landmark，collate_landmarks就要为 false。这个再观察

接下来进入GlobalTrajectoryBuilder

1
2
3
4
5
void AddSensorData(const std::string& sensor_id,
                   const sensor::LandmarkData& landmark_data) override
{
   pose_graph_->AddLandmarkData(trajectory_id_, landmark_data);
}

这里可以看到landmark数据直接进后端，前端没有它的事了

旷视的CamLaserCalibraTool|激光SLAM其他

看到网上有些人说标定结果不错，但我试了很多次，开始还能出运行结果，但是和实际差太多，后来换了个相机，几乎不能运行成功了。kalibr图案、棋盘格、apriltag都试过了，代码调试了很多地方，都不顺利，看github也有很多issue未解决，先搁置了

配置

laser_filter的配置filter.yaml修改如下

1
2
3
4
5
6
7
8
9
10
11
12
scan_filter_chain:
- name: angle
  type: laser_filters/LaserScanAngularBoundsFilter
  params:
    lower_angle: -0.6
    upper_angle: 0.6
- name: range
  type: laser_filters/LaserScanRangeFilter
  params:
    use_message_range_limits: false
    lower_threshold: 0.5
    upper_threshold: 2.2

配置文件中的tag_spacing = 0.3并不是tag_spacing的实际距离大小，而是比例：8.8x0.3=2.64，因此这里的tag_spacing是一个固定值为0.3，不用修改！

录制bag要包括雷达scan和图像

1
rosbag record scan_filtered /camera_node/image_raw -O pinhole.bag

roslaunch lasercamcal_ros kalibra_apriltag.launch会把检测到每一帧中的april的信息保存到apriltag_pose.txt文件中，作者录制的数据包有1527 msgs，最终也是每一帧都检测到了，我录制的bag有时会有一些帧检测不到，似乎不是什么问题。

作者也是没有对录制的包直接做数据时间同步的，相机的帧率大概是2D激光雷达的二倍

移动标定板

要求是：标定板在激光正前方120°范围内，并且激光前方2m范围内只存在一个连续的直线线段，所以请在空旷的地方采集数据，不然激光数据会提取错误。需要充分旋转 roll 和 pitch。更直白一点，假设在长方形的标定板中心画了个十字线，那请绕着十字线的两个轴充分旋转，比如绕着竖轴旋转，然后还要绕着横轴旋转。在运行offline程序时，程序会将认为正确的直线会显示为红色。

激光线要能落在标定板上。不断调整标定板姿态，每换一个姿态(绕Roll, Pitch, Yaw旋转，移动位置)，请保持静止 2 秒以上，采集 10 个姿态左右的数据（当然越多越好）。用 rosbag 记录所有的图像和激光数据， 标定工具会自动检测你保持静止时刻的数据，并用来标定。

1
2
3
4
5
6
7
--------- start AutoGetLinePts ---------
id_left: 182, dist left: 1414
id_right: 0, dist right: 1

currentPt: 0  nextPt: 3
d1: 1.085,  d2: 1414.21
d2: 1000  1000

这里的1000,1414其实就是对应scan的range为nan的情况，在if(d1 < range_max && d2 < range_max)里过滤掉了，不用管了

失败的情况

Valid Calibra Data too little

运行roslaunch lasercamcal_ros calibra_offline.launch，结果OpenCV窗口的标定板对应线段不是红色，也没有results.yaml
终端出现Valid Calibra Data too little

查代码发现points = AutoGetLinePts(Points);没有检测到直线。接着查发现问题在selectScanPoints.cpp中的

1
2
3
4
5
6
7
8
9
 // 至少长于 20 cm, 标定板不能距离激光超过2m, 标定板上的激光点超过 50 个
if(dist.head(2).norm() > 0.2
   && points.at(seg.id_start).head(2).norm() < 2
   && points.at(seg.id_end).head(2).norm() < 2
   && seg.id_end-seg.id_start > 50   ) 
{
    seg.dist = dist.head(2).norm();
    segs.push_back(seg);
}

有时第一项和最后一项不符合；有时第一项符合，但中间两项又不符合；第四项大部分情况是3. 常见的四个参数如下
1
2
3
4
5
6
7
8
9
0.100479
1.294
1.218
3

0.201422
2.357
2.513
3

看来是不符合只有一个连续直线这条要求，后来又试了一次，虽然出现了红色直线，但是错的
错误的结果

最后终于明白了，源码中的参数都是作者的雷达相关的，需要根据自己雷达调整。int delta = 80/0.3;的两个参数根据雷达角分辨率调整。50降为18，这样就成功了，int skip = 3;也可能要调整。

但是常常不管怎么调参数，仍然可用数据太少

越界

运行calibra_offline.launch得到的bug

1
2
3
4
Load apriltag pose size: 582
terminate called after throwing an instance of 'std::out_of_range'
  what():  vector::_M_range_check: __n (which is 18446744073709551615) >= this->size() (which is 57)
[lasercamcal_ros-1] process has died

有时连录几次bag，都出现这种情况，估计是某个地方在for循环里push_back导致

结果不可观

计算初值阶段

1
2
3
4
5
6
7
8
9
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 Notice Notice Notice: system unobservable !!!!!!!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

------- Closed-form solution Tlc: -------
   1    0    0 -nan
   0    1    0 -nan
   0    0    1  nan
   0    0    0    1

tf(三) lookTransform和齐次变换矩阵的关系推导

建立tf树 A—->B—->C，求 C—->A变换

1
2
rosrun tf static_transform_publisher 0.169, 0.035, -0.125,   -1.57, 0, -1.57  A  B 100
rosrun tf static_transform_publisher   0,   0.015,     0,    -1.57, 0, -1.57  B  C 100

平时使用的tf是tf::Transformer::lookupTransform(target_frame, source_frame)，表示的是 source_frame ---> target_frame的变换，获得的位姿关系是子在父坐标系中，所以是lookupTransform("A", "B")，根据《SLAM十四讲》63页的表示方法，写成
，也就是父子顺序。 因此 C—->A变换是

代码

CMake关键部分：

1
2
3
4
5
6
7
find_package(catkin REQUIRED COMPONENTS
  eigen_conversions
  roscpp
  tf
  pcl_ros
)
find_package(PCL 1.3 REQUIRED COMPONENTS common io)

c++关键部分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <ros/ros.h>
#include <Eigen/Dense>
#include <tf/transform_broadcaster.h>
#include <tf/message_filter.h>
#include <tf/transform_listener.h>
#include <pcl_conversions/pcl_conversions.h>
#include <pcl_ros/transforms.h>

tf::TransformListener listener;

ros::Rate rate(10.0);
while (node.ok())
{
	//创建一个StampedTransform对象存储变换结果数据
	tf::StampedTransform ab;
	tf::StampedTransform bc;
	tf::StampedTransform tfAC;
	try{
	    listener.lookupTransform("A", "B",
	                             ros::Time(0), ab);
	    listener.lookupTransform("B", "C",
	                             ros::Time(0), bc);
	    listener.lookupTransform("A", "C",
	                             ros::Time(0), tfAC);
	    // 输出 lookupTransform 输出的 C--->A 变换
	    cout << "X: "<< tfAC.getOrigin().getX() << " Y: "<< tfAC.getOrigin().getY()
	            <<"  Z: "<< tfAC.getOrigin().getZ()<< endl;
	    cout << "quaternion: "<< tfAC.getRotation().x() <<" " << tfAC.getRotation().y()<<
	            " " << tfAC.getRotation().z() << " " << tfAC.getRotation().w() << endl;

    Eigen::Matrix4f AB, BC, AC;
    // 使用 pcl_ros 直接得到 4x4的齐次变换矩阵
    pcl_ros::transformAsMatrix(ab, AB);   
    pcl_ros::transformAsMatrix(bc, BC);
    std::cout << "AB:"  <<std::endl;
    std::cout << AB  <<std::endl;
    std::cout << "BC:"  <<std::endl;
    std::cout << BC  <<std::endl;
    std::cout << "AC:"  <<std::endl;
    AC = AB * BC;
    std::cout << AC  <<std::endl;
    cout << "-------------------------------------" << endl;
  }
  catch (tf::TransformException &ex) {
    ROS_ERROR("%s",ex.what());
    ros::Duration(1.0).sleep();
    continue;
  }
}

可以看到AC的右侧平移部分和tfAC.getOrigin()部分相同

tf::lookupTransform的源码一直追溯到tf2_ros::Buffer::lookupTransform，源码在f2/src/buffer_core.cpp，注意其中的accum函数和BufferCore::walkToTopParent函数

tf_eigen

tf_eigen.h提供了不少很有用的函数，用于tf和Eigen之间的矩阵和向量互相转换。使用前

1
2
3
4
find_package(catkin REQUIRED COMPONENTS
  eigen_conversions
  tf_conversions
)

头文件#include <tf_conversions/tf_eigen.h>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// Converts an Eigen Quaternion into a tf Matrix3x3.
void  tf::matrixEigenToTF (const Eigen::Matrix3d &e, tf::Matrix3x3 &t)
  // Converts a tf Matrix3x3 into an Eigen Quaternion.
void  tf::matrixTFToEigen (const tf::Matrix3x3 &t, Eigen::Matrix3d &e)

  // Converts an Eigen Affine3d into a tf Transform.
void  tf::poseEigenToTF (const Eigen::Affine3d &e, tf::Pose &t)
  // Converts a tf Pose into an Eigen Affine3d.
void  tf::poseTFToEigen (const tf::Pose &t, Eigen::Affine3d &e)
  
// Converts an Eigen Quaternion into a tf Quaternion.
void  tf::quaternionEigenToTF (const Eigen::Quaterniond &e, tf::Quaternion &t)
  // Converts a tf Quaternion into an Eigen Quaternion.
void  tf::quaternionTFToEigen (const tf::Quaternion &t, Eigen::Quaterniond &e)
  
  // Converts an Eigen Affine3d into a tf Transform.
void  tf::transformEigenToTF (const Eigen::Affine3d &e, tf::Transform &t)
  // Converts a tf Transform into an Eigen Affine3d.
void  tf::transformTFToEigen (const tf::Transform &t, Eigen::Affine3d &e)

  // Converts an Eigen Vector3d into a tf Vector3.
void  tf::vectorEigenToTF (const Eigen::Vector3d &e, tf::Vector3 &t)
   // Converts a tf Vector3 into an Eigen Vector3d.
void  tf::vectorTFToEigen (const tf::Vector3 &t, Eigen::Vector3d &e)
标定雷达和相机的外参|激光SLAM其他

粗标定

realsense和雷达外参的粗标定，也就是laser坐标系和camera_color_optical_frame之间的相对位姿，但如果realsense是低着头，竖直和横向的相对位姿的测量误差就大了。

使用realsense检测贴在墙上的二维码，获得距离，同时使用雷达检测到墙的距离，让雷达尽量正对二维码位置。

雷达到前方距离: 1.288，对应realsense的z值: 1.119，二者差 0.169
用直尺测量高度的差: 0.125
横向: realsense在雷达左侧 0.035

如果laser为父坐标系，二者的变换矩阵为

但realsense的坐标系体系是 camera_link —-> camera_color_frame —-> camera_color_optical_frame，其中

1
2
3
4
5
camera_link camera_color_optical_frame
- Translation: [0.000, 0.015, 0.000]
- Rotation: in Quaternion [-0.498, 0.502, -0.498, 0.502]
            in RPY (radian) [-1.571, 0.008, -1.570]
            in RPY (degree) [-89.992, 0.476, -89.975]

所以不能直接建立laser坐标系和camera_color_optical_frame的父子关系，要建立laser和camera_link的。

使用变换矩阵的计算，已知 ， 。 计算

结果转为tf格式，应当为 <node pkg="tf" type="static_transform_publisher" name="laser_camera_broadcaster" args="0.169 0.02 -0.125 0 0 0 laser camera_link 100"/>

向量，平面和坐标系变换|数学基础

向量

  • 标准化后的向量点乘得到的值为夹角的余弦。如果得到 -1, 0, -1，便可知道两个向量方向的关系是相反, 垂直, 相同

  • 向量叉乘后得到的向量和原先两个向量垂直，也就是法向量

  • 向量叉乘后得到的向量的模，其值为两个向量构成的三角形的面积的二倍。

  • 叉乘的一些性质


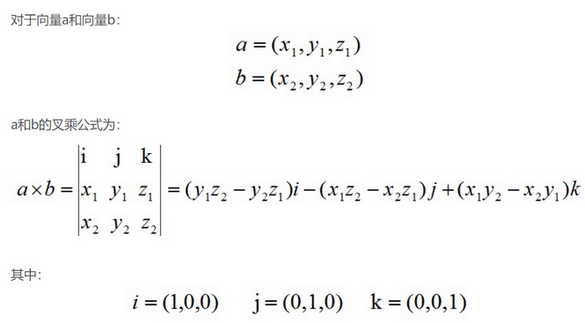
用行列式的表示方法观察，不用计算就能看出前三条。

平面的一般式

高中学过的表示方法为 ，法向量为 。这里涉及到了归一化问题，两边可以乘以系数，还是同一个平面，也可以说法向量是不唯一的。但如果给出了一般式 ，就说法向量为

空间内一点 到平面的距离是 ，如果已经归一化，那么分母就是 1

法向量可以看做平面上两个向量的叉乘。

法向量 * 距离形式

N为法向量(1x3的向量)，那么[N, d]或者(N | d)为 1x4 的向量，其中d为平面到原点的距离。

旋转问题

现在平面的表示形式(无论哪种)都是基于坐标系A，另有一个坐标系B，从B到A的变换矩阵是M(4x4)，那么平面在坐标系B下的表示形式是什么？

向量 ，注意不是法向量，平面上一点为 ，那么 ，经过变换后，点v变成了 ，那么有 ，也就有，因此可得 ，M矩阵的逆根据《SLAM十四讲》的公式3.13可以直接写出，最后根据 写成一般式

感觉这样推导并不严谨，但可以这样理解。

参考：OpenGL Normal Vector Transformation

Ceres(三) 解析求导|SLAM工具

最常见的一个例子是 链接，不再复制粘贴

还是之前的曲线拟合问题： ，如果改用解析求导，需要构建一个继承CostFunction的类。核心函数是bool CostFunction: :Evaluate(double const *const *parameters, double *residuals, double **jacobians)，计算残差向量和雅可比矩阵

  • parameters: parameters是一个大小为CostFunction::parameter_block_sizes_.size()(输入参数块的数量和大小)的数组，parameters[i]是一个大小为parameter_block_sizes_[i]的数组，其中包含CostFunction所依赖的第i个参数块。parameters不会为nullptr

  • residuals: 是一个大小为num_residuals_(输出残差的个数)的数组。residuals也不会为nullptr

  • jacobians: 是一个大小为CostFunction::parameter_block_sizes_.size()的数组。如果jacobians是nullptr，用户只需要计算残差

  • jacobians[i]: 是一个大小为 num_residuals x parameter_block_sizes_[i] 的行数组，如果jacobians[i]不为nullptr，用户需要计算关于parameters[i]的残差向量的雅可比矩阵，并将其存储在这个数组中，即

如果jacobians为nullptr，通常我们只需要在Evaluate函数中实现residuals的计算，jacobians后面可以通过Ceres提供的自动求导（数值求导）替代，否则，还需要在Evaluate函数中实现jacobians的计算

如果parameters大小和residuals大小在编译时是已知的，就可以使用SizeCostFunction，该函数可以将paramters大小和residuals大小设置为模板参数，用户只需要在使用的时候给模板参数赋值就可以

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 模板参数依次为： number of residuals,  first parameter的维度
class MyCostFun : public SizedCostFunction<1, 1, 1, 1>
{
    public:
		MyCostFun(double x, double y):
			m_x(x), m_y(y){}
   virtual bool Evaluate(double const* const* parameters,
		      	 double* residuals,
			 double** jacobians) const
   {
       double a = parameters[0][0];
       double b = parameters[0][1];
       double c = parameters[0][2];
       residuals[0] = m_y - exp(a*m_x*m_x + b*m_x + c);

		if (jacobians != NULL && jacobians[0] != NULL)
		{
		    jacobians[0][0] = -exp(a*m_x*m_x + b*m_x + c)* m_x * m_x;
		    jacobians[0][1] = -exp(a*m_x*m_x + b*m_x + c)* m_x;
		    jacobians[0][2] = -exp(a*m_x*m_x + b*m_x + c);

		}
		return true;
   }
   protected:
	double m_x;
    double m_y;
};

拟合 时，使用SizedCostFunction<1, 2>，只计算雅格比jacobians[0][0] 和 jacobians[0][1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int main(int argv, char** argc)
{
    ros::init(argv, argc, "test_ceres");
    ros::NodeHandle nh;
    // 真实值
	double a = 1.0, b = 2.0, c = 1.0;

	// 生成带有噪声的模拟数据
	vector<double> x_data, y_data;
	int N = 240;  // 数据数量
	double w_sigma = 1.0;  // 高斯标准差
	cv::RNG  rng;
	for(unsigned int i =0; i<N; i++)
	{
		double x = i/100.0;
		x_data.push_back(x);
		y_data.push_back(exp(a*x*x + b*x + c) + rng.gaussian(w_sigma)  );
	}
	// 作为初值
	a = 0.0;
	b = 0.0;
	c = 0.0;
	Problem problem;
	for(unsigned int i=0; i<N; i++)
	{
		CostFunction* cost_func = new MyCostFun(x_data[i], y_data[i]);
		problem.AddResidualBlock(cost_func, nullptr, &a, &b, &c);
	}
	Solver::Options option;
	option.minimizer_progress_to_stdout = true;

	Solver::Summary summary;
	Solve(option, &problem, &summary);
	cout << summary.BriefReport() << endl <<endl;
	cout << "a: "<< a <<"  b: "<< b << "  c: "<< c <<endl;

    return 0;
}

一开始我设置代价函数的模板为SizedCostFunction<1, 3>，结果运行报错： [problem_impl.cc:286] Check failed: num_parameter_blocks == cost_function->parameter_block_sizes().size() (3 vs. 1)

问题在于parameter_block_sizes只有1，而我们需要3，也就是对应abc三个参数。读SizedCostFunction源码发现，模板定义为template <int kNumResiduals, int... Ns>，构造函数只有两行

1
2
set_num_residuals(kNumResiduals);
*mutable_parameter_block_sizes() = std::vector<int32_t>{Ns...};

因此从第2个模板参数开始，有几个参数就对应parameter_block_sizes，改为SizedCostFunction<1, 1, 1, 1>

(零) 安装cartographer|激光SLAMCartographer原理和配置

cartographer的安装非常复杂，尤其是proto脚本和各种依赖项，如果一次不成功，最好把proto或其他依赖库彻底删除重来，越改可能越乱，再也装不好了。

ros2的carto好像还是非常早期的版本，一些参数都不支持，先不必使用

安装过程的问题

下载protobuf很可能失败，只好手动下载: git clone https://github.com/google/protobuf.git

小强编译cartographer更新的lib文件在/home/xiaoqiang/Documents/ros/devel/lib/cartographer_ros

gtest问题

编译cartographer报错gtest

1
2
/usr/src/gtest/src/gtest.cc:1897:10: error: type ‘const class testing::internal::scoped_ptr<testing::internal::GTestFlagSaver>’ argument given to ‘delete’, expected pointer
   delete gtest_flag_saver_;

估计是gtest的版本不兼容导致，从github上下载编译google-test，注意修改CMake支持c++14，否则连从github直接下载的源码编译也报错：

然后编译cartographer时，把几个重要的CMakeLists.txt也加上c++14的支持，否则所有的测试文件(以test.cc结尾的文件)编译都会出错

缺少liborocos-kdl库文件

默认的版本是1.3.2，这是下载地址

缺FindLuaGoogle

报错：

1
2
3
Could NOT find Lua (missing: LUA_LIBRARIES LUA_INCLUDE_DIR) 
CMake Error at cmake/modules/FindLuaGoogle.cmake:217 (MESSAGE):
  Did not find Lua >= 5.2

解决： sudo apt-get install lua5.2 lua5.2-dev

absl库的问题

cartographer新版本要先安装abseil，否则报错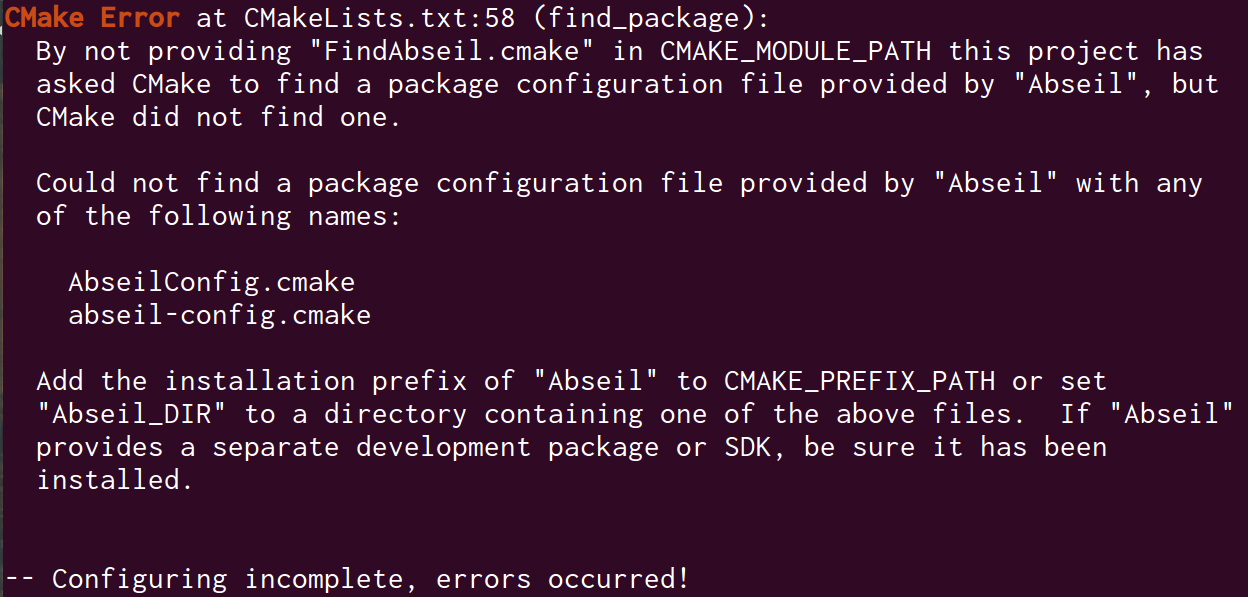

1
2
3
4
git clone https://github.com/abseil/abseil-cpp.git
cd abseil-cpp
cmake -L CMakeLists.txt && make
sudo make install

编译时会有个问题，需要加C++11，在absl文件夹里的CMakeList.txt里面添加set(CMAKE_CXX_FLAGS "-std=c++11") 或者 add_compile_options(-std=c++11)

如果还是缺少文件，就按照find_package的要求配置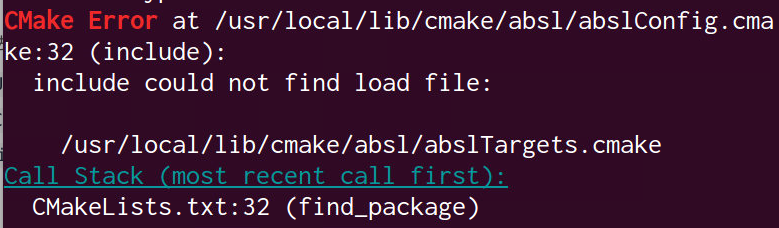
缺abslTargets.cmake.png

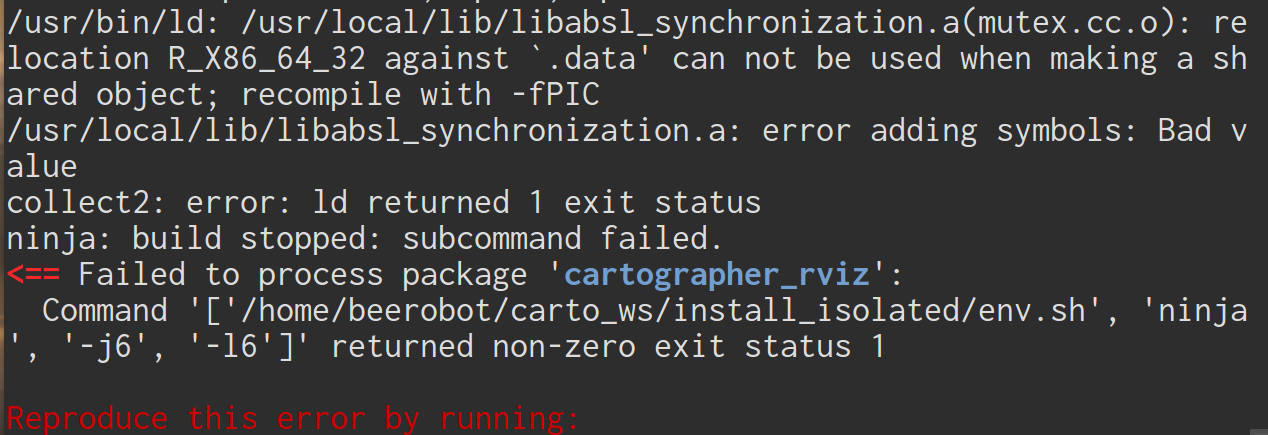
编译cartographer_rviz出错.png
这个问题困扰我好久，最后终于发现在编译absl库时的cmake没有加 -fPIC flag，所以执行 cmake -DCMAKE_POSITION_INDEPENDENT_CODE=ON ..，这样就永久解决这个问题了。

要注意报错信息，找的是AbseilConfig.cmake 或者 abseilConfig.cmake，查看cartographer_ros的CMakeLists。 我的abseil装完是在/usr/local/lib/cmake/absl/abslConfig.cmake

1
2
3
# 添加查找目录
set(Abseil_DIR "/usr/local/lib/cmake/absl")
find_package(Abseil REQUIRED)


后来我又用另一种方式解决了

从github下载 abseil-cpp-20190808.1，解压后执行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
git clone https://github.com/abseil/abseil-cpp.git
cd abseil-cpp
git checkout 215105818dfde3174fe799600bb0f3cae233d0bf # 20211102.0
mkdir build
cd build
cmake -G Ninja \
  -DCMAKE_BUILD_TYPE=Release \
  -DCMAKE_POSITION_INDEPENDENT_CODE=ON \
  -DCMAKE_INSTALL_PREFIX=/usr/local/stow/absl \
  ..
ninja
sudo ninja install
cd /usr/local/stow
sudo stow absl

修改cartographer_ros/CMakeLists.txt的部分：

1
2
set(absl_DIR "/usr/local/stow/absl/lib/cmake/absl")
find_package(absl REQUIRED)

Protobuf

安装cartogapher新版本时候，编译后遇到Unrecognized syntax identifier "proto3". This parser only recognizes "proto2"。

检查protobuf版本: protoc --version 显示的是2.6版本。
使用locate protoc发现我有两个protc，在/usr/bin和/usr/local/bin，分别检查版本，发现都是2.6。再次使用md5sum检查，发现两个文件完全一样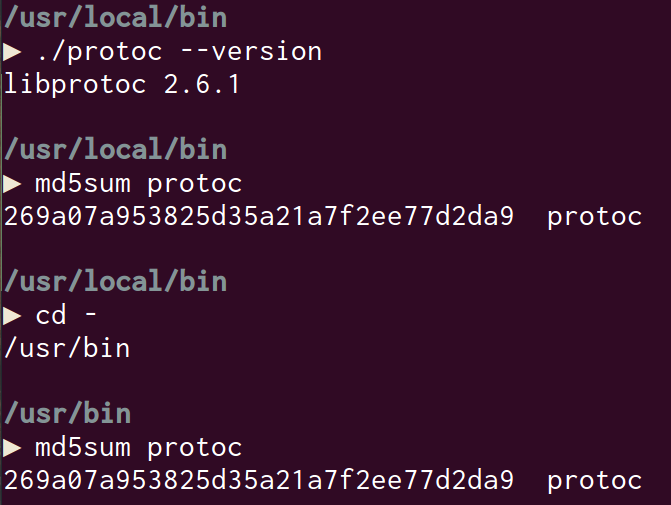
检查protoc.png

安装 Protobuf

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 版本不要太新
VERSION="v3.4.1"

# Build and install proto3.
git clone https://github.com/google/protobuf.git
cd protobuf
git checkout tags/${VERSION}
mkdir build
cd build
cmake -G Ninja \
  -DCMAKE_POSITION_INDEPENDENT_CODE=ON \
  -DCMAKE_BUILD_TYPE=Release \
  -Dprotobuf_BUILD_TESTS=OFF \
  ../cmake
ninja
sudo ninja install

或者

1
2
3
4
5
6
7
8
9
10
11
sudo apt-get install autoconf autogen
git clone https://github.com/protocolbuffers/protobuf.git
cd protobuf
git submodule update --init --recursive
./autogen.sh
./configure
make
# 这一步可能会报错，无视就好
make check
sudo make install
sudo ldconfig # refresh shared library cache.

检查一下安装后protobuf的版本，protoc --version

编译器优先找了/usr/bin/protoc的版本, 新安装的proto3是放在/usr/local/bin/protoc下的，可以删除/usr/bin/protoc，然后把/usr/local/bin/protoc放入/usr/bin，或者建立软连接：

1
2
sudo mv /usr/bin/protoc /usr/bin/protoc.bk
sudo ln -s /usr/local/bin/protoc /usr/bin/protoc

编译

有时编译遇到错误，只删除build_isolated/cartographer_ros/CMakeFiles即可，不用全删编译完成的文件