
matlab的操作步骤:
- 产生独立变量,为带有两个变量 x 和 y 的集合,meshgrid是一个可以建立独立变量的函数,产生矩阵元素,元素x和y按照指定的范围和增量来产生。
- 输入要使用的函数
- 调用contour(x,y,w)命令,contour函数是画一个多维函数的等高线
1 | [x,y] = meshgrid(-5:0.05:5,-5:0.05:5) |
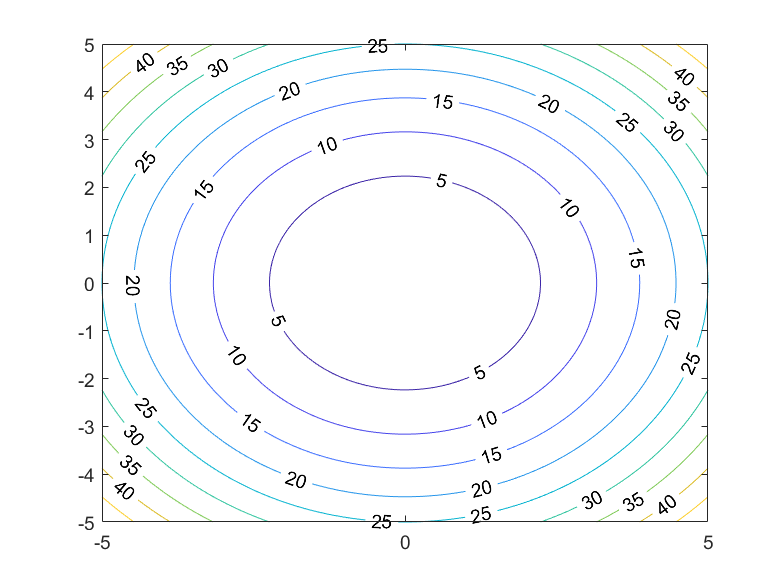
surf函数用于画三维的等高线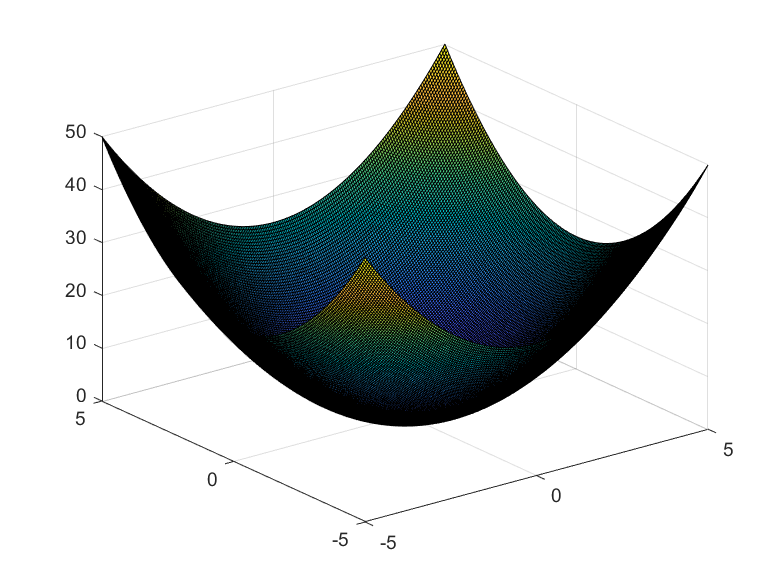
高维高斯分布的概率密度函数和等高线图
1 | u=[0;0];%均值 |
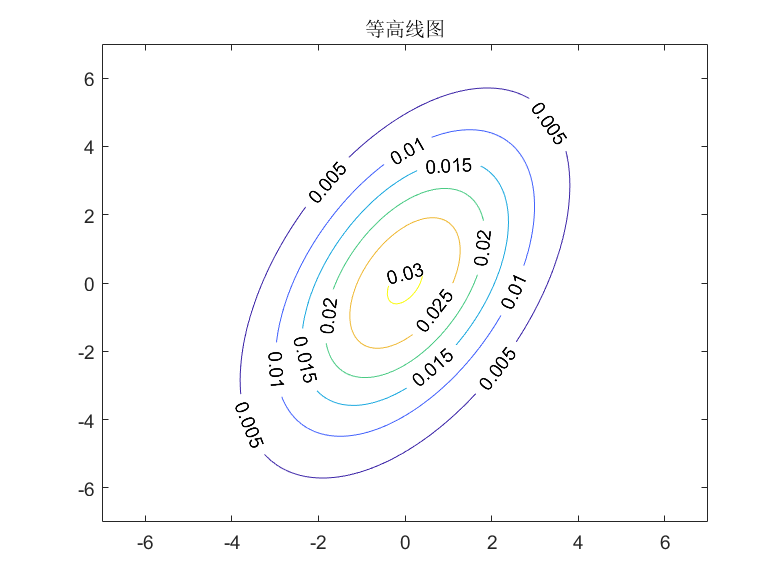
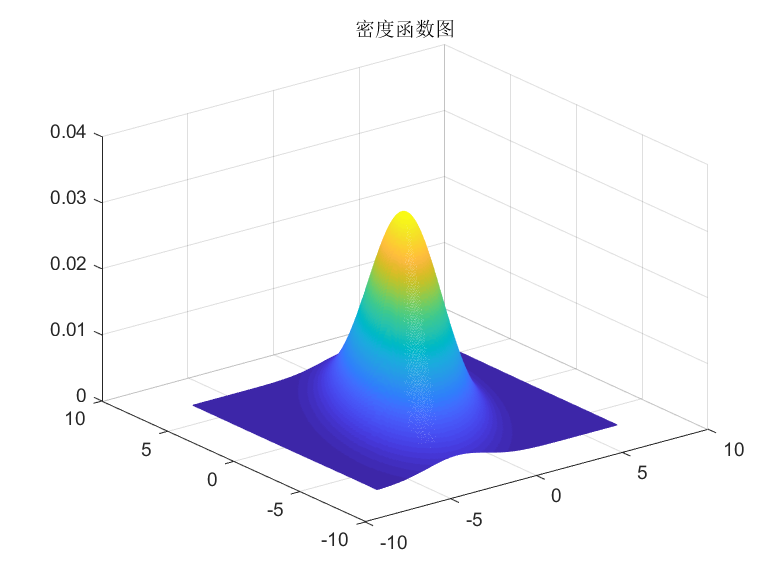

matlab的操作步骤:
1 | [x,y] = meshgrid(-5:0.05:5,-5:0.05:5) |

surf函数用于画三维的等高线
高维高斯分布的概率密度函数和等高线图
1 | u=[0;0];%均值 |


ceres-solver和g2o的性能对比,从优化精度和速度两方面来看,对于不同的数据集,各有优劣,难以比较。
ceres是google库,首先安装相关依赖1
2
3sudo apt-get install -y libatlas-base-dev
sudo apt-get install -y liblapack-dev libsuitesparse-dev libcxsparse3.1.2 libgflags-dev
sudo apt-get install -y libgoogle-glog-dev libgtest-dev
如果使用Ubuntu18.04,安装libcxsparse3.1.2可能出错,ubuntu从18.04版本开始,libcxsparse这个包的名称改为libcxsparse3。具体方法参考安装Ceres相关依赖时libcxsparse3.1.2报错
如果安装时找不到 cxsparse 或者其他的lib,需要添加下面的源1
sudo vim /etc/apt/sources.list
把下面的源粘贴到source.list的最上方: deb http://cz.archive.ubuntu.com/ubuntu trusty main universe
更新一下: sudo apt-get update, 然后再进行第一步的安装。
从github上下载,这里要注意ceres的版本和Eigen是搭配的,ceres版本越新,对Eigen的版本要求也越新,它的CMakeLists里有提示,所以不要安装最新的。 安装2.0.0 即可
下载解压后执行老一套命令:1
2
3
4
5mkdir build
cd build
cmake ..
make
sudo make install
安装官方的说明配置是错误的,应该是这样:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15find_package(Ceres REQUIRED)
INCLUDE_DIRECTORIES(/usr/include/eigen3)
include_directories(
${catkin_INCLUDE_DIRS}
# 这行可以没有
${CERES_INCLUDE_DIRS}
)
add_executable(program src/program.cpp)
target_link_libraries(program
${catkin_LIBRARIES}
${CERES_LIBRARIES}
)
如果这样报错,找不到ceres,就加上set(Ceres_DIR "/usr/local/lib/cmake/ceres"), 也可能是 /usr/local/lib/cmake/ceres
ceres使用LM或狗腿算法,求解参数的数据类型只支持 double*。Ceres相对于g2o的缺点仅仅是依赖的库多一些(g2o仅依赖Eigen).但是可以直接对数据进行操作
ceres是求解给定函数的最小值
Solver::Options::trust_region_strategy_type 可以取LEVENBERG_MARQUARDT或DOGLEG
Solver::Options::use_inner_iterations 设为True,可以启用 Ruhe & Wedin的非线性推广的算法II。这个版本的Ceres具有更高的迭代复杂度,但是每次迭代都显示更好的收敛行为。把 Solver::Options::num_threads设为最大值是非常值得推荐的
minimizer_progress_to_stdout
num_threads: 设置使用的线程,但有时线程少反而用时更少,不明白为什么
对于非线性最小二乘问题,最终转化为求解方程
Ceres提供了很多计算的方法,这就涉及Solver::Options::linear_solver_type的取值问题
默认值。 适合使用稠密雅可比矩阵的小规模问题(几百个参数和几千个残差),也就是使用Eigen库的稠密矩阵QR分解。如果ceres优化问题不是SLAM的大型后端,不是稀疏问题,使用DENSE_QR
大规模的非线性最小二乘问题通常是稀疏的。对于这种情况使用稠密QR分解是低效率的,改用Cholesky因式分解,它有两种变体 - 稀疏和密集。
DENSE_NORMAL_CHOLESKY是执行正规方程的稠密Cholesky分解。 Ceres使用Eigen稠密的LDLT因式分解算法。
SPARSE_NORMAL_CHOLESKY是执行正规方程的稀疏Cholesky分解,这为大量稀疏问题节省了大量的时间和内存消耗。Ceres使用SuiteSparse 或 CXSparse库中的稀疏Cholesky分解算法 或 Eigen中的稀疏Cholesky分解算法。
如果Ceres编译时支持了这三个库,那么linear_solver_type默认值是SPARSE_NORMAL_CHOLESKY,否则就是DENSE_QR。使用最多的是DENSE_QR,cartographer前端的ceres scan mather用的也是DENSE_QR
CGNR : 使用共轭梯度法求解稀疏方程
DENSE_SCHUR & SPARSE_SCHUR : 适用于BA问题
ceres::Solver::Summary summary;
直接使用summary.total_time_in_seconds
int Solver::Summary::num_threads_given: Number of threads specified by the user for Jacobian and residual evaluation.
int Solver::Summary::num_threads_used
Number of threads actually used by the solver for Jacobian and residual evaluation. This number is not equal to Solver::Summary::num_threads_given if none of OpenMP or CXX_THREADS is available.
以上两个线程的参数是由Options::num_threads决定的,如果设置太大,这两个参数就会不同,只会用最大线程数。
min_linear_solver_iteration 和 max_linear_solver_iteration:线性求解器的最小/最大迭代次数,默认为0/500,一般不需要更改
max_num_iterations : 默认是50。求解器的最大迭代次数,并不是越大越好。对于SLAM前端的实时性有要求,所以max_num_iterations不能太大,ALOAM里设置为4
bool Solver::Summary::IsSolutionUsable() const
算法返回的结果是否数值可靠。 也就是Solver::Summary:termination_type是否是CONVERGENCE, USER_SUCCESS 或者 NO_CONVERGENCE,也就是说求解器满足以下条件之一:
通过实验发现除了多线程以及 linear_solver_type,别的对优化性能和结果影响不是很大
例子1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.259266e+05 0.00e+00 5.00e+04 0.00e+00 0.00e+00 1.00e+04 0 1.91e-05 1.26e-04
1 2.468045e+04 1.01e+05 2.69e+02 1.31e+01 1.00e+00 3.00e+04 1 5.60e-05 2.02e-04
2 2.467825e+04 2.20e+00 1.17e+00 5.00e-02 1.00e+00 9.00e+04 1 2.29e-05 2.37e-04
Solver Summary (v 2.0.0-eigen-(3.3.4)-lapack-suitesparse-(5.1.2)-cxsparse-(3.1.9)-eigensparse-no_openmp)
Original Reduced
Parameter blocks 4 3
Parameters 12 9
Residual blocks 5 5
Residuals 15 15
Minimizer TRUST_REGION
Sparse linear algebra library SUITE_SPARSE
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver SPARSE_NORMAL_CHOLESKY SPARSE_NORMAL_CHOLESKY
Threads 1 1
Linear solver ordering AUTOMATIC 3
Cost:
Initial 1.259266e+05
Final 2.467825e+04
Change 1.012484e+05
Minimizer iterations 3
Successful steps 3
Unsuccessful steps 0
Time (in seconds):
Preprocessor 0.000106
Residual only evaluation 0.000009 (3)
Jacobian & residual evaluation 0.000026 (3)
Linear solver 0.000053 (3)
Minimizer 0.000166
Postprocessor 0.000004
Total 0.000276
Termination: CONVERGENCE (Function tolerance reached. |cost_change|/cost: 6.530805e-10 <= 1.000000e-06)
Initial Cost 从 1.259266e+05 变为 Final Cost的 2.467825e+04,变化不够大。 如果 Initial cost 和 Final Cost 差别很小,说明优化之前的数据已经足够好
参考:
官方教程学习笔记(十三)
欧氏变换(Isometry Transform)可以看作是维持任意两点距离不变的变换,在实际场景中使用比较多。在Eigen中已经内置好了一些常用的欧氏变换:1
2
3
4typedef Transform<float,2,Isometry> Isometry2f;
typedef Transform<float,3,Isometry> Isometry3f;
typedef Transform<double,2,Isometry> Isometry2d;
typedef Transform<double,3,Isometry> Isometry3d;
欧氏变换必须初始化,如果没初始化,Isometry3d中的元素全为0,一般初始化为单位矩阵,也可以初始化为Quaternion。 赋值可以通过它的成员函数.rotate()和.translate()完成
1 | AngleAxisd rotation(3.1415926 / 4, Vector3d(1, 0, 1).normalized()); |
A.translate(B)等价于A×B,而A.pretranslate(B)等价于B×A,对应于左乘和右乘的区别。凡是前面带pre的函数,其变化都是相对于上一步变化之前的状态进行的。举例说我要新建一个按固定轴先平移后旋转的变换。但我首先设置了旋转,然后再设置平移。这个时候设置平移就不能用translate()了,而应该用pretranslate()。因为第一步已经对坐标系进行了旋转,后面的平移是在旋转后的坐标系中进行的,所以最好不要用pre开头的函数
针对求解Ax = b这种线性问题,Eigen提供了下面几种分解方法,每一种方法都提供了一个solve()函数以便求解得到 x,Eigen对每一种分解方法的速度和精度做了如下对比。当然对于小矩阵,各个方法没什么区别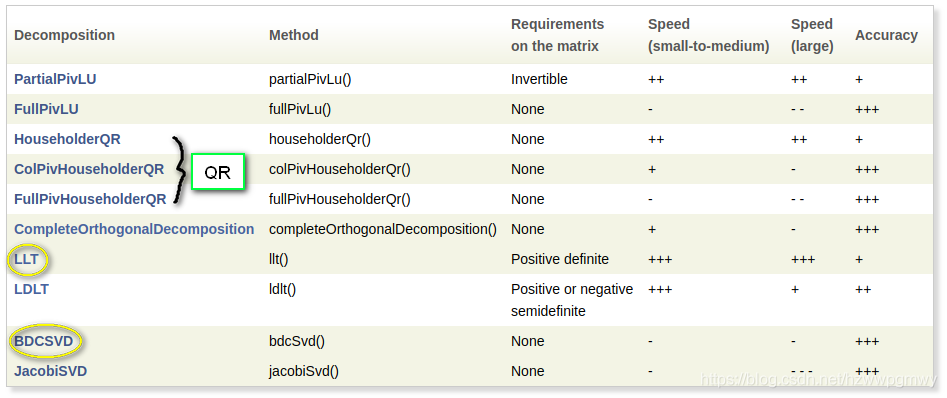
LLT(cholesky)是最快的求解器,但是精度也是最差的,并且只能对正定矩阵进行分解,而LDLT则可以应对正半定和负半定问题,精度较LLT更高,所以尽量使用LDLT,但是LDLT在求解大矩阵问题时,耗时较QR增加更多,所以究竟选择那种分解方式求解问题,需要根据速度和精度综合考量
使用info()判断是否收敛1
2
3SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
if (eigensolver.info() != Success)
abort();
对于自伴随矩阵,Eigen使用SelfAdjointEigenSolver进行特征值分解1
2
3
4Eigen::SelfAdjointEigenSolver< Eigen::Matrix3d > eigen_solver( matrix_33 );
// 特征值 特征向量
cout << "Eigen values = " << eigen_solver.eigenvalues( ) << endl;
cout << "Eigen vectors = " << eigen_solver.eigenvectors( ) << endl;
Cholesky分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。Eigen的LLT分解实现了Cholesky分解。代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int main(int argc, char** argv)
{
Eigen::Matrix2d down;
down<<1,0,
2,1;
// A <<1,2
// 2,5
Eigen::Matrix2d A = down*down.transpose();
std::cout<<"A: "<< A <<std::endl;
// 直接用 llt() 函数
Eigen::Matrix2d ml = A.llt().matrixL();
Eigen::Matrix2d testA = ml*ml.transpose();
std::cout<<"mllt: "<< ml<<std::endl;
std::cout<<"testA: "<<testA<<std::endl;
return 0;
}
对于Ax=b,LLT分解并不会检查 A 矩阵的对称性,所以如果你输入的 A 矩阵不是正定的Hermite矩阵,你也会得到分解结果,只不过是错误的
LDLT分解法实际上是Cholesky分解法的改进,优先使用LDLT而不是LLT方法。 Cholesky分解法虽然不需要选主元,但其运算过程中涉及到开方问题,而LDLT分解法则避免了这一问题。仍然要求A矩阵正定。 其中L为下三角形 单位 矩阵(即主对角线元素皆为1,下三角其他元素不为0),D为对角矩阵, 为L的转置矩阵。1
2
3
4
5
6
7Matrix2f A, b;
A << 2, -1, -1, 3;
b << 1, 2, 3, 1;
cout << "Here is the matrix A:\n" << A << endl;
cout << "Here is the right hand side b:\n" << b << endl;
Matrix2f x = A.ldlt().solve(b);
cout << "The solution is: \n" << x << endl;
1 | Matrix3f A; |
特征值分解仅针对方阵,而不是方阵的矩阵就有了SVD分解:
其中A为m x n的矩阵, 正交矩阵 U(m x m阶) 和 V(n x n阶)。
矩阵U的列称为左奇异向量, 是正交的。矩阵V的列向量(也称为右奇异向量)也是正交的.
此时的A如果是方阵,那么逆矩阵也很容易求出:
奇异值分解同时包含了旋转、缩放()和投影三种作用。特征值分解只有缩放的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27Eigen::Matrix3f A;
A << 3,4,2,
1,2,4,
8,0,1;
// SVD分解
Eigen::JacobiSVD<Eigen::Matrix3f> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);
// 求出三个矩阵
Eigen::Matrix3f U = svd.matrixU();
Eigen::Matrix3f V = svd.matrixV();
// 推荐方法,从对角线元素组成的向量直接构造对角矩阵
Eigen::Matrix3f diag = svd.singularValues().asDiagonal();
cout << "U: "<<endl<< U <<endl<<endl;
cout << "V transpose: "<< endl << V.transpose() <<endl<<endl;
cout << "Sigma from SVD: "<< endl << diag<<endl<<endl;
// 判断U和V是否正交矩阵(酉矩阵),和转置的乘积为单位矩阵
cout << U.isUnitary() <<endl<<endl;
cout << V.isUnitary() <<endl<<endl;
cout <<"***********************"<<endl;
// 从公式推导出的对角矩阵,有误差
Eigen::Matrix3f Sigma = U.inverse() * A * V.transpose().inverse();
cout << "Sigma from formula: "<< endl << Sigma <<endl<<endl;
// 大致等于原矩阵A
cout<< "A from formula: "<< endl <<U *Sigma *V.transpose()<<endl;
运行结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
U:
0.4853 -0.514629 -0.706853
0.299358 -0.661777 0.68734
0.821504 0.545168 0.167102
V transpose:
0.904647 0.275928 0.324773
0.423663 -0.664689 -0.615385
-0.0460712 -0.6943 0.71821
S from SVD:
9.20501 0 0
0 5.0882 0
0 0 2.09237
1
1
***********************
S from formula:
9.20501 -9.53674e-07 -2.38419e-07
-1.3113e-06 5.0882 1.05798e-06
-7.15256e-07 2.90573e-07 2.09237
A from formula:
3 4 2
1 2 4
8 0 1
Eigen提供了两个类以实现SVD分解:BDCSVD(大矩阵)和JacobiSVD(小矩阵),推荐使用BDCSVD,因为当发现要分解的矩阵是小矩阵时,将自动切换到JacobiSVD
把上面的ComputeFullU换成ComputeThinU,那么 就是一个正交矩阵B1
2
3
4
5
6
7
8
9// SVD分解, ComputeThin参数时,A必须是 Eigen::MatrixXf
Eigen::JacobiSVD<Eigen::MatrixXf> svd(A, Eigen::ComputeThinU | Eigen::ComputeThinV );
// 求出三个矩阵,这样B就是个正交矩阵
Eigen::Matrix3f U = svd.matrixU();
Eigen::Matrix3f V = svd.matrixV();
Eigen::Matrix3f B = U * V.transpose();
cout << B.transpose() << endl <<endl;
cout << B.inverse() << endl<<endl;
如果一个线性方程组是超定的(overdeterminated,未知数个数>方程数),这时候常规方法无解,就需要用最小二乘拟合最优结果。最精确的解法是SVD分解。SVD也有多种解法,官方推荐的是BDCSVD方法。
如下超定方程组: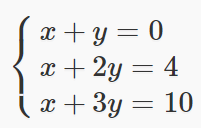
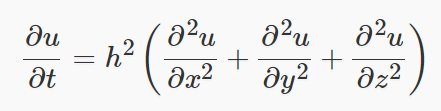
最小二乘求解代码如下:1
2
3
4
5
6
7
8
9
10MatrixXf A(3, 2);
Vector3f b;
Vector2f x;
A << 1,1, 1,2, 1,3 ;
b << 0,4,10;
x = A.bdcSvd(ComputeThinU | ComputeThinV).solve(b);
cout << x << endl;
Vector3f error = (A*x - b).cwiseAbs();
double mean_error = error.mean();
程序运行需要一点时间,最后得到的x就是通过最小二乘算出来的。这里bcdScd()函数里面的参数ComputeThinU | ComputeThinV必须要写(可以先记住),否则会报错。
将得到的解带回方程会发现其并不是严格成立的,有时可能还会相差较大。这是因为对于超定方程,采用最小二乘法得出的解并不一定对每一个方程都严格成立,其确保的是当前解在所有方程上的总误差最小。得到解以后我们可以反算出其解的整体精度
对于小矩阵,逆矩阵和行列式随便算,如果是大矩阵,计算量会很庞大。确定你是否真的需要逆矩阵,因为很多时候求逆矩阵都是为了求解Ax = b问题,所以最好使用上面介绍的分解方法代替.
参考:
Eigen学习与使用笔记
Eigen学习与使用笔记2
Eigen官方文档-AngleAxis
矩阵的特征分解与奇异值分解
shared_ptr 内部包含两个指针,一个指向对象,另一个指向控制块,控制块中包含一个引用计数和其它一些数据。由于这个控制块需要在多个shared_ptr之间共享,即多个shared_ptr可以共享同一块内存,所以它也是存在于 heap 中的。
如果没有共享所有权的必要,就不必使用shared_ptr,而非unique_ptr
由于支持共享所有权,shared_ptr支持拷贝和赋值运算, 也支持移动。如果对象在创建的时候没有使用共享指针存储的话,之后也不能用共享指针管理这个对象了。
避免使用原生指针来创建shared_ptr指针
shared_ptr销毁对象的情况:
shared_ptr给一个shared_ptr初始化shared_ptr的缺点:
内存占用是原生指针的两倍,因为除了要管理一个原生指针外,还要维护一个引用计数
使用了性能低的原子操作:考虑到线程安全问题,引用计数的增减必须是原子操作。 而原子操作一般情况下都比非原子操作慢
两个shared_ptr可能出现循环引用,永远不能释放指向的对象
shared_ptr有两个成员,指向对象的指针ptr和管理引用计数的指针ref_count。引用计数本身是原子操作,是线程安全的,但 shared_ptr的赋值操作由复制对象指针和修改使用计数两个操作复合而成, 因此仍不是线程安全的。如果要从多个线程读写同一个shared_ptr 对象,还是需要加锁。
陈硕专门写了这篇文章分析这个问题,
也可以看我自己的这篇文章,子线程里能写shared_ptr指向的对象,回到主线程就变了。
为了节省一次内存分配,原来shared_ptr<Foo> x(new Foo); 需要为 Foo 和 ref_count 各分配一次内存,现在用make_shared()的话,可以一次分配一块足够大的内存,供 Foo 和 ref_count 对象容身。
1 | int num = 12; |
p1的用法是错的,p2和p3正确,但是不要同时使用,改用p3(p2)即可
1 | boost::shared_ptr<Foo> a; |
执行a->out()会报错,原因是a没有指向对象,应该这样定义:boost::shared_ptr<Foo> a(new Foo());
再看这样的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14boost::shared_ptr<Foo> a(new Foo()); // 让a指向对象
cout<< a.use_count()<<endl; // 1
boost::shared_ptr<Foo> b = a; // 另一个指针也指向同一个对象
cout<< a.use_count()<<endl; // 2
cout<< b.use_count()<<endl; // 2
a.reset(); // 不执行析构函数,实际执行 delete a; a = NULL;
a->out(); // 报错
b->out(); // 正常
cout<< a.use_count()<<endl; // 0
cout<< b.use_count()<<endl; // 1
b.reset(); // 执行析构函数
cout<<"end"<<endl;
只有对象的引用计数为0的时候,才执行类的析构和free其内存:1
2
3
4
5
6
7
8
9boost::shared_ptr<Foo> a(new Foo());
boost::shared_ptr<Foo> b = a;
cout<<a<<endl;
cout<<b<<endl;
a.reset(new Foo()); // a重新初始化,指向另一个地址
cout<<a<<endl;
cout<<b<<endl;
运行结果:1
2
3
4
50x99fc20
0x99fc20
0x9a0c70
0x99fc20
不要把一个原生指针给多个shared_ptr管理1
2
3int* ptr = new int;
boost::shared_ptr<int> p1(ptr);
boost::shared_ptr<int> p2(ptr);
这样做会导致ptr会被释放两次。在实际应用中,保证除了第一个shared_ptr使用ptr定义之外,后面的都采用p1来操作,就不会出现此类问题。
可以在标准容器里存储boost::shared_ptr,但不能存储std::auto_ptr和boost::scoped_ptr,后两者不能共享对象所有权.1
2
3std::vector<boost::shared_ptr<int> > v;
v.push_back(boost::shared_ptr<int>(new int(1)));
v.push_back(boost::shared_ptr<int>(new int(2)));
默认情况下,shared_ptr调用delete()函数进行资源释放,即delete p;。但是如果shared_ptr指向一个数组而不是一个简单的指针,应该调用delete[] p,此时可以将一个回调传递给shared_ptr的构造函数来定制删除器。
主要是利用了构造函数template<class Y, class D> shared_ptr(Y * p, D d);,第一个参数是要被管理的指针, 与其它形式的构造函数一致; 第二个参数称为删除器, 他是一个接受Y*的可调用物, d(p)的行为应类似与delete p, 而且不应该抛出异常。有了删除器, 我们就可以管理一些更复杂的资源, 比如数据库连接, socket连接。
其实有很多种用法,只列举常用的普通函数法1
2
3
4
5
6
7
8
9Derived *d = new Derived[5];
boost::shared_ptr<Derived> p1(d, deleter);
// deleter函数定义
void deleter(Derived* d)
{
delete[] d;
cout<<"delete"<<endl;
}
因为要求在Windows上间接运行ROS的程序, 采用的通信方式是Web API. Web API可以使用任何类型的通信协议,数据交互格式为XML以及JSON。但主要是JSON,因为它比XML更加轻量,这就是使得JSON在解析速率方面更快,对带宽的要求更低。实际使用的还是Http的GET方式,所以把ROS程序做成CGI的形式, 放到mini-httpd的网络目录里供windows调用
Web API的客户端系统(调用者)和服务系统(提供者)彼此独立,调用者可以轻易的使用不同的语言(Java,Python,Ruby等)进行API的调用。
Web API的测试工具是POSTMAN, 在Windows和Linux平台下均有
这里要多说一些内容, 机器人上用到的Web API通信比较多,如果自己在文档上总结,不太方便且容易出错,看到仙知机器人使用Swagger总结的很好: RoboRoute Web API 使用手册
Swagger是一款RESTFUL接口的文档在线自动生成+功能测试功能软件,随着现在许多公司实现了前后端分离,swagger越来越受欢迎了。swagger是有两个版本的,而且区别还挺大的,一个是swagger-ui也就是swagger1;还有一个是springfox-swagger也就是swagger2. 推荐用前者.
Swagger UI 提供了一个可视化的UI页面展示描述文件。接口的调用方、测试、项目经理等都可以在该页面中对相关接口进行查阅和做一些简单的接口请求。该项目支持在线导入描述文件和本地部署UI项目。
查看Boost版本: grep BOOST_LIB_VERSION /usr/include/boost/version.hpp 或者 dpkg -s libboost-dev | grep 'Version'
Boost中有一个noncopyable类,它把copy构造函数和赋值运算符都声明为private,可以让自定义的类继承它
1 | class noncopyable |
上面拷贝构造函数和赋值构造函数都声明为private,这样不论什么派生方式,子类对此都是无权访问的,从而达到禁止拷贝的目的。
构造函数为什么声明成protected呢? 首先肯定不能为private,不然无法构造子类实例。
如果为public,那么外部是可以创建noncopyable这么一个实例的,可是这个实例是完全没有意义的,我们用不到,该类只有在被继承之后才有意义。
所以此处声明为protected才是合适的,既保证外部无法直接构造一个无意义的noncopyable实例,又不影响构造子类实例。
但是如果派生类继承它之后,又定义自己的copy构造和赋值运算符,调用者还是能够通过赋值和copy构造等手段来产生一个新的对象,这种情况干脆不要继承noncopyable类
大端: 低位的数据存放在高地址,高位的数据存放在低地址
小端: 低位的数据存放在低地址,高位的数据存放在高地址
现在的CPU一般都是小端. 网络编程中,TCP/IP统一采用大端方式传送数据,所以有时我们也会把大端方式称之为网络字节序
结合union理解这个概念比较容易,看下面程序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18union my{
int a;
char bytes[4];
};
my un;
un.a = 135201034;
// a为4个字节, 二进制表示就是: 00001000 00001111 00000001 00001010
// 分别转化为十进制就是 8 15 1 10
int a0 = static_cast<int>(un.bytes[0]) ;
int a1 = static_cast<int>(un.bytes[1]) ;
int a2 = static_cast<int>(un.bytes[2]) ;
int a3 = static_cast<int>(un.bytes[3]) ;
cout<< "address a0: "<< &a0 <<" "<<a0 <<endl;
cout<< "address a1: "<< &a1 <<" "<<a1 <<endl;
cout<< "address a2: "<< &a2 <<" "<<a2 <<endl;
cout<< "address a3: "<< &a3 <<" "<<a3 <<endl;
联合体占了4个字节,对a赋值后,显然bytes数组要分担这4个字节的数据,这里为了表示清楚,把每个bytes又转为int(四个字节),我们知道数组的内存地址占用是连续的,而且第一个元素在低地址,依次为高地址。
运行结果:1
2
3
4address a0: 0x7fff768cc180 10
address a1: 0x7fff768cc184 1
address a2: 0x7fff768cc188 15
address a3: 0x7fff768cc18c 8
可以看出转换后,每个占了4字节,低地址的a0对应的是a的低8位,所以说这里是小端. 如果是大端, 地址和数据的对应关系就要倒过来.
智能指针三个优点:
智能指针类重载了解引用运算符(*)和成员指向运算符(->),同时为了能够在堆中管理各种类型,几乎所有的智能指针都是模板类,包含其功能的泛型实现。
C++11 中的auto_ptr已经废弃. 现有的 unique_ptr,shared_ptr,weak_ptr和原生指针加起来构成了指针的完整四件套。它们都在头文件<memory>里面,最常用的是原生指针(没所有权语义的时候),其次是unique_ptr,后两个除非特定场合需求,能不用就不用。 拷贝shared_ptr、 weak_ptr都涉及到atomic操作,其开销比起拷贝、解引用一个指针都是大很多的。
unique_ptr代表的是专属所有权,之所以叫这个名字,是因为它只能指向一个对象,即当它指向其他对象时,之前所指向的对象会被摧毁,不能进行复制操作只能进行移动操作。两个unique_ptr也不能指向一个对象. 看源码发现,拷贝构造函数和赋值运算符都加了delete:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16template <typename T, typename D = default_delete<T> >
class unique_ptr
{
public:
explicit unique_ptr(pointer p) noexcept;
~unique_ptr() noexcept;
T& operator*() const;
T* operator->() const noexcept;
unique_ptr(const unique_ptr &) = delete;
unique_ptr& operator=(const unique_ptr &) = delete;
unique_ptr(unique_ptr &&) noexcept;
unique_ptr& operator=(unique_ptr &&) noexcept;
// 省略 ...
private:
pointer __ptr;
};
强行使用会报错: 
这里需要注意: 既然不能拷贝, 就不能在函数中将unique_ptr作为参数了,因为传参是一个产生副本的过程,用 move(unique_ptr)取代
unique_ptr析构时,它的析构函数将会负责析构它持有的对象,还可以使用自定义的 删除器operator*() 和 operator->()成员函数,像 raw pointer 一样,我们可以使用*解引用unique_ptr,使用->来访问unique_ptr所持有对象的成员。unique_ptr并不提供 copy 操作,但提供了 move 操作,因此可以用std::move()来转移unique_ptr, 把一个unique_ptr的内存交给另外一个unique_ptr对象管理,。转移之后,当前对象不再持有此内存,新的对象将获得专属所有权std::make_unique<T>()函数用来直接创建unique_ptr,但 C++11 没有unique_ptr和原生指针的大小是一样的,内存上没有任何的额外消耗,性能是最优的
如果没有为unique_ptr指定对象,get()返回0
1 | class Test |
move不执行析构,否则新的智能指针无法指向对象了.
reset有两种用法
如果不加参数,就会销毁对象(执行析构函数),重置智能指针
如果加原生指针做参数,就会先销毁原来指向的对象,然后指向原生指针指向的对象
1 | Test* p3 = new Test(); |
运行结果:1
2
3
4
5
6
7
8construct // p3
construct // p4
p4: 0x7adc50
destruct //
after reset
p4: 0x7acc20
p3: 0x7acc20
destruct
需要注意: release不执行析构, reset执行析构
unique_ptr的定义删除器方式和shared_ptr不同,因为模板的参数不同,前者还需要指定删除器类型.
原型有:
T为指针管理的对象类型, D为删除器类型, t为管理的对象, d为删除器函数名称
1 | void myclose(Test* t) |
运行结果:1
2
3construct
close func
destructdecltype用于获取myclose的类型, *表面它是一个指针类型,即函数指针.
make_unique 不是‘std’的成员 , 原因是make_unique为C++14才特有的, 如果使用gcc版本小于6.2,编译就会报错,vs2015 msvc 也可以
单链表程序如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27struct LinkedList
{
int data;
LinkedList* next;
};
LinkedList* root, *second, *third;
root = new LinkedList;
second = new LinkedList;
third = new LinkedList;
root->data = 10;
root->next = second;
second->data = 20;
second->next = third;
third->data = 30;
third->next = nullptr;
LinkedList* guy = new LinkedList;
guy->data = 90;
guy->next = second->next;
second->next = guy;
while(root)
{
cout<< root->data <<endl;
root = root->next;
}
deque可以看做是vector和list的折中容器,类似vector,它支持随机访问(其实是假象),即支持[]以及at(),但是性能没有vector好。
deque和vector的区别:
reserve, capacity函数。因为它是动态的以分段连续空间组合而成,随时可以增加一段新的空间并链接起来,不像 vector 那样,当旧空间不足而重新配置一块更大空间,然后复制元素,再释放旧空间deque还是不如list的任何位置插入删除,它的中间部分插入和删除元素和vector一样,时间复杂度还是O(n)。所以没有list的reverse函数
这下问题就来了,既然没有reserve和capacity,显然它和vector的底层机制不同。
deque采用类似索引的结构管理内存,采用一块所谓的map(不是数据结构的map )作为中控器,map是一块连续的内存空间,每个元素(称之为节点)都是指针,指向另一块连续的线性空间,称为缓冲区,map实际上是指针的指针T**。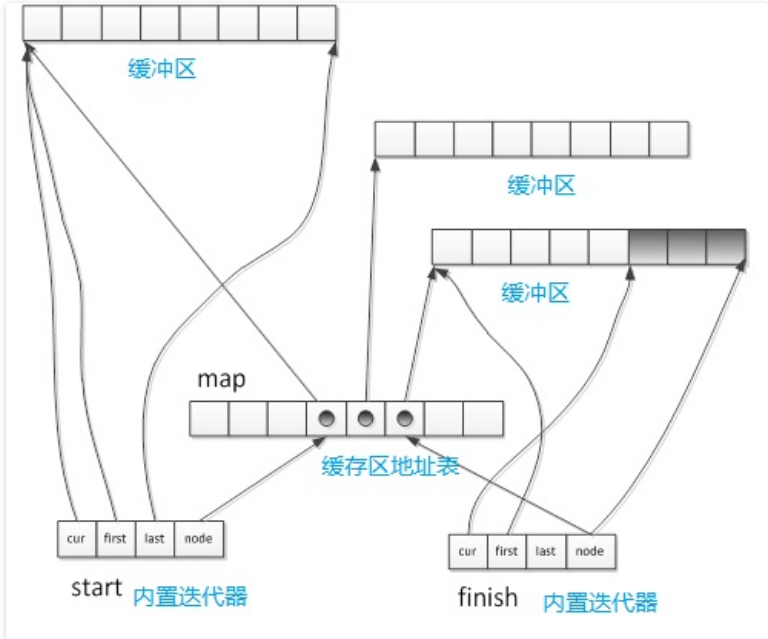
deque的迭代器包含4个:
cur:迭代器当前所指元素
first:此迭代器所指的缓冲区的头
last:缓冲区尾
node:指向管控中心
deque的最初状态是有一个缓冲区,调用clear函数的作用就会清除整个deque,释放所有空间而只保留一个缓冲区。如果调用erase清楚某个元素,而这个元素是所在缓冲区唯一的元素,会将此缓冲区释放。
与vector不同,deque的内存大小是可缩减的。deque的内存区块不再被使用时,会被释放。
deque维护start和finish两个迭代器,分别指向第一缓冲区的第一个元素和最后一个缓冲区的最后元素的下一个位置。它还要记住当前map的大小,如果map的节点不足,就需要重新配置。
为了指定缓冲区的大小,必须指定 alloc 为空间配置器。比如指定数据int类型,缓冲区大小为4的deque: deque<int, alloc, 4>。 map的初始大小至少是8,最多是所需节点数+2,按刚才的例子,要存放50个元素,就需要13个节点,那么map的初始大小就是15。 如果插入的元素太多,map会不够大,需要扩充,和vector的内存扩充一样,先配置一块更大的,把原来的节点全拷贝过来,再释放原来的map。 对于平时的空间扩充,如果缓冲区中还有备用的空间,那么直接使用备用的空间;否则另外配置一个缓冲区,将其信息记录到缓冲区地址表里
在除了首尾两端的其他地方插入和删除元素,都将会导致指向deque元素的任何pointers、references、iterators失效。
deque的元素存取和迭代器操作会比vector稍微慢一些,因为它的内部结构会多一个间接过程
deque迭代器是特殊的指针,而不是vector那样的一般指针,它需要在不同的区块之间跳转
不支持对内存分配时机的控制,也就是没有reserve
缓冲区的内存地址是连续的,但不同缓冲区之间不是连续的
中间添加元素,会使迭代器、指针、引用失效
头尾添加元素,现有元素的内存地址不变,指针和引用不失效,但迭代器可能失效,因为可能分配新的内存块
需要在两端插入和删除元素
随机访问元素的情况较少,主要是访问两端元素
要求容器释放不再使用的元素
cartographer中的成员变量,凡是以queue结尾的,基本都是deque类型。 比如timed_pose_queue,它的使用只有back, front, pop_back, pop_front几个函数,根本没有用到遍历和随机访问
1 | deque<std::unique_ptr<Constraint>> constraints_; |
constraints_是个vector,可先添加一个空元素,然后再对最后一个元素进行赋值,其实为添加一个新元素(cartographer中很多都是如此做法,目的可减省一个变量空间和赋值时间)
单向队列中的数据是先进先出,queue只是进一步封装别的数据结构,并提供自己的接口,如果不指定容器,默认是用deque来作为其底层数据结构的
单向队列一共6个常用函数front()、back()、push()、pop()、empty()、size(),不支持随机访问,所以没有[]运算符和at1
2
3
4
5
6
7
8
9
10
11
12
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
qDebug()<< q.size() << " "<< q.empty();
qDebug() <<q.front() << " " << q.back() ;
q.pop();
qDebug() <<q.front() << " " << q.back() ;
1 | 4 false |