1 | struct InsertionResult |
保存插入Local Slam的一个节点的数据结构,也就是下面这个东西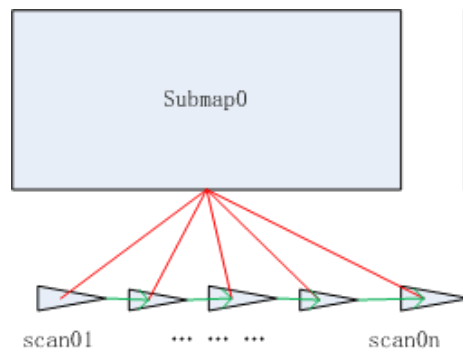
在类LocalTrajectoryBuilder2D中,通过对象active_submaps_来维护子图,它是一个ActiveSubmaps2D类型的数据。根据最新版本的代码,
除了刚开始构建的时候,没有子图(Submap2D),其他时候它都维护着两个子图对象。 一个子图用于进行扫描匹配,称为旧图。另一个子图用于插入扫描数据,作为储备,被称为新图。 当新图中插入一定数量的数据完成了初始化操作之后,它就会被当作旧图,用于扫描匹配。 对象active_submaps_将抛弃原来的旧图,并重新构建一个新图。下表中列出了所有成员变量
ActiveSubmaps2D的构造函数:1
2
3
4
5// std::unique_ptr<RangeDataInserterInterface> range_data_inserter_;
// 构建了插入器对象,代码只是根据配置对 ProbabilityGridRangeDataInserter2D 类的赋值
ActiveSubmaps2D::ActiveSubmaps2D(const proto::SubmapsOptions2D& options)
: options_(options), range_data_inserter_(CreateRangeDataInserter() )
{}RangeDataInserterInterface明显是个抽象类,它的派生类就是TSDFRangeDataInserter2D和ProbabilityGridRangeDataInserter2D,根据配置,我们一般用后者。 CreateRangeDataInserter()其实就是1
2
3return absl::make_unique<ProbabilityGridRangeDataInserter2D>(
options_.range_data_inserter_options()
.probability_grid_range_data_inserter_options_2d());
从InsertIntoSubmap函数开始,就是向子图插入传感器数据的过程,总流程:
InsertIntoSubmap
1 | struct RangeData { |
1 | /*InsertIntoSubmap( |
MotionFilter
motion_filter部分的IsSimilar是这个类唯一值得关注的函数,内容很简单1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21bool MotionFilter::IsSimilar(const common::Time time,
const transform::Rigid3d& pose)
{
LOG_IF_EVERY_N(INFO, num_total_ >= 500, 500)
<< "Motion filter reduced the number of nodes to "
<< 100. * num_different_ / num_total_ << "%.";
++num_total_;
if (num_total_ > 1 &&
time - last_time_ <= common::FromSeconds(options_.max_time_seconds()) &&
(pose.translation() - last_pose_.translation()).norm() <=
options_.max_distance_meters() &&
transform::GetAngle(pose.inverse() * last_pose_) <=
options_.max_angle_radians() )
{
return true;
}
last_time_ = time;
last_pose_ = pose;
++num_different_;
return false;
}
判断位姿和上一次插入scan的位姿是否超过一定的范围,然后再决定是否插入scan。 这个位姿就是ceres返回的位姿做重力对齐
ActiveSubmaps2D::InsertRangeData
这里是 插入子图的核心函数,有子图插入点云数据和终结子图两条线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19std::vector<std::shared_ptr<const Submap2D> >
ActiveSubmaps2D::InsertRangeData(const sensor::RangeData& range_data)
{
// vector<std::shared_ptr<Submap2D> > submaps_;
// 如果当前一个子图也没有,或最后一个子图的num_range_data达到配置值(抛弃旧图)
if (submaps_.empty() ||
submaps_.back()->num_range_data() == options_.num_range_data() )
// 删除旧子图,加入新子图。 参数是局部坐标系中的位姿 x y
// 新子图的初始位置,为起始range的激光坐标
// 也就是说num_range_data个scan,只取第1个scan的初始位置
AddSubmap(range_data.origin.head<2>());
for (auto& submap : submaps_ )
submap->InsertRangeData(range_data, range_data_inserter_.get() );
if (submaps_.front()->num_range_data() == 2 * options_.num_range_data())
submaps_.front()->Finish();
return submaps();
}
先看AddSubmap1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void ActiveSubmaps2D::AddSubmap(const Eigen::Vector2f& origin)
{
if (submaps_.size() >= 2)
{
// 在插入新子图之前,crop the finished Submap
// 以减少内存的占用。 保证只有两个子图
CHECK(submaps_.front()->insertion_finished());
submaps_.erase(submaps_.begin() ); // 删除旧子图,但对象没有销毁
}
submaps_.push_back( absl::make_unique<Submap2D>(
origin,
std::unique_ptr<Grid2D>(
static_cast<Grid2D*>(CreateGrid(origin).release()) ),
&conversion_tables_) );
}
注意删除的旧子图是begin()头,保留的是back()尾。 此时头有2N个scan,尾有N个scan。erase头之后,因为调用的是push_back,所以之前的尾变成了新的头,新的尾此时没有scan。 添加submap时记录了它在local map坐标系下的位置local_pose_, 以及Grid的限制条件,比如分辨率,长宽,最大值。 CreateGrid在下面讲解。
也就是逻辑如下:
在拥有两个子图后,头部的子图总比尾部多N个scan。 在ScanMatch里会看到,头部的子图(旧图)用于 real_time_correlative_scan_matcher
Submap2D 和 Grid2D
它是ActiveSubmaps2D中维护的子图数据类型, 该数据类型继承自Submap。父类Submap定义了2D和3D子图的一些共有的属性,该类主要描述了子图在local坐标系下的相对位姿,记录插入的数据数量以及是否构建完成等基本信息。
Submap的成员变量如下:1
2
3const transform::Rigid3d local_pose_; // 子图在local坐标系的位姿
int num_range_data_ = 0; // 子图中插入的数据数量
bool insertion_finished_ = false; // 标志着子图是否已经构建完成Submap2D类增加一个很重要的成员变量grid_, 类型Grid2D,用于保存子图的详细信息,比如概率栅格的占用情况,子图的大小等。成员变量如下: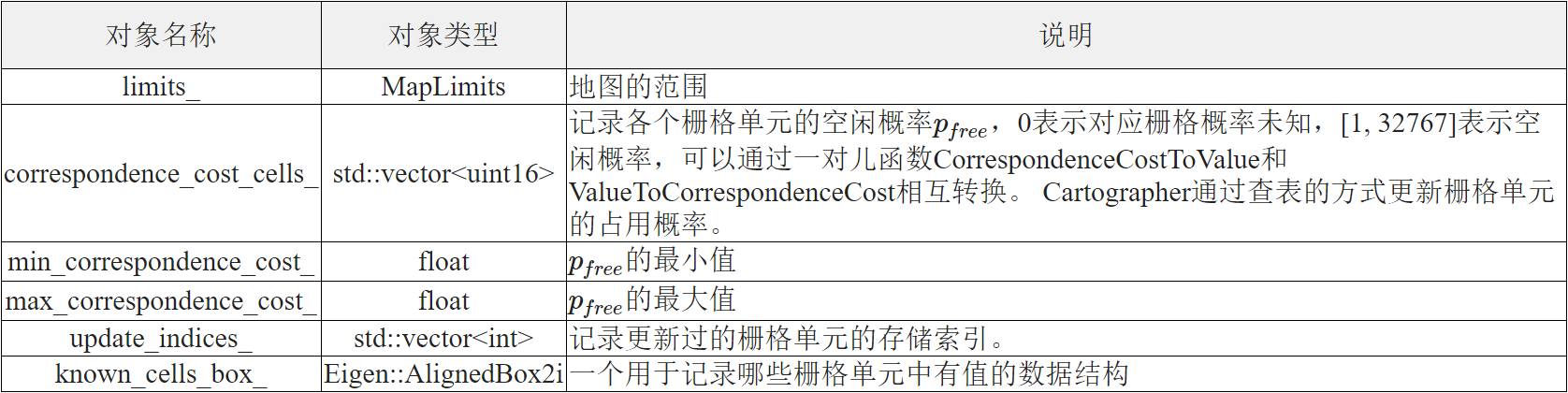
最重要的是 correspondence_cost_cells_:地图栅格值,存储free概率转成uint16后的[0, 32767]范围的值,0代表未知
value_to_correspondence_cost_table_: 将[0, 1~32767] 映射到 [0, 0.1~0.9] 的转换表update_indices_记录已经更新过的索引
函数CreateGrid用于为子图创建栅格信息存储结构。在获取了子图尺寸和分辨率信息之后,就构建了一个ProbabilityGrid类型的栅格存储。(一般不用TSDF格式)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16std::unique_ptr<GridInterface> ActiveSubmaps2D::CreateGrid(
const Eigen::Vector2f& origin)
{
constexpr int kInitialSubmapSize = 100;
float resolution = options_.grid_options_2d().resolution();
// 省略TSDF格式
// 构建了一个ProbabilityGrid 类型的栅格存储
return absl::make_unique<ProbabilityGrid>(
MapLimits(resolution,
origin.cast<double>() + 0.5 * kInitialSubmapSize * resolution *
Eigen::Vector2d::Ones(),
// CellLimits函数只有赋值给成员 num_x_cells和num_y_cells
// 只保证num_x_cells和num_y_cells大于0
CellLimits(kInitialSubmapSize, kInitialSubmapSize) ),
&conversion_tables_ );
}MapLimits用于描述地图的范围,它有三个成员变量
MapLimits第2个参数是max,记录了地图的x和y方向上的最大值( 地图坐标系的左上角 )。这样origin就在submap的中心,保证该submap和上一个submap有足够重合的部分,最终建成的子图列表是这样的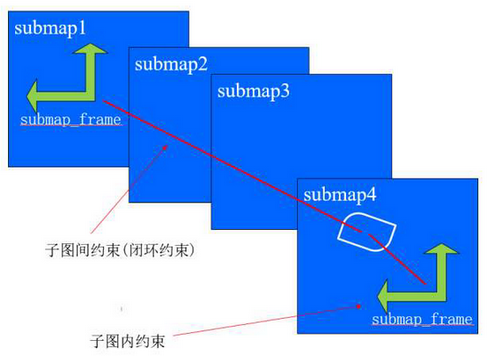
Submap2D::InsertRangeData
回头还看InsertRangeData,发现出现了一个Submap2D::InsertRangeData1
2
3
4
5
6
7
8
9void Submap2D::InsertRangeData(
const sensor::RangeData& range_data,
const RangeDataInserterInterface* range_data_inserter)
{
CHECK(grid_);
CHECK(!insertion_finished());
range_data_inserter->Insert(range_data, grid_.get());
set_num_range_data(num_range_data() + 1);
}
它是将激光的扫描数据插入到grid_对象中,在调用该函数之前需要确保子图更新还没有结束。其实有用的就一句:range_data_inserter->Insert(range_data, grid_.get());,实际调用的是ProbabilityGridRangeDataInserter2D::Insert,这个函数看另一篇文章:处理子图 3. CastRays和更新栅格概率