导数的定义是这样的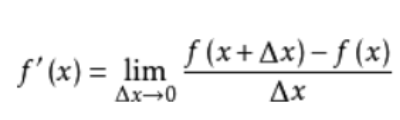
SLAM问题会构建一个优化问题,求解最优的R t,使误差最小化。这必然涉及求导,SLAM的运动过程是连续的,所以一定是可以求导的。在SLAM中最常见的变换是四维变换矩阵T以及三维旋转矩阵R。但是它们对加法并不封闭: 两个变换矩阵之和明显不是变换矩阵;而旋转矩阵是正交矩阵,但两个正交矩阵之和不是正交矩阵。需要把函数f换成旋转矩阵R,对自变量添加一个微小值来进行,但是前面我们说了,旋转矩阵做加减法运算之后就不再满足旋转矩阵的形式了,没有加减法就意味着不能求导了。
为什么会出现李群李代数的概念,原因就在于此。SLAM应当能求导,只是我们不该用这两种矩阵的形式,而是用李代数。
另外两个原因:
- 旋转矩阵都是正交矩阵且行列式为1,它们作为优化变量时,会引入额外的约束,使优化更困难了。
- 优化变量的迭代阶段: 不能直接用两种矩阵相加
引入李群和李代数,就可以解决旋转矩阵求导问题,也就是说李代数se(3)和so(3)对加法封闭,所以用李代数表示机器人的旋转和位移。求导结束后,再对数映射为李群,这个过程都是由优化器完成的,无需我们手动。
李群和李代数
具有连续(光滑)性质的群。整数群是离散的,没有连续性质。SO(3)和SE(3)都是连续的,空间中的机器人的姿态是连续变化的,而不是磕磕绊绊地运动,所以都是李群。
机器人的旋转是一个随时间连续变化的过程,函数是R(t),根据旋转矩阵的性质
经过一系列推导,发现 是一个反对称矩阵,因此写做
这里的 是一个三维向量,对应到 SO(3) 的李代数 ,李群和李代数直接是指数映射。
假设在很小的时间范围内, 是一个恒定值,因为实际中机器人的姿态并不会突变。再经过一系列推导得到
李代数包括一个集合,一个数域和一个二元运算符,它们满足四条性质:封闭性、双线性、自反性、雅克比等价。
在不引起歧义的情况下,我们说李代数的元素是三维向量或3维反对称矩阵,不做区别。
对于李群SE(3),对应的李代数 每个元素是一个6维向量,前三维是平移,后三维是旋转,实际就是 元素。 此时的 符号是把6维向量转换为四维的变换矩阵 T
对于李代数 的元素 ,由于它是3维向量,写成 , 是和 方向相同的单位向量, 是 的模长。
经过一连串推导,获得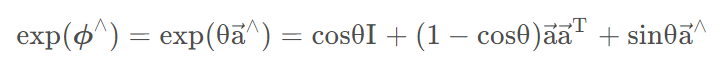
这实际就是罗德里格斯公式 3.14.
旋转矩阵的李代数实际上就是旋转向量组成的空间。指数映射其实就是通过罗德里格斯公式变换的。
BCH公式

根据BCH公式,第2个公式右边还有一些余项
李代数的求导问题
对于公式 4.39,需要计算目标函数J关于变换矩阵T的导数。我们经常构建与位姿有关的函数,然后讨论该函数关于位姿的导数,以调整当前的估计值。但是旋转矩阵和变换矩阵,它们对加法都没有良好的定义,所以对姿态有关的函数求导,只能通过李代数进行。关于用李代数解决求导问题,有两种思路:
- 用李代数表示姿态,然后根据李代数加法对李代数进行求导
- 对李群左乘或者右乘微小扰动,然后对该扰动求导。即左扰动和右扰动模型。
因为旋转矩阵没有加法,所以我们就对旋转矩阵的李代数就行求导,也就是李代数的局部坐标上添加扰动,由于李代数本身对应旋转向量,因此对旋转向量添加扰动相当于同时改变旋转轴和旋转角度。
对一个空间点进行旋转,得到,现在计算旋转后的点坐标相对旋转的导数,不严谨地记做
由于没有加法,假设对应的李代数为,于是我们计算出
平时不用这种方法,而是用扰动模型法。
不管是李代数求导还是扰动模型,都是旋转矩阵对李代数的求导。
对R进行一次扰动 ,这个扰动可以乘在 左边,也可以是右边。假设 对应的李代数为 ,然后对 求导
- 左扰动模型
- 右扰动模型
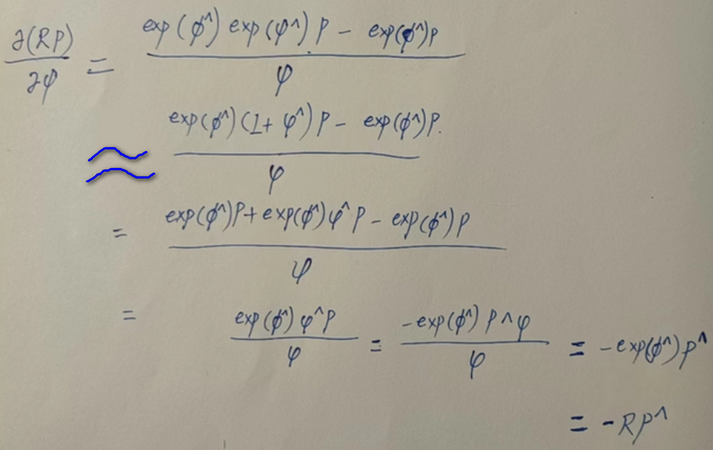
扰动模型,显然计算量上要少非常多。
