机器人SLAM问题中涉及到平移和旋转，平移是在欧氏空间中，连续的平移变换只需要向量相加。 可是旋转是在非欧空间了，连续的旋转变换就是矩阵连续右乘

右手坐标系：x向前(roll)，y向左(pitch)，z向上(yaw)

用矩阵表示绕某轴旋转

旋转矩阵

坐标系A变换到B，从坐标系B到坐标系A的旋转矩阵的每一列，都是{B}的坐标轴单位向量在{A}中的表示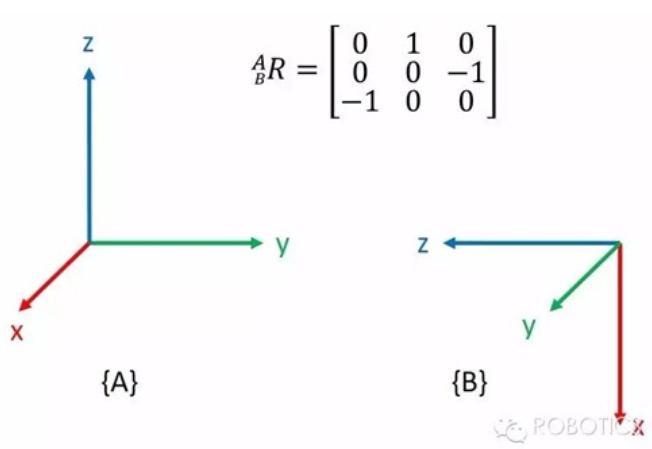

旋转矩阵R是一个行列式为1的正交矩阵，而且行向量和列向量的长度都为1，所以它的转置就是它的逆，而逆矩阵就可以将坐标系旋转回来。
R的每一行就是{A}的坐标轴单位向量在{B}中的表示。
SO(n)是特殊正交群，这个集合由n维空间的旋转矩阵组成。 SO(3)指三维空间的旋转。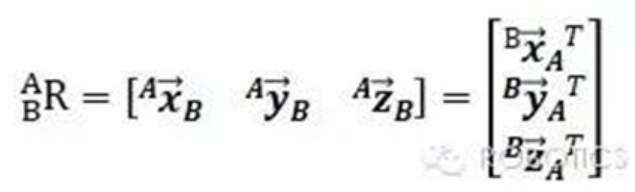

变换矩阵

$$T =\left[ \begin{matrix} R & t \\ 0 & 1 \\ \end{matrix} \right]$$

左上角为旋转矩阵，右侧为平移向量，这种矩阵又称为特殊欧氏群

$$SE(3) = \left \{T =\left[ \begin{matrix} R & t \\ 0 & 1 \\ \end{matrix} \right] \in \mathbb{R}^{4\times4} \ | R\in SO(3), t\in \mathbb{R}^3 \right \}$$

逆矩阵的形式 $\left[ \begin{matrix} R & t \\ 0 & 1 \\ \end{matrix} \right]^{-1} \ = \left[ \begin{matrix} R^T & -R^Tt \\ 0 & 1 \\ \end{matrix} \right]$

如果一个点的坐标是 $P(x,y,z)$，那么点作T变换后的坐标就写作 $R*P + t$，按齐次矩阵和坐标形式计算就可得到。

Censi 公式

我习惯用Censi论文的公式，还可以用Grisetti派系的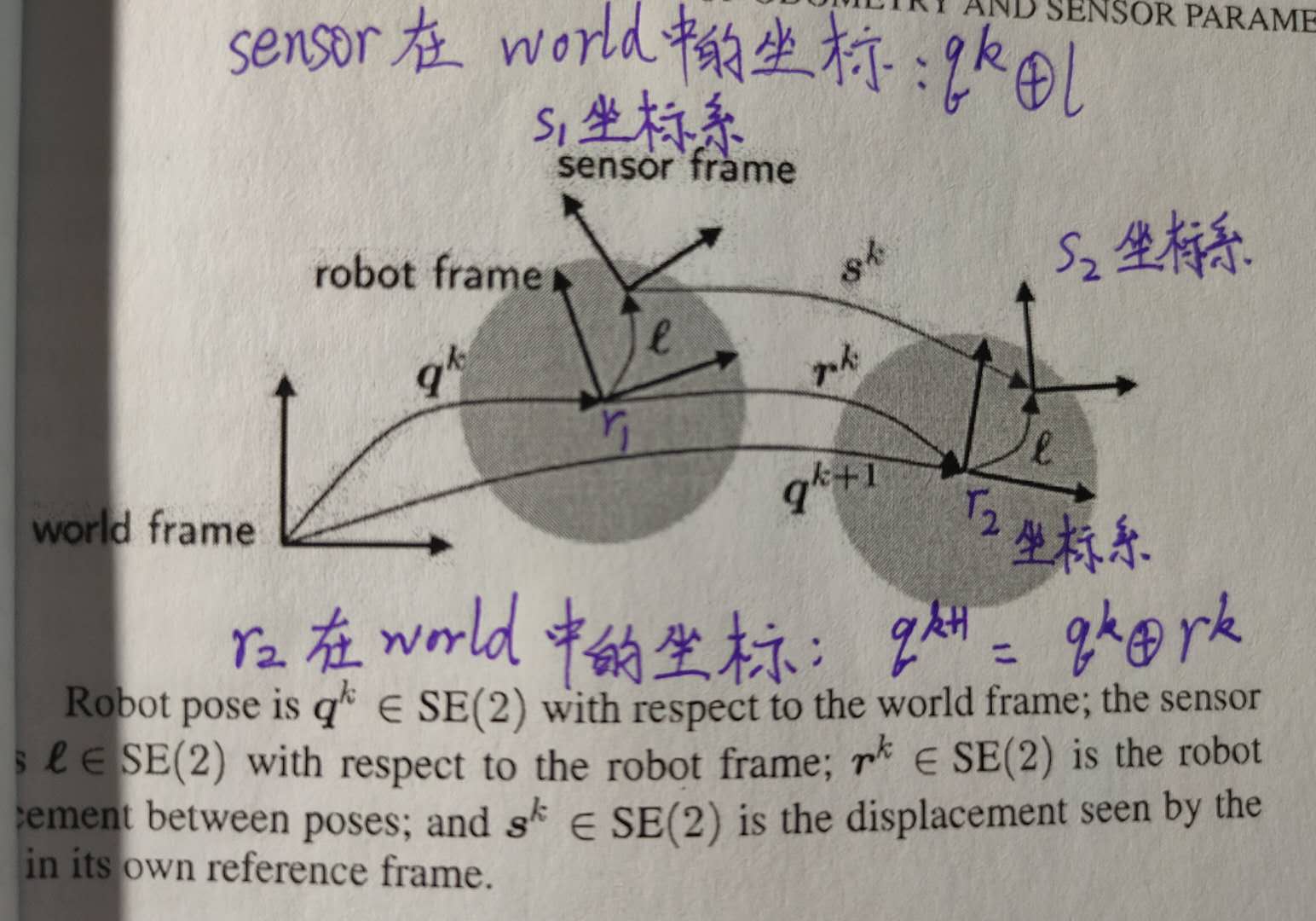

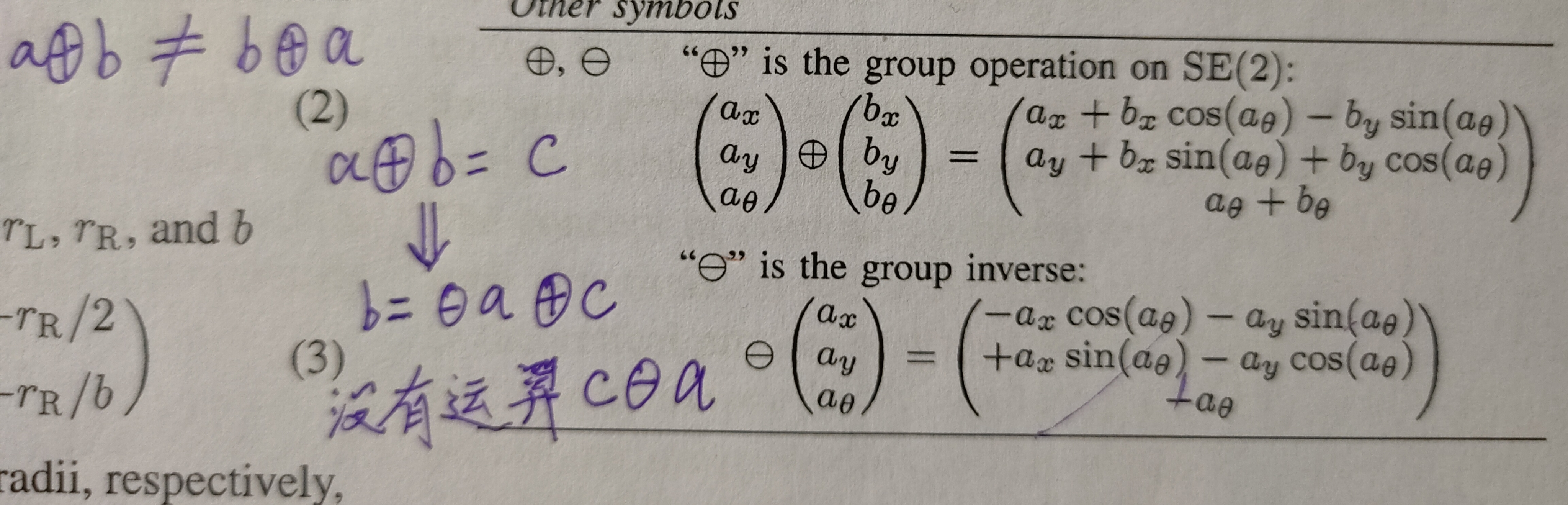
$$\quad\quad\quad\quad\quad\quad \vec{a} \oplus \vec{b} = \vec{c}$$

$\quad\quad\quad\quad\quad\quad\quad\Downarrow$

$$\begin{pmatrix} a_x \\ a_y \\ a_{\theta} \end{pmatrix} + \left[ \begin{matrix} cos_{a_\theta} & -sin_{a_\theta} & 0 \\ sin_{a_\theta} & cos_{a_\theta} & 0 \\ 0 & 0 & 1\end{matrix} \right] * \begin{pmatrix} b_x \\ b_y \\ b_{\theta} \end{pmatrix} = \begin{pmatrix} c_x \\ c_y \\ c_{\theta} \end{pmatrix}$$

其实这里就是 $Rp + t$ ，只是在二维平面，R就是绕Z轴旋转的旋转矩阵形式。

左乘和右乘

左乘是行变换，右乘是列变换。这是因为习惯上来说，空间中的向量用列向量表示，用矩阵左乘列向量，就是把它在空间当中变换。

若绕静坐标系（世界坐标系）旋转，则左乘，也是变换矩阵 x 坐标矩阵。 在固定坐标系下，一个点 $p$ 经过一个旋转矩阵$R_1$，再经过一个旋转 $R_2$ ，总共旋转 $R_2 * R_1 * p$，这是左乘。 向量旋转中的右乘本没必要，甚至会引起人误解。

若是绕动态坐标系旋转（自身建立一个坐标系），则右乘，也就是坐标矩阵 x 变换矩阵。

即左乘是相对于坐标值所在的坐标系（世界坐标系）下的三个坐标轴进行旋转变换，右乘则是以当前点为旋转中心，进行旋转变换。

车在全局坐标系中运动，这可以看做绕固定轴旋转的过程，是左乘矩阵

具体去看文章： 欧拉角，旋转矩阵，旋转向量，四元数

图优化里的相对位姿是由右乘获得的，即节点 $X_i$ 和 $X_j$ 之间的相对位姿是

$$Z_{ij} = X_i^{-1}*X_j$$

常用的公式 $P_c=R_c∗P_w+t_c$ 是把点P从$w$坐标系转换到 $c$ 坐标系，由于旋转时，两个坐标系原点还是重合的，我们说经过了平移后，平移向量 $t_c$ 是从坐标系 $w$坐标系指向 $c$

参考：
cartographer中公式的推导