以下面的加权图举例，说明算法的过程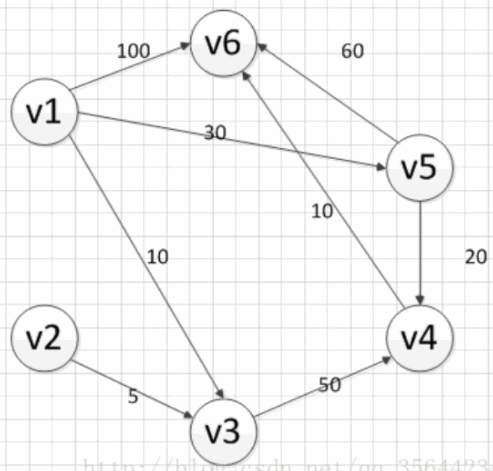

加权图中不可有负权边

或者这样理解：

1. 第一个核心步骤：找到当前未处理过的顶点中 $L_k$最小的点 V，（由于起点到起点的消耗为0，所以算法开始时 V 必定代表起点）；
2. 第二个核心步骤：若V有邻居，则计算经过 V 的情况下起点到达各邻居的消耗 $L$，并选择是否更新 V 邻居的$L_k$值。若没有邻居则对该点的处理结束
3. 重复以上两个核心步骤，直到满足算法终止的条件：有向图中所有的点都被处理过。

算法每处理完一个顶点后，该顶点对应的 $L_k$值就是起点到该点的最短路径长度，且$L_k$在这之后不会被更改。这就是最短路径的原因

Dijkstra的特点是从起点开始，由近及远，层层扩展。越靠前处理的点离起点越近，最后一个处理的点离起点最远。
即使我只想找两个点之间的最短路径，Dijkstra还是需要遍历所有节点，因此时间复杂度为$O(n^2)$，所以不适合复杂路径等大规模场景。