Eigen(三) 欧氏变换，cholesky，SVD，最小二乘

欧氏变换

欧氏变换(Isometry Transform)可以看作是维持任意两点距离不变的变换，在实际场景中使用比较多。在Eigen中已经内置好了一些常用的欧氏变换:

typedef Transform<float,2,Isometry> Isometry2f;
typedef Transform<float,3,Isometry> Isometry3f;
typedef Transform<double,2,Isometry> Isometry2d;
typedef Transform<double,3,Isometry> Isometry3d;

欧氏变换必须初始化，如果没初始化，Isometry3d中的元素全为0，一般初始化为单位矩阵，也可以初始化为Quaternion。赋值可以通过它的成员函数.rotate()和.translate()完成

AngleAxisd rotation(3.1415926 / 4, Vector3d(1, 0, 1).normalized());
Vector3d translation(1, 3, 4);
Isometry3d T= Isometry3d::Identity();
// 先平移后旋转
T.translate(translation);
T.rotate(rotation);

A.translate(B)等价于A×B，而A.pretranslate(B)等价于B×A，对应于左乘和右乘的区别。凡是前面带pre的函数，其变化都是相对于上一步变化之前的状态进行的。举例说我要新建一个按固定轴先平移后旋转的变换。但我首先设置了旋转，然后再设置平移。这个时候设置平移就不能用translate()了，而应该用pretranslate()。因为第一步已经对坐标系进行了旋转，后面的平移是在旋转后的坐标系中进行的，所以最好不要用pre开头的函数

针对求解Ax = b这种线性问题，Eigen提供了下面几种分解方法，每一种方法都提供了一个solve()函数以便求解得到 x，Eigen对每一种分解方法的速度和精度做了如下对比。当然对于小矩阵，各个方法没什么区别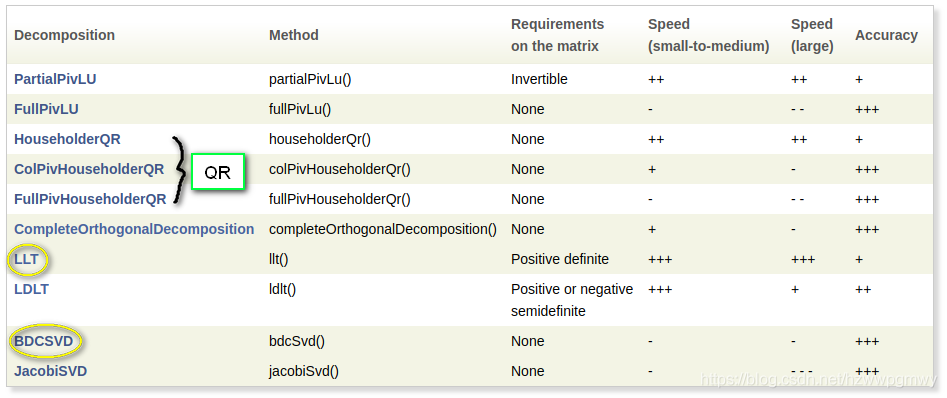

LLT(cholesky)是最快的求解器，但是精度也是最差的，并且只能对正定矩阵进行分解，而LDLT则可以应对正半定和负半定问题，精度较LLT更高，所以尽量使用LDLT，但是LDLT在求解大矩阵问题时，耗时较QR增加更多，所以究竟选择那种分解方式求解问题，需要根据速度和精度综合考量

使用info()判断是否收敛

1
2
3

SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
if (eigensolver.info() != Success)
    abort();

对于自伴随矩阵，Eigen使用SelfAdjointEigenSolver进行特征值分解

Eigen::SelfAdjointEigenSolver< Eigen::Matrix3d > eigen_solver( matrix_33 );
// 特征值   特征向量
cout << "Eigen values = " << eigen_solver.eigenvalues( ) << endl;
cout << "Eigen vectors = " << eigen_solver.eigenvectors( ) << endl;

cholesky 分解

Cholesky分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。Eigen的LLT分解实现了Cholesky分解。代码如下：

#include<Eigen/Cholesky>
int main(int argc, char** argv)
{
   Eigen::Matrix2d down;
   down<<1,0,
         2,1;
   // A <<1,2
   //   2,5
   Eigen::Matrix2d A = down*down.transpose();
   std::cout<<"A: "<< A <<std::endl;
   // 直接用 llt() 函数
   Eigen::Matrix2d ml = A.llt().matrixL();
   Eigen::Matrix2d testA = ml*ml.transpose();

   std::cout<<"mllt:   "<< ml<<std::endl;
   std::cout<<"testA:  "<<testA<<std::endl;
  return 0;
}

对于Ax=b，LLT分解并不会检查 A 矩阵的对称性，所以如果你输入的 A 矩阵不是正定的Hermite矩阵，你也会得到分解结果，只不过是错误的

LDLT分解

LDLT分解法实际上是Cholesky分解法的改进，优先使用LDLT而不是LLT方法。 Cholesky分解法虽然不需要选主元，但其运算过程中涉及到开方问题，而LDLT分解法则避免了这一问题。仍然要求A矩阵正定。 其中L为下三角形单位矩阵(即主对角线元素皆为1，下三角其他元素不为0)，D为对角矩阵， $L^T$ 为L的转置矩阵。

Matrix2f A, b;
A << 2, -1, -1, 3;
b << 1, 2, 3, 1;
cout << "Here is the matrix A:\n" << A << endl;
cout << "Here is the right hand side b:\n" << b << endl;
Matrix2f x = A.ldlt().solve(b);
cout << "The solution is: \n" << x << endl;

QR分解

Matrix3f A;
Vector3f b;
A << 1,2,3,  4,5,6,  7,8,10;
b << 3, 3, 4;
// 返回一个类ColPivHouseholderQR的对象
Vector3f x = A.colPivHouseholderQr().solve(b);
cout << "The solution is:\n" << x << endl;

SVD分解 - 奇异值分解

特征值分解仅针对方阵，而不是方阵的矩阵就有了SVD分解： $A=U\Sigma V^T$
其中A为m x n的矩阵，正交矩阵 U(m x m阶) 和 V(n x n阶)。

$\Sigma_{mn} = \left[ \begin{matrix} \Sigma_1 & t \\ 0 & 1 \\ \end{matrix} \right]$ $\Sigma_1=diag(\sigma_1....\sigma_r)$

矩阵U的列称为左奇异向量, 是正交的。矩阵V的列向量(也称为右奇异向量)也是正交的.

此时的A如果是方阵，那么逆矩阵也很容易求出: $A^{-1} = VD^{-1}U^T$
奇异值分解同时包含了旋转、缩放( $\Sigma$ )和投影三种作用。特征值分解只有缩放的效果。

Eigen::Matrix3f A;
A << 3,4,2,
     1,2,4,
     8,0,1;
// SVD分解
Eigen::JacobiSVD<Eigen::Matrix3f> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);
// 求出三个矩阵
Eigen::Matrix3f U = svd.matrixU();
Eigen::Matrix3f V = svd.matrixV();
// 推荐方法，从对角线元素组成的向量直接构造对角矩阵
Eigen::Matrix3f diag = svd.singularValues().asDiagonal();

cout << "U: "<<endl<< U <<endl<<endl;
cout << "V transpose: "<< endl << V.transpose() <<endl<<endl;
cout << "Sigma from SVD: "<< endl << diag<<endl<<endl;

// 判断U和V是否正交矩阵（酉矩阵），和转置的乘积为单位矩阵
cout << U.isUnitary() <<endl<<endl;
cout << V.isUnitary() <<endl<<endl;
cout <<"***********************"<<endl;

// 从公式推导出的对角矩阵，有误差
Eigen::Matrix3f Sigma = U.inverse() * A * V.transpose().inverse();
cout << "Sigma from formula: "<< endl << Sigma <<endl<<endl;

// 大致等于原矩阵A
cout<< "A from formula: "<< endl <<U *Sigma *V.transpose()<<endl;

运行结果:


U: 
   0.4853 -0.514629 -0.706853
 0.299358 -0.661777   0.68734
 0.821504  0.545168  0.167102

V transpose: 
  0.904647   0.275928   0.324773
  0.423663  -0.664689  -0.615385
-0.0460712    -0.6943    0.71821

S from SVD: 
9.20501       0       0
      0  5.0882       0
      0       0 2.09237

1

1
***********************
S from formula: 
     9.20501 -9.53674e-07 -2.38419e-07
 -1.3113e-06       5.0882  1.05798e-06
-7.15256e-07  2.90573e-07      2.09237

A from formula: 
3 4 2
1 2 4
8 0 1

Eigen提供了两个类以实现SVD分解：BDCSVD（大矩阵）和JacobiSVD（小矩阵），推荐使用BDCSVD，因为当发现要分解的矩阵是小矩阵时，将自动切换到JacobiSVD

A转为正交矩阵

把上面的ComputeFullU换成ComputeThinU，那么 $U \times V^T$ 就是一个正交矩阵B

// SVD分解, ComputeThin参数时，A必须是 Eigen::MatrixXf
Eigen::JacobiSVD<Eigen::MatrixXf> svd(A, Eigen::ComputeThinU | Eigen::ComputeThinV );
// 求出三个矩阵，这样B就是个正交矩阵
Eigen::Matrix3f U = svd.matrixU();
Eigen::Matrix3f V = svd.matrixV();
Eigen::Matrix3f B = U * V.transpose();

cout << B.transpose() << endl <<endl;
cout << B.inverse() << endl<<endl;

线性方程组的最小二乘解

如果一个线性方程组是超定的(overdeterminated，未知数个数>方程数)，这时候常规方法无解，就需要用最小二乘拟合最优结果。最精确的解法是SVD分解。SVD也有多种解法，官方推荐的是BDCSVD方法。

如下超定方程组：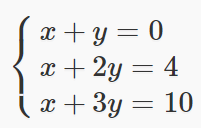

最小二乘求解代码如下：

MatrixXf A(3, 2);
Vector3f b;
Vector2f x;
A << 1,1, 1,2, 1,3 ;
b << 0,4,10;
x = A.bdcSvd(ComputeThinU | ComputeThinV).solve(b);
cout << x << endl;

Vector3f error = (A*x - b).cwiseAbs();
double mean_error = error.mean();

程序运行需要一点时间，最后得到的x就是通过最小二乘算出来的。这里bcdScd()函数里面的参数ComputeThinU | ComputeThinV必须要写(可以先记住)，否则会报错。

将得到的解带回方程会发现其并不是严格成立的，有时可能还会相差较大。这是因为对于超定方程，采用最小二乘法得出的解并不一定对每一个方程都严格成立，其确保的是当前解在所有方程上的总误差最小。得到解以后我们可以反算出其解的整体精度

对于小矩阵，逆矩阵和行列式随便算，如果是大矩阵，计算量会很庞大。确定你是否真的需要逆矩阵，因为很多时候求逆矩阵都是为了求解Ax = b问题，所以最好使用上面介绍的分解方法代替.

参考：
Eigen学习与使用笔记
 Eigen学习与使用笔记2
Eigen官方文档-AngleAxis
矩阵的特征分解与奇异值分解