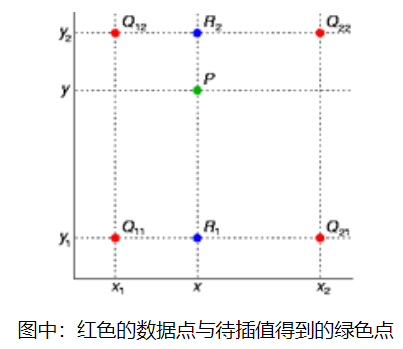
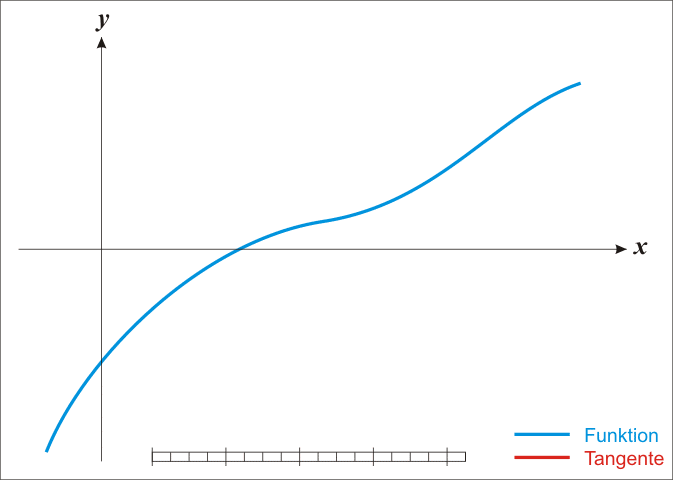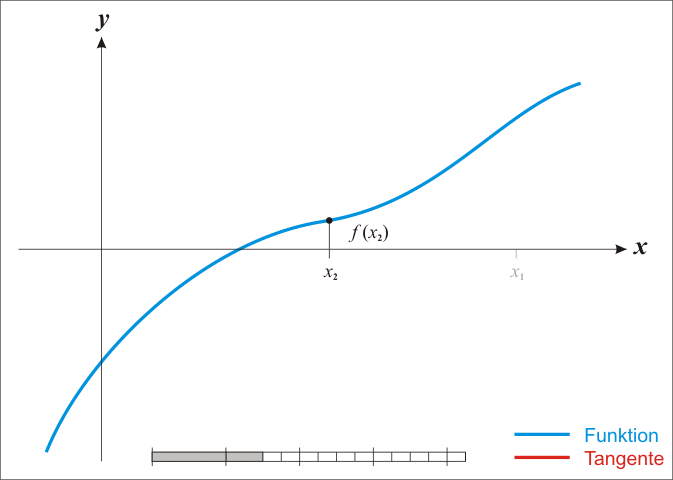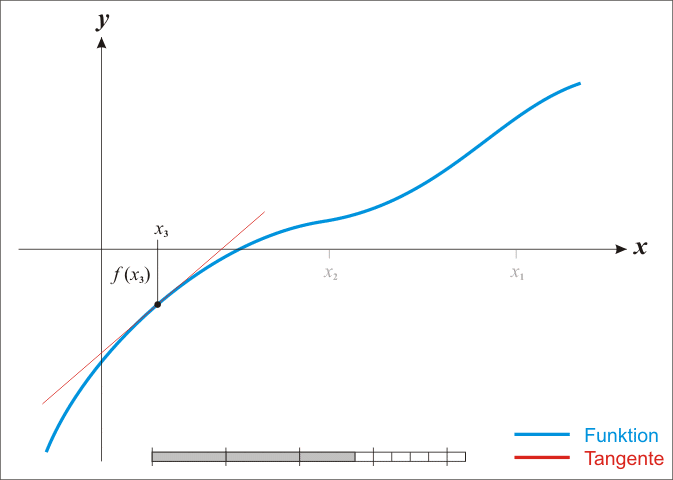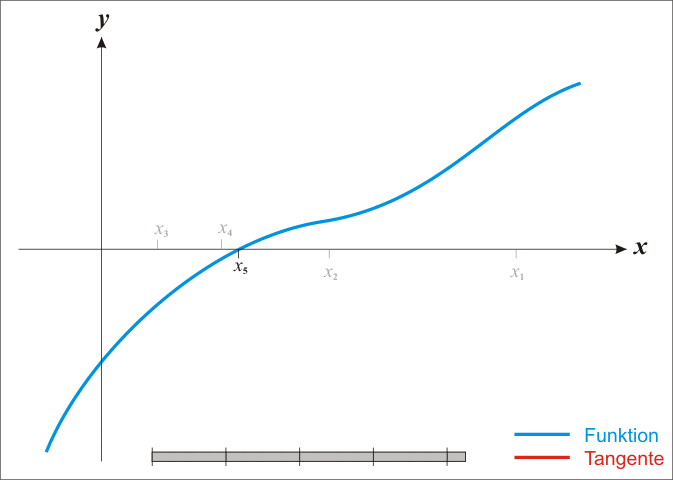
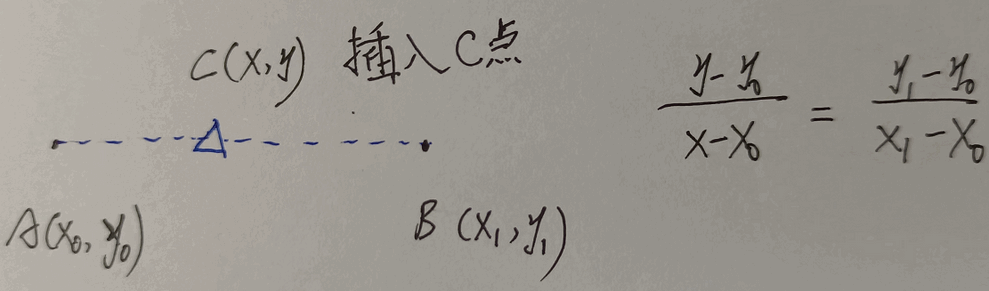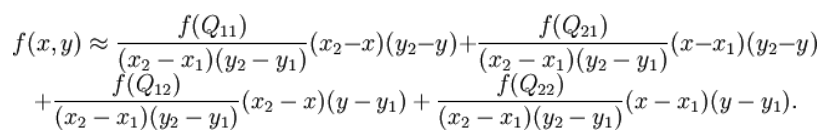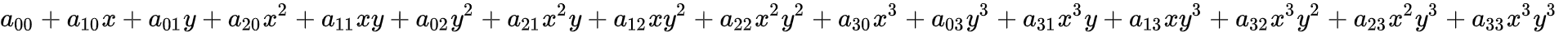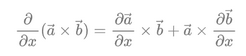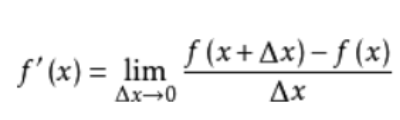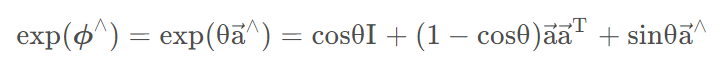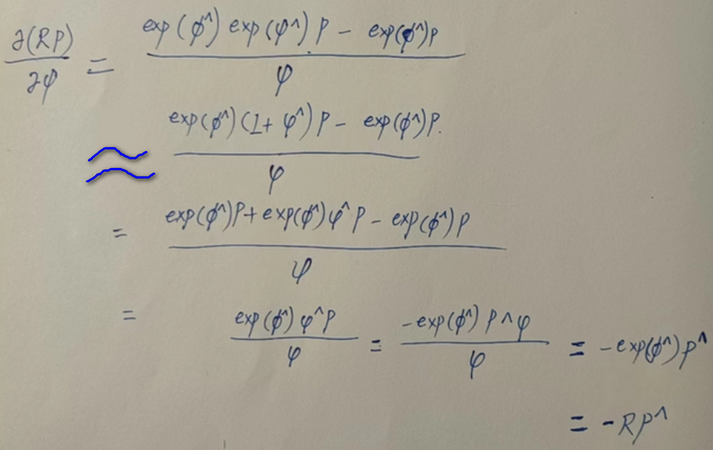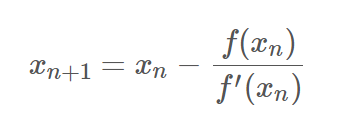后端 4 计算约束的准备工作|激光SLAMCartographer源码解读

接上一篇，看两次计算约束的函数 ComputeConstraint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 根据指定的 nodeid 和 submapid 计算其约束
void PoseGraph2D::ComputeConstraint(const NodeId& node_id,
                                    const SubmapId& submap_id)
{
  bool  maybe_add_local_constraint = false;
  bool  maybe_add_global_constraint = false;
  const  TrajectoryNode::Data*  constant_data;
  const  Submap2D* submap;
  {
    absl::MutexLock locker(&mutex_);
    CHECK(data_.submap_data.at(submap_id).state == SubmapState::kFinished);
    if (!data_.submap_data.at(submap_id).submap->insertion_finished() )
    {
      // Uplink server only receives grids when they are finished,
      // so skip constraint search before that.
      return;
    }
    // 获取两个id最新的那个时刻
    const common::Time  node_time = GetLatestNodeTime(node_id, submap_id);
    const common::Time  last_connection_time =
        data_.trajectory_connectivity_state.LastConnectionTime(
            node_id.trajectory_id,  submap_id.trajectory_id );
    // 如果节点与submap在同一轨迹内或者距离上次全局约束时间较短，则计算局部约束
    if (node_id.trajectory_id == submap_id.trajectory_id ||
        node_time <
            last_connection_time +
                common::FromSeconds(
                    options_.global_constraint_search_after_n_seconds()) )
    {
        maybe_add_local_constraint = true;
    }
    // 如果不在同一轨迹内，一定间隔计算全局约束
    else if (global_localization_samplers_[node_id.trajectory_id]->Pulse() )
    {
        maybe_add_global_constraint = true;
    }
    constant_data = data_.trajectory_nodes.at(node_id).constant_data.get();
    submap = static_cast<const Submap2D*>(
        data_.submap_data.at(submap_id).submap.get()  );
  }

  • 建图模式，节点与submap在同一轨迹内 或者 存在一个最近的全局约束把节点的轨迹和子图的轨迹连接起来时，使用local search window计算局部约束；

  • 纯定位模式，节点与submap不在同一轨迹，使用全局搜索窗口计算约束(对整体子图进行回环检测) 。纯定位进行慢，主要就是 global_constraint_search_after_n_seconds 较大导致，迟迟不能确认maybe_add_global_constraint为true

local约束在求解时，搜索窗口小，有初值;    global约束在求解时，搜索窗口大，没有初值。 记住二者都是计算 Constraint::INTER_SUBMAP

准备计算局部和全局约束

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if (maybe_add_local_constraint)
{
  const transform::Rigid2d  initial_relative_pose =
      optimization_problem_->submap_data()
          .at(submap_id)
          .global_pose.inverse() *
      optimization_problem_->node_data().at(node_id).global_pose_2d;
  // 添加局部约束，进行闭环匹配，更新相对位置
  constraint_builder_.MaybeAddConstraint(
      submap_id, submap, node_id, constant_data, initial_relative_pose);
}
  // 添加全局约束
else if (maybe_add_global_constraint)
  constraint_builder_.MaybeAddGlobalConstraint(
      submap_id, submap, node_id, constant_data);

前端得到节点相对于世界的位姿，也可以得到某个子图的世界位姿，因此得到这个节点相对于这个子图的相对位姿，把这个位姿称为 初始位姿 1。 之所以要用世界坐标系作为桥梁，是因为子图和这个节点并不一定在在同一条轨迹坐标系中(local map坐标系)

这里主要是ConstraintBuilder2D类的两个函数: MaybeAddConstraint 和 MaybeAddGlobalConstraint，它们只有细微不同，前者的开头有这样两句：

1
2
3
if (initial_relative_pose.translation().norm() >
      options_.max_constraint_distance()  )
    return;

然后就是其中调用的ConstraintBuilder2D::ComputeConstraint不同，局部约束的是 ComputeConstraint(submap_id, submap, node_id, false, constant_data, initial_relative_pose, *scan_matcher, constraint);

全局约束的是 ComputeConstraint( submap_id, submap, node_id, true, constant_data, transform::Rigid2d::Identity(), *scan_matcher, constraint);，也就是 match full submap

局部约束

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void ConstraintBuilder2D::MaybeAddConstraint(
    const SubmapId& submap_id,  const Submap2D* const submap,
    const NodeId& node_id, 
    const TrajectoryNode::Data* const constant_data,
    const transform::Rigid2d& initial_relative_pose)
{
  // 参数  max_constraint_distance
  // 初始位姿 1 的模不能太大
  // 约束并非无限制距离，若子图和节点的距离太远，则无需考虑约束
  if (initial_relative_pose.translation().norm() >
      options_.max_constraint_distance() )
        return;
  /* 这是 ConstraintBuilder2D类 唯一使用采样器的地方
  ratio 默认 0.3， 参数 sampling_ratio
  sampling_ratio越小， Pulse()返回的false越多，更容易return*/
  if (!sampler_.Pulse()) return;

  absl::MutexLock locker(&mutex_);
  // std::unique_ptr<std::function<void(const Result&)>>  when_done_;
  if (when_done_)
  {
    LOG(WARNING)
        << "MaybeAddConstraint was called while WhenDone was scheduled.";
  }
  constraints_.emplace_back();  // 添加空元素
  kQueueLengthMetric->Set(constraints_.size()  );
  // 指针指向，对最后一个元素赋值
  auto* const constraint = &constraints_.back();
  // fast time scan matcher 在这里
  const auto* scan_matcher = 
      DispatchScanMatcherConstruction(submap_id, submap->grid()  );
}

参数max_constraint_distance很重要，如果建图回到同一位置，但没有出现回环，可能是因为过程中的累计误差过大了，大于这个参数，导致没有求 inter 约束。

DispatchScanMatcherConstruction

针对某一个submap_id的submap构建一个扫描匹配器,先看返回类型

1
2
3
4
5
6
7
8
struct SubmapScanMatcher
{
  const Grid2D* grid = nullptr;
  std::unique_ptr<scan_matching::FastCorrelativeScanMatcher2D>
      fast_correlative_scan_matcher;
  // 线程池用的 Task
  std::weak_ptr<common::Task>  creation_task_handle;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const ConstraintBuilder2D::SubmapScanMatcher*
ConstraintBuilder2D::DispatchScanMatcherConstruction(
      const SubmapId& submap_id,  const Grid2D* const grid)
{
  CHECK(grid);
  if (submap_scan_matchers_.count(submap_id) != 0)
      return &submap_scan_matchers_.at(submap_id);

  // Map of dispatched or constructed scan matchers by 'submap_id'
  // std::map<SubmapId, SubmapScanMatcher>  submap_scan_matchers_
  auto& submap_scan_matcher = submap_scan_matchers_[submap_id];
  // 下面都是成员赋值
  submap_scan_matcher.grid = grid;
  auto& scan_matcher_options = options_.fast_correlative_scan_matcher_options();

  auto scan_matcher_task = absl::make_unique<common::Task>();
  // 这里也是 work_item 机制
  scan_matcher_task->SetWorkItem(
      [&submap_scan_matcher, &scan_matcher_options]() {
        submap_scan_matcher.fast_correlative_scan_matcher =
            absl::make_unique<scan_matching::FastCorrelativeScanMatcher2D>(
                *submap_scan_matcher.grid, scan_matcher_options);
      } );

  submap_scan_matcher.creation_task_handle = 
      thread_pool_->Schedule(std::move(scan_matcher_task));
  return &submap_scan_matchers_.at(submap_id);
}

这里就是构造了scan_matcher_task的 work_item，返回 scan_matcher。

继续看MaybeAddConstraint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 // 线程池
auto constraint_task = absl::make_unique<common::Task>();
constraint_task->SetWorkItem([=]() LOCKS_EXCLUDED(mutex_)
{
  ComputeConstraint(submap_id, submap, node_id, false, /* match */
                    constant_data, initial_relative_pose, *scan_matcher,
                    constraint);
});
// constraint_task 依赖 scan_matcher_task
constraint_task->AddDependency(scan_matcher->creation_task_handle);
auto constraint_task_handle =
    thread_pool_->Schedule(std::move(constraint_task));
// finish_node_task_ 依赖 constraint_task
finish_node_task_->AddDependency(constraint_task_handle);

其实MaybeAddConstraint做的就是下面的工作，接下来的重点就是 ConstraintBuilder2D::ComputeConstraint

二叉树|数学基础

四叉树和八叉树就是2D和3D的“二分法”，搜索过程与二叉树搜索也类似，二叉树中是将数组sort后存入二叉树中，从而在查找中实现时间复杂度为log2N；四叉树/八叉树是按平面/空间范围划分有序node，将所有points（坐标已知，但是每个点的point在vector中的index可以认为是随机的，没有规律的，所以不能直接根据index取出point(x,y)）放入所属node中，实现所有points的sorted，进而在搜索时，实现时间复杂度为logN

后端 3 ComputeConstraintsForNode|激光SLAMCartographer源码解读
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct Constraint
{
    struct Pose
    {
      transform::Rigid3d   zbar_ij;
      double translation_weight;
      double rotation_weight;
    };
    SubmapId submap_id;  // 'i' in the paper.
    NodeId node_id;      // 'j' in the paper.
    // Pose of the node 'j' relative to submap 'i'.
    Pose pose;
    // Differentiates between intra-submap (where node 'j' was inserted into
    // submap 'i') and inter-submap constraints (where node 'j' was not 
    // inserted  into submap 'i').
    enum Tag { INTRA_SUBMAP, INTER_SUBMAP } tag;
};

现在看PoseGraph2D::AddNode最后的计算约束

1
2
3
4
5
6
7
8
WorkItem::Result PoseGraph2D::ComputeConstraintsForNode(
    const NodeId& node_id,
    std::vector<std::shared_ptr<const Submap2D>> insertion_submaps,
    const bool newly_finished_submap)
{
  std::vector<SubmapId> submap_ids;
  std::vector<SubmapId> finished_submap_ids;
  std::set<NodeId> newly_finished_submap_node_ids;

下面的内容都放到一个大括号内了

1
2
3
4
5
6
7
{
  absl::MutexLock locker(&mutex_);
  const auto& constant_data =
      data_.trajectory_nodes.at(node_id).constant_data;
  //如果只有1个子图，则返回index为0，否则返回最新的两个连续的submap id
  submap_ids = InitializeGlobalSubmapPoses(
      node_id.trajectory_id, constant_data->time, insertion_submaps);

这里有重要函数InitializeGlobalSubmapPoses

InitializeGlobalSubmapPoses

这个主要是为了计算论文里的 $\xii^m$，最终返回的是子图 Id

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
std::vector<SubmapId> PoseGraph2D::InitializeGlobalSubmapPoses(
    const int trajectory_id, const common::Time time,
    const std::vector<std::shared_ptr<const Submap2D>>& insertion_submaps)
{
  CHECK(!insertion_submaps.empty());
  // std::unique_ptr<optimization::OptimizationProblem2D>  optimization_problem_;
  // MapById<SubmapId, SubmapSpec2D>   submap_data
  const auto& submap_data = optimization_problem_->submap_data();
  // insertion_submaps 只有一个子图的情况
  // 说明这是该trajectory的第一张 submap
  if (insertion_submaps.size() == 1)
  {
    // If we don't already have an entry for the first submap, add one.
    if (submap_data.SizeOfTrajectoryOrZero(trajectory_id) == 0)
    {
      if (data_.initial_trajectory_poses.count(trajectory_id) > 0)
      {
        data_.trajectory_connectivity_state.Connect(
            trajectory_id,
            data_.initial_trajectory_poses.at(trajectory_id).to_trajectory_id,
            time);
      }
      // 计算该submap的global_pose(查找轨迹的初始位姿来计算), 后加入优化问题
      // ComputeLocalToGlobalTransform 是 local to global map frame transform
      optimization_problem_->AddSubmap(
          trajectory_id, transform::Project2D(
          ComputeLocalToGlobalTransform(
          data_.global_submap_poses_2d, trajectory_id) *
            insertion_submaps[0]->local_pose()
               )
          );
    }
    CHECK_EQ(1, submap_data.SizeOfTrajectoryOrZero(trajectory_id));
    // 该trajectory的第一张 submap， 索引 0
    const SubmapId submap_id{trajectory_id, 0};
    CHECK(data_.submap_data.at(submap_id).submap == insertion_submaps.front());
    return {submap_id};
  }
  // 前端维护两个子图了
  CHECK_EQ(2, insertion_submaps.size());
  const auto end_it = submap_data.EndOfTrajectory(trajectory_id);
  CHECK(submap_data.BeginOfTrajectory(trajectory_id) != end_it);
  const SubmapId  last_submap_id  =  std::prev(end_it)->id;
   // submap 是 InternalSubmapData类型的成员
  if (data_.submap_data.at(last_submap_id).submap ==
      insertion_submaps.front()  )
  {
    // 此时，'last_submap_id' is the ID of 'insertions_submaps.front()'
    // 'insertions_submaps.back()' is new，也就是没插入

    // 如果有2个子图，把第1个子图的 global_pose 加入优化问题
    // 计算第一张子图的 global_pose，last_submap_id已经在后端里
    const auto& first_submap_pose = submap_data.at(last_submap_id).global_pose;
    // ComputeSubmapPose函数  其实就是 submap.local_pose()
    optimization_problem_->AddSubmap(
        trajectory_id,
        first_submap_pose *
            constraints::ComputeSubmapPose(*insertion_submaps[0]).inverse() *
            constraints::ComputeSubmapPose(*insertion_submaps[1])  );
    return { last_submap_id,  
            SubmapId{trajectory_id, last_submap_id.submap_index + 1}  };
  }
  // 不是上面两种情况，也就是已经加入了 back()
  CHECK(data_.submap_data.at(last_submap_id).submap ==
        insertion_submaps.back() );
  const SubmapId front_submap_id{trajectory_id,
                                 last_submap_id.submap_index - 1};
  CHECK(data_.submap_data.at(front_submap_id).submap ==
        insertion_submaps.front());
  // 如果不是上面两种情况，那就返回目前最后的两个子图，front_submap_id是更旧的子图
  return {front_submap_id, last_submap_id};
}

这里之所以出现三种情况，是之前的AppendNode中的`data.submap_data.Append`插入子图。

第1种情况用到的ComputeLocalToGlobalTransform在前面讲过。

第2种情况的公式实际是 ， 也就是 ，把现有的local to global map的变换用作新子图的位姿计算。

第3种很简单，相当于没处理全局位姿。

计算 INTRA_SUBMAP

返回继续看 ComputeConstraintsForNode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
CHECK_EQ(submap_ids.size(), insertion_submaps.size());
const SubmapId matching_id = submap_ids.front();
// node(scan) 在 local map坐标系的位姿
const transform::Rigid2d   local_pose_2d =
    transform::Project2D(constant_data->local_pose *
                         transform::Rigid3d::Rotation(
                             constant_data->gravity_alignment.inverse() ) );
// 全局位姿，通过优化后的 submap全局位姿和 local位姿求出矩阵
// ComputeSubmapPose返回 参数子图的 local_pose
const transform::Rigid2d global_pose_2d =
    optimization_problem_->submap_data().at(matching_id).global_pose *
    constraints::ComputeSubmapPose(*insertion_submaps.front()).inverse() *
    local_pose_2d;
 // 优化器中增加轨迹节点信息
optimization_problem_->AddTrajectoryNode(
    matching_id.trajectory_id,
    optimization::NodeSpec2D{constant_data->time, local_pose_2d,
                             global_pose_2d,
                             constant_data->gravity_alignment}  );

for (size_t i = 0; i < insertion_submaps.size(); ++i)
{
  const SubmapId  submap_id = submap_ids[i];
  // Even if this was the last node added to 'submap_id', the submap will
  // only be marked as finished in 'data_.submap_data' further below.
  CHECK( data_.submap_data.at(submap_id).state ==
        SubmapState::kNoConstraintSearch );
  data_.submap_data.at(submap_id).node_ids.emplace(node_id);
  // node_id的 scan pose 在子图中的 相对位置，就是后面的 intra constrait
  const transform::Rigid2d   constraint_transform =
    constraints::ComputeSubmapPose(*insertion_submaps[i]).inverse() *
      local_pose_2d;
  /*  遍历matching结果的所有submap，其新增加的轨迹节点必定组成了其submap，
  故其约束为 INTRA_SUBMAP 类型约束，可直接将相对位置加入约束队列中  */
  data_.constraints.push_back(
      Constraint{ submap_id, node_id,
                { transform::Embed3D(constraint_transform),
                  options_.matcher_translation_weight(),
                  options_.matcher_rotation_weight()},
                 Constraint::INTRA_SUBMAP}   );
}

这里是计算 intra 约束的地方。

匹配的过程就是建立约束的过程，也就是回环检测的过程，因为Cartographer 采用的是图优化，有节点和约束的概念，，节点可以理解为激光点的位姿，约束就是激光数据与子图之间相对位姿。

一共建立3种约束：

  • 匹配结果的所有子图，必定包含了新增加的轨迹节点，它们的约束是 INTRA_SUBMAP
  • 新增的节点和已经完成约束计算的子图都要计算约束
  • 对于新的子图不再添加新的轨迹节点时，建立其他节点和该子图之间的约束

后两个就是下面的两次ComputeConstraint函数，是INTER约束

子图在后台线程有两种状态 kNoConstraintSearch 和 kFinished。对于前者的子图，只有内部node去匹配；对后者的子图，所有node(包括新node)都匹配这个子图

两次 ComputeConstraint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
for (const auto& submap_id_data : data_.submap_data)
{
  // 完成过约束计算的子图
  if (submap_id_data.data.state == SubmapState::kFinished)
  {
    // 不包含当前的节点  node_id
    CHECK_EQ(submap_id_data.data.node_ids.count(node_id), 0);
    finished_submap_ids.emplace_back(submap_id_data.id);
  }
}
// 前端匹配输出的submap是刚完成的一个，即维护的两个submap中front不再更新
if (newly_finished_submap)
{
  const SubmapId  newly_finished_submap_id = submap_ids.front();
  InternalSubmapData&   finished_submap_data =
      data_.submap_data.at(newly_finished_submap_id);
  CHECK(finished_submap_data.state == SubmapState::kNoConstraintSearch);
  // 将新的submap设置为finished，表明已经增加约束条件了
  finished_submap_data.state = SubmapState::kFinished;
  newly_finished_submap_node_ids = finished_submap_data.node_ids;
}
}

要遍历的submap_data 是 MapById<SubmapId, InternalSubmapData>，该容器记录了所有的子图数据及其内部节点，InternalSubmapData除了描述了子图的数据之外还记录了所有内部的节点，成员是

1
2
3
4
5
6
7
8
// enum class SubmapState { kActive, kFinished };    
struct InternalSubmapData
{
    std::shared_ptr<const Submap2D> submap;
    // 所有直接插入submap的节点
    std::set<NodeId> node_ids;
    SubmapState state = SubmapState::kActive;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  // 新加入的节点与之前所有完成约束计算的子图，均计算一次约束
for (const auto& submap_id : finished_submap_ids)
    ComputeConstraint(node_id, submap_id);
  /* 每次新的子图完成，不再更新即不再添加新的轨迹节点时，
  则需要计算此子图与所有优化位姿图node之间的约束 */
if (newly_finished_submap)
{
    const SubmapId newly_finished_submap_id = submap_ids.front();
    // We have a new completed submap, so we look into 
    // adding constraints for  old nodes
    for (const auto& node_id_data : optimization_problem_->node_data() )
    {
      const NodeId&  node_id = node_id_data.id;
      if (newly_finished_submap_node_ids.count(node_id) == 0)
      {
        ComputeConstraint(node_id, newly_finished_submap_id);
      }
    }
}

子图的状态主要是给后台的线程提供的。一开始子图的状态都是kActive的，当它完成之后(kFinished的状态)就会与所有旧的节点 计算约束

此外新增的节点也会与所有完成的子图 计算约束。这一次可以理解为是进行回环检测，根据节点和循环中的各个子图之间的情况不同，可能构建的是全局约束，也可能是局部约束。 回环检测是一种全局约束。

PoseGraph2D::ComputeConstraint只有这里的两次调用。

最后部分

1
2
3
4
5
6
7
8
9
10
11
12
13
  // 每次新添加一个节点时，均需执行，通知约束构建器。
  constraint_builder_.NotifyEndOfNode();
  absl::MutexLock locker(&mutex_);
  // 记录距离上次闭环处理增加的节点个数
  ++num_nodes_since_last_loop_closure_;
  // 当新增加节点个数大于阈值时，则调用优化处理结果
  if (options_.optimize_every_n_nodes() > 0 &&
      num_nodes_since_last_loop_closure_ > options_.optimize_every_n_nodes())
  {
    return WorkItem::Result::kRunOptimization;
  }
  return WorkItem::Result::kDoNotRunOptimization;
}

添加节点和约束是实时的，但是优化不是，更不需要每个节点都进行。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void ConstraintBuilder2D::NotifyEndOfNode()
{
  absl::MutexLock locker(&mutex_);
  CHECK(finish_node_task_ != nullptr);
  // 完成一个后端节点
  finish_node_task_->SetWorkItem([this] {
    absl::MutexLock locker(&mutex_);
    ++num_finished_nodes_;
  });
  auto finish_node_task_handle =
      thread_pool_->Schedule(std::move(finish_node_task_));
  // 重新开始添加节点任务
  finish_node_task_ = absl::make_unique<common::Task>();
  when_done_task_->AddDependency(finish_node_task_handle);
  ++num_started_nodes_;
}

这里就是处理finish_node_task_，每次完成一个node约束计算时均会进行调用。目的是完成finish_node_task_，同时开启一个新的task用于下一次约束任务。

后端 7 分支定界|激光SLAMCartographer源码解读

算法思想

在Local SLAM中，通过在子图中的Scan-to-map匹配过程可以得到了一个比较理想的机器人位姿估计。 但由于Local SLAM只使用了一段时间内的局部信息，所以定位误差还会随着时间累积。为了能够进一步的降低局部误差累积的影响，Cartographer还需要通过Pixel-accurate扫描匹配来进行闭环检测， 进一步的优化机器人的位姿估计。 分支定界时，地图一定要完整

记 为雷达扫描到的 个hit点集合， 是第k个hit点在scan frame下的坐标，在地图坐标系下的坐标表示为

其中 ，用表示位姿估计描述的坐标变换。

Pixel-accurate扫描匹配问题可以用下式来描述:

其中 是一个搜索窗口， 是离最近的栅格单元的占用概率。也就是在搜索窗口中找到一个最优的位姿，使得hit点集合出现的概率最大化。


这里和前端的实时相关性匹配有部分相似，但是多分辨率地图和分支定界是新加入的。机器人的位姿是用表示，对于暴力匹配法来说，该方法的搜索步长为1，搜索窗口的栅格索引集合 可以通过笛卡尔积枚举：

其中 和 是x 和 y方向上的最大搜索索引，是搜索角度的最大索引。搜索窗口就可以用集合 表示。 是搜索中心，也是机器人位姿的初始估计， 和 分别是位移和角度的搜索步长。

如果直接用暴力搜索就太复杂了，所以使用深度优先的分支定界法。使用一个满四叉树的概念，这跟二叉树是类似的。

其根节点代表整个搜索窗口 。树中的每一个节点的孩子都是对该节点所代表的搜索空间的一个划分， 每个叶子节点都对应着一个解。

树共有8层，分别表示从顶层（）到底层/叶子（），树的深度depth每增加1，搜索步长step就减半，表示查找的分辨率越高。每次对x和y都减半操作，像分田一样。如果栅格地图分辨率是0.05m（一个栅格的物理长度），step与depth的关系如下：


比如在树的最底层，， 此时 且 ，显然只有1个解。

对于一个candidate，可构建四个子Candidate。C层搜索空间：

搜索树上的每个节点的上界可以通过下式计算得到：

Cartographer仍然采取了一种空间换时间的方法来进一步的提高搜索效率。预算图（precomputed grids）又叫膨胀图，从上面我们知道了树的每一层都对应一个步长，根据这个步长，生成一个对应的膨胀图。步长越大，膨胀级别越高。 根节点的分辨率是最粗的。Cartographer还为每个子图预先计算了不同尺度下的占用概率，以后的搜索过程只需要简单的查表就可以完成了。

需要注意的是膨胀不会改变栅格图的分辨率，改变的仅仅是栅格图中像素值而已。这个膨胀的过程比较复杂，源码里是用一种滑动窗口的机制实现的。

整个搜索过程借助了一个栈{C}来完成，首先将整个搜索空间分割，得到初始的子空间节点集合 。 然后对集合 中的节点根据它们的上界进行排序，并依次入栈{C}保证得分最高的节点在栈顶的位置。这样可以优先搜索最有可能的解空间。



最底层的节点是所有候选的评分， 这是以两个叶子节点做示范。 父节点的贪心得分永远大于子节点的贪心得分。从而保证，一旦父节点的贪心得分小于best_score，那么这个父节点的子树全部被剪枝，因为其子树的叶子节点的得分肯定也小于best_score。

源码

接上一篇的分支定界部分

1
2
3
4
5
const Candidate2D best_candidate = BranchAndBound(
    discrete_scans,   search_parameters, 
    lowest_resolution_candidates,
    precomputation_grid_stack_->max_depth(), 
    min_score);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// 初始传入的candidates为最上层的候选解
// 初始 candidate_depth = 7
// min_score 在lua里设置
Candidate2D FastCorrelativeScanMatcher2D::BranchAndBound(
    const std::vector<DiscreteScan2D>&  discrete_scans,
    const SearchParameters&  search_parameters,
    const std::vector<Candidate2D>&  candidates,
    const int  candidate_depth,
    float  min_score) const
{
  // 检查是否是最底层(叶子层)，如果已经查找到最底层了，则返回分数最高的候选解
  if (candidate_depth == 0)
      return *candidates.begin();
  // Candidate2D的构造
  // 参数分别为：0：scan_index，即旋转序号
  // 0：x方向的偏移序号  0：y方向的偏移数   search_parameters：搜索参数
  Candidate2D best_high_resolution_candidate(0, 0, 0, search_parameters);
  
  best_high_resolution_candidate.score = min_score;
  // 对传入的候选人candidate进行循环，即从最上层开始遍历
  for (const Candidate2D& candidate : candidates)
  {
    // 将叶子节点与某棵分枝树的非叶子节点进行比较，如果非叶子节点的分数小于
    // 之前选出的最高分叶子节点，则直接将此非叶子节点candidate及其子树全部砍掉
    if(candidate.score <= min_score)
        break;

    // 一个容器，盛放这个节点引出的四个下一层的候选者
    std::vector<Candidate2D> higher_resolution_candidates;
    
    // 区域边长右移，相当于步长减半，进行分枝
    const int half_width = 1 << (candidate_depth - 1);
    
    // 对x、y偏移进行遍历，求出这一个candidate的四个子节点候选人（即最上面遍历的那个元素）
    for (int x_offset : {0, half_width}  )
    {  // 只能取0和half_width
      if (candidate.x_index_offset + x_offset >
          search_parameters.linear_bounds[candidate.scan_index].max_x)
           // 超出边界则break
           break;
      for (int y_offset : {0, half_width}  )
      {  // 只能取0和half_width   xy一共遍历四个子节点
        if (candidate.y_index_offset + y_offset >
            search_parameters.linear_bounds[candidate.scan_index].max_y)
            // 超出边界则break
            break;

        // 候选者依次推进来，一共4个
        // 可以看出，分枝定界方法的分枝是向右下角的四个子节点进行分枝
        higher_resolution_candidates.emplace_back(
            candidate.scan_index, candidate.x_index_offset + x_offset,
            candidate.y_index_offset + y_offset, search_parameters);
      }
    }
    // 对candidate四个子节点进行打分，并将
    // higher_resolution_candidates 按照score从大到小的顺序进行排列
    ScoreCandidates(precomputation_grid_stack_->Get(candidate_depth - 1),
                    discrete_scans, search_parameters,
                    &higher_resolution_candidates);
    // 开始递归
    best_high_resolution_candidate = std::max(
        best_high_resolution_candidate,
        BranchAndBound(discrete_scans, search_parameters,
                       higher_resolution_candidates, candidate_depth - 1,
                       best_high_resolution_candidate.score));
  }
  return best_high_resolution_candidate;
}

第一步应先求取顶层的解及其对应评分（即可能位置和对应匹配置信度）。每层的当前节点的对应的评分均大于等于其所有下层枝叶节点，即上边界。由于不同分辨率地图存储格式，显然满足上边界条件。低分辨地图下的匹配置信度显然高于下层的高分辨地图下的匹配，然后采用迭代方法裁剪枝叶，直到遍历所有叶子节点。

在地图预处理时，其分辨率按照2的层数次方进行压缩的，由于地图有x和y两个方向，因此此层的一个节点，在下层会分为4个节点，即分辨率会放大2倍

参考：分枝定界图解

后端 6 快速相关性匹配|激光SLAMCartographer源码解读

如果当前的scan和所有已创建完成的submap中的某个scan的位姿在距离上足够近，那么通过某种 scan match策略就会找到该闭环。Fast Correlative scan match 就是回环检测

FastCorrelativeScanMatcher2D的构造函数

1
2
3
4
5
6
7
FastCorrelativeScanMatcher2D::FastCorrelativeScanMatcher2D(
    const Grid2D& grid,
    const proto::FastCorrelativeScanMatcherOptions2D& options)
    : options_(options),
      limits_(grid.limits()),
      precomputation_grid_stack_(
    absl::make_unique<PrecomputationGridStack2D>(grid, options) ) {}

再来看PrecomputationGridStack2D的构造函数，引入预算图的概念(precomputed grids)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 存储同一个地图但分辨率不同，低分辨率地图value，采用对应高分辨地图中子格中最高分辨率
PrecomputationGridStack2D::PrecomputationGridStack2D(
    const Grid2D& grid,
    const proto::FastCorrelativeScanMatcherOptions2D& options)
{
  CHECK_GE(options.branch_and_bound_depth(), 1);
  // 确定最粗的分辨率，也就是64个栅格合成一个格子
  // 注意不是7次方，而是2的6次方，64
  const int max_width = 1 << (options.branch_and_bound_depth() - 1);

  // vector<PrecomputationGrid2D>  precomputation_grids_;
  precomputation_grids_.reserve(options.branch_and_bound_depth());
  std::vector<float> reusable_intermediate_grid;
  const CellLimits limits = grid.limits().cell_limits();
  // vector 大小为，应该是每层存储的的grid，空间开辟意义不大，每层都会再次resize
  reusable_intermediate_grid.reserve((limits.num_x_cells + max_width - 1) *
                                     limits.num_y_cells);
  for (int i = 0; i != options.branch_and_bound_depth(); ++i)
  {
    /*  precomputation_grids_插入的仍然是7个
    从 2^0(0.05)  到  2^6
    队列中最前的为分辨率最高的地图，需要对原图进行扩展，而width是扩展和偏移量
    emplace_back会生成一个临时的变量，会调用PrecomputationGrid2D的构造函数
     */
    const int width = 1 << i;
    precomputation_grids_.emplace_back(grid, limits, width,
                          &reusable_intermediate_grid);
  }
}

传入地图grid为原分辨率地图，即为最高分辨地图。预处理地图堆栈则保存了n张不同分辨率的栅格地图，存储压缩2,4,8,16倍等等地图。首先是原分辨率地图，最后存储最粗分辨率的地图。不同层的地图，目的是后续相关匹配在不同分辨率地图下匹配，即为分支定界中的层。为保证上边界正确性，高层中的评分一定高于其底层节点的评分。压缩的地图并非直接从原图固定间隔采样，而是将固定间隔中所有坐标概率值最大值作为低分辨率地图，以此类推完成整个地图栈预处理。

在低分率下的地图匹配其相关性一定较高，如果分辨率继续降低，则极限为概率为1。

原始地图一直是不变的，例如每一层的分辨率都是在原始地图上生成的。即4 * origin_resolution分辨率地图是在origin_resolution分辨率地图上生成，而不是在2 * origin_resolution分辨率地图上生成的.

Match函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
input:
当前帧估计位置（里程计等提供的初始位置）
当前帧点云（即以激光雷达为坐标系的点云）
最小置信度
（grid在构造函数已经传递）

output：
置信度清单
匹配后输出位置
 */
bool FastCorrelativeScanMatcher2D::Match(
    const transform::Rigid2d& initial_pose_estimate,
    const sensor::PointCloud& point_cloud, const float min_score, float* score,
    transform::Rigid2d* pose_estimate) const
{
	// 还是前端的相关性匹配那个搜索参数
  const SearchParameters search_parameters(options_.linear_search_window(),
                                           options_.angular_search_window(),
                                           point_cloud, limits_.resolution());
  return MatchWithSearchParameters(search_parameters, initial_pose_estimate,
                                   point_cloud, min_score, score,
                                   pose_estimate);
}

MatchWithSearchParameters

开始部分同前端的相关性匹配相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool FastCorrelativeScanMatcher2D::MatchWithSearchParameters(
    SearchParameters search_parameters,
    const transform::Rigid2d& initial_pose_estimate,
    const sensor::PointCloud& point_cloud, float min_score, float* score,
    transform::Rigid2d* pose_estimate) const
{
  CHECK(score != nullptr);
  CHECK(pose_estimate != nullptr);
   
  const Eigen::Rotation2Dd initial_rotation = initial_pose_estimate.rotation();
  // 将点云旋转至初始位置（即估计位置）航向方向上
  const sensor::PointCloud rotated_point_cloud = sensor::TransformPointCloud(
      point_cloud,
      transform::Rigid3f::Rotation(Eigen::AngleAxisf(
          initial_rotation.cast<float>().angle(), Eigen::Vector3f::UnitZ())));
  // 根据将角度窗口按照一定分辨率划分，并根据每一个旋转角度将点云旋转，生成N个点云
  const std::vector<sensor::PointCloud> rotated_scans =
      GenerateRotatedScans(rotated_point_cloud, search_parameters);
  
  // 将所有点云转换到初始位置上
  const std::vector<DiscreteScan2D> discrete_scans = DiscretizeScans(
      limits_, rotated_scans,
      Eigen::Translation2f(initial_pose_estimate.translation().x(),
                           initial_pose_estimate.translation().y()));



中间部分其实还是和前端那里类似

1
2
3
4
5
// 修复下所有点云的大小在空间的大小，即边界
search_parameters.ShrinkToFit(discrete_scans, limits_.cell_limits());
//获取低分辨率的量化列表（和标准相关方法对比），并且计算匹配评分结果，并进行了排序
const std::vector<Candidate2D> lowest_resolution_candidates =
    ComputeLowestResolutionCandidates(discrete_scans, search_parameters);
1
2
3
4
5
6
7
8
9
10
11
12
std::vector<Candidate2D>
FastCorrelativeScanMatcher2D::ComputeLowestResolutionCandidates(
    const std::vector<DiscreteScan2D>& discrete_scans,
    const SearchParameters& search_parameters) const
{
  std::vector<Candidate2D> lowest_resolution_candidates =
      GenerateLowestResolutionCandidates(search_parameters);
  ScoreCandidates(
      precomputation_grid_stack_->Get(precomputation_grid_stack_->max_depth()),
      discrete_scans, search_parameters, &lowest_resolution_candidates);
  return lowest_resolution_candidates;
}

GenerateLowestResolutionCandidates生成候选的最粗分辨率像素偏移集,，要注意的是

1
2
3
4
5
6
7
// 注意不是7次方，而是2的6次方，64
const int linear_step_size = 1 << precomputation_grid_stack_->max_depth();
			......
const int num_lowest_resolution_linear_x_candidates =
        (search_parameters.linear_bounds[scan_index].max_x -
         search_parameters.linear_bounds[scan_index].min_x + linear_step_size) /
        linear_step_size;

这里和前端的处理稍微不同，是为了处理最低分辨率的地图，搜索空间也与最低分辨率一致，最后所有位置及其对应评分放入集合中。

ScoreCandidates函数计算评分，并按照评分从高到低排序，最后返回分数从大到小排列的像素偏移集.

剩下的就是分支定界，然后把最佳候选的得分和最小得分比较，获得位姿

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 分支边界搜索最佳匹配
const Candidate2D best_candidate = BranchAndBound(
      discrete_scans,   search_parameters, 
      lowest_resolution_candidates,
      precomputation_grid_stack_->max_depth(), 
      min_score);

if (best_candidate.score > min_score)
{
    *score = best_candidate.score;
    *pose_estimate = transform::Rigid2d(
        {initial_pose_estimate.translation().x() + best_candidate.x,
         initial_pose_estimate.translation().y() + best_candidate.y},
        initial_rotation * Eigen::Rotation2Dd(best_candidate.orientation));
    return true;
}
  return false;
}

降低CPU占用的配置|激光SLAMCartographer原理和配置
abstract Welcome to my blog, enter password to read.
Read more
后端 2 AppendNode|激光SLAMCartographer源码解读

后端优化问题也是一个非线性最小二乘问题，用ceres解决。

$arg\ \mathop{min}\limits{\Xi^m \ \Xi^s} \frac{1}{2}\sum \limits{ij} \rho(E^2(\xii^2, \xi_j^2; \Sigma{ij}, \xi_{ij})\ ) \tag1$

全局地图是由很多个子图拼接而成的，那么每一个子图在世界坐标系下都有一个位姿，它们的位姿可以用下面的集合表示
$\Xi^m = \left{\xii^m\right}{i=1,2…m}$

前端每完成一次子图更新，会把一帧激光扫描数据插入其维护的子图当中。这个插入结果将被Cartographer看做是构成一条轨迹的节点，并以此时的机器人位姿作为节点的位姿，将其看做是一次激光扫描的参考位姿，所有位姿的集合如下表示
$\Xi^s = \left{\xij^s\right}{j=1,2…n}$

这些被优化的submap位姿和Scan位姿构成了一些constraint（约束）。constraint的表现形式就是位姿 $\xi{ij}$ 和协方差矩阵 $\Sigma{ij}$。 位姿 $\xi_{ij}$ 代表 j 帧Scan在子图 i 下的位姿，描述scan和哪个submap匹配

(1)式中的残差E计算公式是

损失函数ρ（例如Huber损失），可以用于减少异常值的影响，而 异常值可能会出现在局部对称的环境（包含隔间的办公室）中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
NodeId PoseGraph2D::AppendNode(
    std::shared_ptr<const TrajectoryNode::Data> constant_data,
    const int trajectory_id,
    const std::vector<std::shared_ptr<const Submap2D>>& insertion_submaps,
    const transform::Rigid3d&  optimized_pose )
{
  absl::MutexLock locker(&mutex_);
  // 判断对轨迹进行的操作，包括增加，删除或者轨迹之间的关系操作
  // 仍然假设仅有一个轨迹
  AddTrajectoryIfNeeded(trajectory_id);
  // 此 trajectory id 的轨迹是否存在或更改，只是判断
  if (!CanAddWorkItemModifying(trajectory_id))
  {
      LOG(WARNING) << "AddNode was called for finished or deleted trajectory";
  }

这些对于一条轨迹的情况都不重要，先不深入分析

1
2
3
4
5
// 添加scan的node_id，返回 trajectory id 和对应的 scan idex
const NodeId node_id = data_.trajectory_nodes.Append(
    trajectory_id, TrajectoryNode{constant_data, optimized_pose} );
// 记录轨迹节点个数  +1
++data_.num_trajectory_nodes;

data_ 是 PoseGraphData data_ GUARDED_BY(mutex_);

trajectory_nodes的类型是MapById<NodeId, TrajectoryNode>，对于Append函数，不必关心细节。里面的TrajectoryNode类型是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct TrajectoryNode
{
  // 记录了前端传来的 点云、重力方向、局部位姿等数据
  struct Data {
    // 扫描数据被插入子图的时刻
    common::Time time;
    // Transform to approximately gravity align the tracking frame as
    // determined by local SLAM.
    Eigen::Quaterniond gravity_alignment;
    // Used for loop closure in 2D: voxel filtered returns in the
    // 'gravity_alignment' frame.
    sensor::PointCloud filtered_gravity_aligned_point_cloud;
    // 省略用于3D建图时闭环检测的字段

    // The node pose in the local SLAM frame.
    transform::Rigid3d  local_pose;
  };
  common::Time time() const { return constant_data->time; }
  // 实际只有这两个成员
  std::shared_ptr<const Data>  constant_data;
  // The node pose in the global SLAM frame.
  transform::Rigid3d  global_pose;

最重要的是global_pose，节点在世界坐标系下的位姿，论文里的
返回去查，发现是GetLocalToGlobalTransform返回的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// Test if the 'insertion_submap.back()' is one we never saw before.
// 前端最新的子图与当前 data_ 最后一个子图不一致时，才会增加
if ( data_.submap_data.SizeOfTrajectoryOrZero(trajectory_id) == 0 ||
      std::prev(data_.submap_data.EndOfTrajectory(trajectory_id)  )
              ->data.submap != insertion_submaps.back()  )
{
    // 在全局数据data_中添加submap信息，添加时只考虑新增加的submap
    // InternalSubmapData() 在这里的意思是无参的构造函数，什么都未处理
    const SubmapId   submap_id = 
          data_.submap_data.Append(trajectory_id, InternalSubmapData()  );
    // 闭环中submap节点，采用最新的子图
    // submap_data 是 MapById<SubmapId, InternalSubmapData>
    // 成员submap是个智能指针
    data_.submap_data.at(submap_id).submap = insertion_submaps.back();
    LOG(INFO) << "Inserted submap " << submap_id << ".";
    kActiveSubmapsMetric->Increment();
}
    return node_id;
}

增加了该节点在 global map坐标系的全局位姿，也是后期需要优化的位姿。把node加入到trajectory_nodes列表。 最后返回的位姿图ID为data_存储的轨迹节点ID。

前端最新的子图与当前 data_ 最后一个子图不一致时，给该子图分配id并将其加入其中(其实就是把前端最新子图加入到后端)。注意，这时候的子图 还没有计算global pose，也就是 。 所以，后面要初始化submap的global pose，也就是InitializeGlobalSubmapPoses

处理子图 4. 结束子图|激光SLAMCartographer源码解读

void Submap2D::Finish()

1
2
3
4
CHECK(grid_);
CHECK(!insertion_finished());
grid_ = grid_->ComputeCroppedGrid();
set_insertion_finished(true);

这里的set_insertion_finished(true);就是子图结束建图了，可以添加函数isFinished判断，其实就是判断insertion_finished_是否true。 子图建完才会进入后端

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
std::unique_ptr<Grid2D> ProbabilityGrid::ComputeCroppedGrid() const
{
  Eigen::Array2i offset;
  CellLimits cell_limits;
  ComputeCroppedLimits(&offset, &cell_limits);
  const double resolution = limits().resolution();
  const Eigen::Vector2d max =
      limits().max() - resolution * Eigen::Vector2d(offset.y(), offset.x());
      // conversion_tables_ 是两个表
  std::unique_ptr<ProbabilityGrid> cropped_grid =
      absl::make_unique<ProbabilityGrid>(
          MapLimits(resolution, max, cell_limits), conversion_tables_);
   // 对应的cell设置概率，在SetProbability里又转成了空闲概率
  for (const Eigen::Array2i& xy_index : XYIndexRangeIterator(cell_limits))
  {
    if (!IsKnown(xy_index + offset)) continue;
    cropped_grid->SetProbability(xy_index, GetProbability(xy_index + offset) );
  }
  return std::unique_ptr<Grid2D>(cropped_grid.release());
}
1
2
3
4
void set_insertion_finished(bool insertion_finished)
{
    insertion_finished_ = insertion_finished;
}
处理子图 3. CastRays和更新栅格概率|激光SLAMCartographer源码解读

  • ros的地图坐标系: 左下角为原点, 向右为x正方向, 向上为y正方向, 角度以x轴正向为0度, 逆时针为正

  • cartographer的地图坐标系: 坐标系右下角为原点, 向上为x正方向, 向左为y正方向角度正方向以x轴正向为0度, 逆时针为正。左上角为坐标的最大值

  • cartographer的像素坐标系: 左上角为原点, 向右为x正方向, 向下为y正方向

Cartographer中，Eigen::Array2i指像素坐标， Eigen::Vector2f指地图坐标.

在函数MapLimits::GetCellIndex和GetCellCenter可以看到cartographer的地图坐标系和像素坐标系的转换

MapLimits的几个重要成员函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 计算物理坐标点的像素索引
// 返回的这个点是栅格的中心点，因此，栅格点(grid_point)是一个格子的中心
Eigen::Array2i GetCellIndex(const Eigen::Vector2f& point) const
{
  // Index values are row major and the top left has Eigen::Array2i::Zero()
  // and contains (centered_max_x, centered_max_y). We need to flip and
  // rotate.
  return Eigen::Array2i(
      common::RoundToInt((max_.y() - point.y()) / resolution_ - 0.5),
      common::RoundToInt((max_.x() - point.x()) / resolution_ - 0.5));
}

// 根据像素索引计算物理坐标
Eigen::Vector2f GetCellCenter(const Eigen::Array2i cell_index) const
{
  return {max_.x() - resolution() * (cell_index[1] + 0.5),
          max_.y() - resolution() * (cell_index[0] + 0.5)};
}
// 判断像素索引是否在栅格地图内
bool Contains(const Eigen::Array2i& cell_index) const
{
  return (Eigen::Array2i(0, 0) <= cell_index).all() &&
         (cell_index <
          Eigen::Array2i(cell_limits_.num_x_cells, cell_limits_.num_y_cells))
             .all();
}

Insert函数

1
2
3
4
5
6
7
8
9
10
11
void ProbabilityGridRangeDataInserter2D::Insert(
    const sensor::RangeData& range_data, GridInterface* const grid) const 
{
    ProbabilityGrid* const  probability_grid = static_cast<ProbabilityGrid*>(grid);
    CHECK(probability_grid != nullptr);
    // By not finishing the update after hits are inserted, we give hits priority
    // (i.e. no hits will be ignored because of a miss in the same cell).
    CastRays(range_data,  hit_table_,  miss_table_,  
             options_.insert_free_space(), probability_grid);
    probability_grid->FinishUpdate();
}

输入的range_data在LocalTrajectoryBuilder2D::AddRangeData的最后部分，已经计算了misses和returns(注意不是 hit) 先看传感器数据类型RangeData的定义：

1
2
3
4
5
6
7
8
9
struct RangeData {
	Eigen::Vector3f   origin;    // 当次扫描测量时激光雷达的位置
	// PointCloud就是 vector<Eigen::Vector3f>
	// 扫描到的hit点与miss点
	PointCloud   returns;
	PointCloud   misses;
};
// 对 2D SLAM， 第三个元素为0
// typedef std::vector<Eigen::Vector3f> PointCloud;

所谓的hit点是指在该点上扫描到了障碍物，该点所在的栅格单元就发生了一次hit事件。miss点所在的位置上并没有检测到障碍物，只是以传感器的最远有效距离记录下坐标而已。

之前获得的带有时间戳的点云类型TimedPointCloud并没有区分hit点和miss点 ，该数据类型只是将原始数据中的距离和扫描角度信息转换为空间点的坐标。


看到这里，参数grid的来源已经记不清了，往回查会发现，它的根源是ActiveSubmaps2D::AddSubmap的添加子图里，也就是Submap2D的构造函数，最终是CreateGrid函数

CastRays

从扫描得到的距离信息转换为栅格的hit或者miss事件的过程称为RayCasting，函数原型

1
2
3
4
void CastRays(const sensor::RangeData& range_data,
	  const std::vector<uint16>&  hit_table,
	  const std::vector<uint16>&  miss_table,
	  const bool insert_free_space, ProbabilityGrid* probability_grid)

分成三部分来分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 不必关注细节，实现当前grid map边界的扩展，让它能够覆盖雷达的所有扫描数据
// 根据return, misses调整，因为新的scan加入，可能会导致地图变大
GrowAsNeeded(range_data, probability_grid);

// 这部分和 ActiveSubmaps2D::CreateGrid 对比阅读
const MapLimits& limits = probability_grid->limits();
// 构建一个分辨率更好的 Maplimits，分辨率除以1000，提高RayCasting的精度
const double superscaled_resolution = limits.resolution() / kSubpixelScale;
const MapLimits superscaled_limits(
    // 地图的x和y方向上的最大值max和原来的一样
    superscaled_resolution, limits.max(),
    // 地图格数扩展为原来的1000倍
    CellLimits(limits.cell_limits().num_x_cells * kSubpixelScale,
               limits.cell_limits().num_y_cells * kSubpixelScale)  );

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 获取激光射线的起点在精细栅格中的索引，记录在begin对象
const Eigen::Array2i begin =
    superscaled_limits.GetCellIndex(range_data.origin.head<2>());
// Compute and add the end points
std::vector<Eigen::Array2i> ends;
ends.reserve(range_data.returns.size());
// 遍历所有hit点，用容器ends记录下 所有hit点在精细栅格中的索引
for (const sensor::RangefinderPoint& hit : range_data.returns)
{
  ends.push_back(superscaled_limits.GetCellIndex(hit.position.head<2>()));
  // 查hit_table表，更新hit点 栅格概率
  // 第一个参数将精细栅格下hit点索引,重新转换成原始栅格分辨率下的索引
  // 第二个参数是待查的hit表
  // 如当前为p 则新的 p = hit_table[p]
  probability_grid->ApplyLookupTable(ends.back() / kSubpixelScale, hit_table);
}
// 如果参数 insert_free_space 为false(默认是true)，则不需要处理miss事件
if (!insert_free_space)   return;

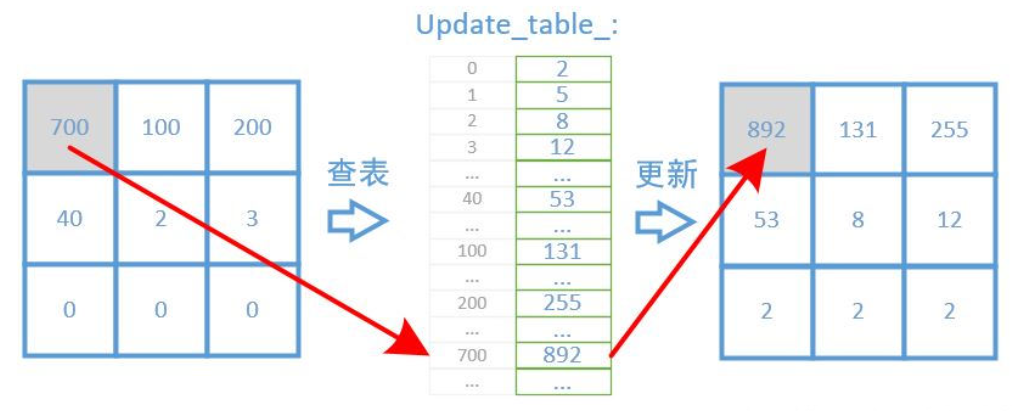
更新时，仅需查表可获得更新后的结果，而无需临时进行乘法运算

处理misses，它有两部分: origin和hit之间的栅格；激光超出max_range的栅格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 处理射线起点到hit点之间的栅格，来源还是上面的 range_data.returns
// 查找miss_table更新占用概率。这里的begin和end都是精细栅格下的索引
for (const Eigen::Array2i& end : ends)
{
  std::vector<Eigen::Array2i> ray =
      RayToPixelMask(begin, end, kSubpixelScale);
  for (const Eigen::Array2i& cell_index : ray) 
    probability_grid->ApplyLookupTable(cell_index, miss_table);
}
// 处理超出max_range的miss点，来源是 range_data.misses
// 同样认为射线起点到miss点之间的栅格发生的都是miss事件
for (const sensor::RangefinderPoint& missing_echo : range_data.misses)
{
  std::vector<Eigen::Array2i> ray = RayToPixelMask(
      begin, superscaled_limits.GetCellIndex(missing_echo.position.head<2>()),
      kSubpixelScale);
  for (const Eigen::Array2i& cell_index : ray)
      probability_grid->ApplyLookupTable(cell_index, miss_table);
}

RayToPixelMask函数实在太复杂了，知道原理即可: 使用 Bresenham 画线的方法，获取激光原点到点云之间直线的所有点坐标，前面的精细化分辨率是为了这里的画线更精确

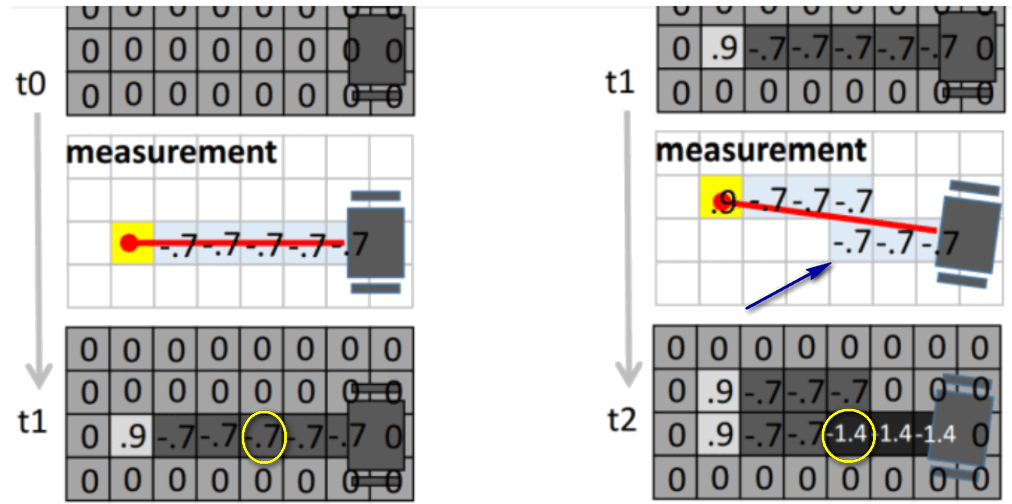
一条射线穿过很多cell，有的cell从对角穿过，有的只穿过一个小角落，虽然它们都是穿过，但是穿过的观测量不同，从对角穿过对这个cell的空闲概率的提升显然作用更大，而只穿过一个小角落显然贡献很小。

对于从对角穿过的cell，就有很多小的sub-cell落在原来的cell中，sub-cell数（记为n）越多，贡献就越大（其实就是对cell这个栅格的概率重复算了n次），而对于从小角落穿过的cell，sub-cell数就很少了.

ApplyLookupTable

查表来更新栅格单元的占用概率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// Multiple updates of the same cell will be ignored until
// FinishUpdate() is called. Returns true if the cell was updated.

// cell_index是将要更新的栅格单元索引，table是更新过程中将要查的表。
bool ProbabilityGrid::ApplyLookupTable(const Eigen::Array2i& cell_index,
                                       const std::vector<uint16>& table)
{
  DCHECK_EQ(table.size(), kUpdateMarker);
  // 然后通过 cell_index 计算栅格单元的存储索引，获取对应的空闲概率存储值
  // 并确保该值不会超出查找表的数组边界。
  const int flat_index = ToFlatIndex(cell_index);
  // 其实是 Grid2D类的成员: vector<uint16> correspondence_cost_cells_;
  uint16* cell = &(*mutable_correspondence_cost_cells())[flat_index];
  if (*cell >= kUpdateMarker)
      return false;
  // 通过父类的接口记录下当前更新的栅格单元的存储索引flat_index
  mutable_update_indices()->push_back(flat_index);
  // 通过查表更新栅格单元
  *cell = table[*cell];
  DCHECK_GE(*cell, kUpdateMarker);
  // 通过父类标记cell_index所对应的栅格的占用概率已知
  mutable_known_cells_box()->extend(cell_index.matrix());
  return true;
}


CastRays结束，最后的是FinishUpdate()

1
2
3
4
5
6
7
8
9
10
11
// 主要就是减去 kUpdateMarker
void Grid2D::FinishUpdate() {
  while (!update_indices_.empty())
  {
    DCHECK_GE(correspondence_cost_cells_[update_indices_.back()],
              kUpdateMarker);
    // ComputeLookupTableToApplyCorrespondenceCostOdds 加上了kUpdateMarker做更新标志，这里再减去
    correspondence_cost_cells_[update_indices_.back()] -= kUpdateMarker;
    update_indices_.pop_back();
  }
}

双线性插值 双三次插值|数学基础

插值指在离散数据的基础上补插连续函数，使得连续曲线 通过全部给定的离散数据点。 插值的本质 —— 利用已知数据估计未知位置数值。插值和拟合的不同之处在于：对于给定的函数，插值 要求离散点“坐落在”函数曲线上从而满足约束；而 拟合 则希望离散点尽可能地 “逼近” 函数曲线。

双线性插值 Bilinear Interpolation

一次线性插值.png
普通的线性插值我们都很熟悉。 双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
示意图.png
二次线性插值的公式.png
看这个推导

双线性插值在三维空间的延伸是三线性插值。

双三次插值 Bicubic interpolation

二维空间中最常用的插值方法。在这种方法中，函数f在点(x , y)的值可以通过矩形网格中最近的十六个采样点的加权平均得到，在这里需要使用两个多项式插值三次函数，每个方向使用一个。

双三次插值通过下式进行计算

计算系数的过程依赖于插值数据的特性。如果已知插值函数的导数，常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数与表示x与y方向的表面斜率，二阶相互导数表示同时在x与y方向的斜率。这些值可以通过分别连续对x与y向量取微分得到。对于网格单元的每个顶点，将局部坐标(0,0), (1,0), (0,1)和(1,1)带入这些方程，再解这16个方程