向量
标准化后的向量点乘得到的值为夹角的余弦。如果得到 -1, 0, -1,便可知道两个向量方向的关系是相反, 垂直, 相同
向量叉乘后得到的向量和原先两个向量垂直,也就是法向量
向量叉乘后得到的向量的模,其值为两个向量构成的三角形的面积的二倍。
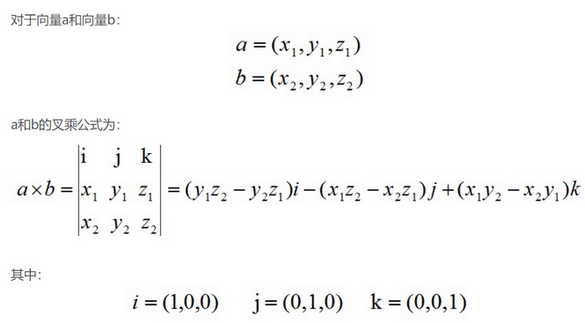
- 叉乘的一些性质

用行列式的表示方法观察,不用计算就能看出前三条。
平面的一般式
高中学过的表示方法为 ,法向量为 。这里涉及到了归一化问题,两边可以乘以系数,还是同一个平面,也可以说法向量是不唯一的。但如果给出了一般式 ,就说法向量为
空间内一点 到平面的距离是 ,如果已经归一化,那么分母就是 1
法向量可以看做平面上两个向量的叉乘。
法向量 * 距离形式
N为法向量(1x3的向量),那么[N, d]或者(N | d)为 1x4 的向量,其中d为平面到原点的距离。
旋转问题
现在平面的表示形式(无论哪种)都是基于坐标系A,另有一个坐标系B,从B到A的变换矩阵是M(4x4),那么平面在坐标系B下的表示形式是什么?
向量 ,注意不是法向量,平面上一点为 ,那么 ,经过变换后,点v变成了 ,那么有 ,也就有,因此可得 ,M矩阵的逆根据《SLAM十四讲》的公式3.13可以直接写出,最后根据 写成一般式
感觉这样推导并不严谨,但可以这样理解。
