图优化SLAM通过减去原始传感器的测量，构建了简化的估计问题。这些原始的测量由图中的边取代，边可以看做“虚拟测量”(virtual measurements)。图中的两个节点之间的边是用两个位姿之间的相对位置的概率分布表示的，这一概率分布的条件是它们的相互测量。观测模型 $p(z_t | \ x_t, m_t)$ 是多模态的，因此高斯分布的假设不成立。这意味着一次观测 $z_t$ 可能影响图中连接不同位姿的多条边。 graph connectivity 应当用概率分布来描述。如果直接处理这个多模态问题，将出现极大的复杂度。我们需要将地图变成node和edge的拓扑结构。因此，需要确定不同node之间的edge约束。

我们应当判断一次观测导致的最可能约束，这取决于机器人位姿的概率分布。这一问题称作data association，常由SLAM后端解决。前端需要对机器人轨迹 $p(X_{1:T} \ | \ Z_{1:T}, \ u_{1:T})$ 上的条件先验进行一致估计，这就要求机器人运动过程中对前端和后端穿插地执行。因此后端的准确性和效率对SLAM系统非常重要。

如果观测值受局部高斯噪声影响，而且data association已知，基于图的建图算法的目标就是机器人轨迹的高斯估计后验。包括计算这个高斯分布的均值，然后以均值作为节点的configuration，这样最大化了观测的似然。

• 图优化中，顶点是优化项，而边是约束项。优化过程就是通过全局调整优化项，使约束项的和最小。
• Pose(x)与Landmark(m)构成了图的顶点集
• 边(Edge)存在两种。第一种是Pose到Pose，另一种是Pose到 Landmark

• 图优化中边表示约束，Pose到Pose的边与机器人的运动模型相关，机器人从$x_0$运动到$x_1$，形成了这条边。同时在运动模型的作用下，可以获得机器人在$x_0$，控制量为$u_1$时的状态 g。该值与“真实”的Pose 的差，构成了这条边的约束。由于边的约束是标量，因此取这个差的平方。R表示为运动模型的协方差。公式可以写作 $(x_1 - g)^T R^{-1}(x_1 - g)$

• Pose到Landmark的边与机器人的观测模型相关，机器人从 $x_{1}$观测到 $m_{1}$，就会形成一条边。同时在观测模型 $h_{(measure, Pose)}$ 的作用下，可以获得机器人在 $x_{1}$ 时对 $m_1$ 的预测 $h_{(m_{1}, x_{1})}$。该值与此时真正观测到的值 $z_{1}$ 的差，构成了这条边的约束。同样的，取这个差的平方作为约束值。$Q$ 表示为观测模型的协方差。公式 $[z_1 - h(m_1,x_1)]^TQ^{-1}[z_1 - h(m_1,x_1)]$

• 完整的约束为两种约束的和 $J_{GraghSLAM}$

SLAM的图优化问题就是寻找合适的 Pose(x), Landmark(m)，使 $J_{GraghSLAM}$ 最小。

看到预测值和观测值的差，很容易想到Cartographer，PoseExtrapolator提供预测值，Scan Matcher提供观测值。

或者可以这样理解：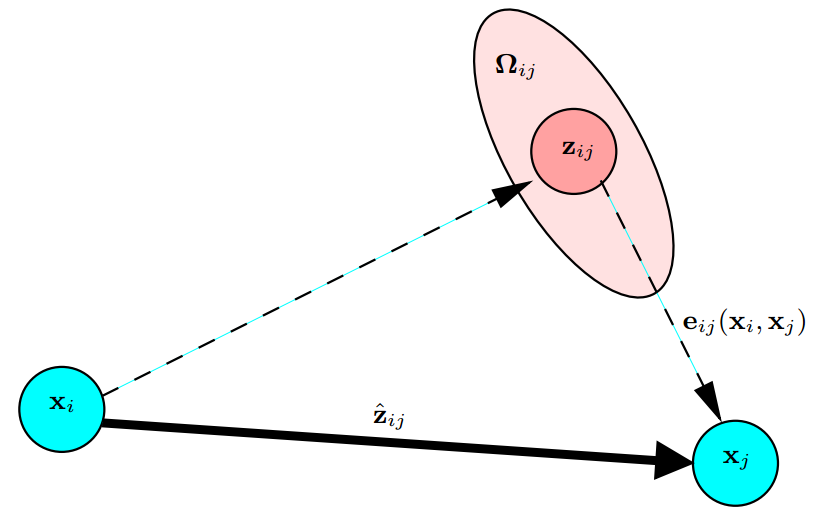


我们用$e(x_i,x_j,z_{ij})$ 表示预测值和观测值之间的差，假设其满足高斯分布 $N(0, \Sigma)$，或者说观测值的分布是以真值为中心的多元高斯分布。 我们的目标是让预测值和观测值尽可能趋近于0（均值），也就是让 $e$ 出现在概率最大的地方，这就是个最大似然的问题。 我们让概率密度函数取最大值

把图中的x换成 $e(x_i,x_j,z_{ij})$， 均值取0，得到下面的最小二乘形式

最小二乘问题的目标函数的变量维度很高，但每个误差项都是简单的，仅与少量变量有关。因此为了直观的展示变量与变量之间的关系，可以把优化问题用图的方式来展现。其中顶点表示优化变量，边表示误差项。

图优化的流程

1. 选择你想要的图里的顶点与边的类型，确定它们的参数化形式

2. 往图里加入实际的顶点和边

3. 选择初值，开始迭代

4. 每一步迭代中，计算对应于当前估计值的雅可比矩阵和海塞矩阵

5. 求解稀疏线性方程 $H_k \Delta x = -b_k$ ，得到梯度方向

6. 继续用高斯牛顿法(GN)或列文列文伯格-马夸尔特法(LM)进行迭代。如果迭代结束，返回优化值。

SLAM中的图优化

滤波类算法最大的问题，是无法处理大尺度场景的建图。由于滤波类算法是基于递归计算的，下一时刻的估计值依赖于上一时刻的估计，因而在大尺度场景下，由于系统参数和传感器观测数据的不准确性，会造成误差慢慢累积，一旦当前时刻的估计出现偏差，无法修正该误差，最终无法获得一致性的地图。

另外滤波方法对计算量和内存消耗都很大，使用图优化方法则效率较高，这种方法位姿不是实时纠正，而是将数据记录下来，最后进行计算优化。

机器人的位姿是一个顶点(vertex)，位姿之间的关系构成边(edge)，边表示两个位姿的空间约束(相对位姿和对应方差)。比如t+1时刻和t时刻之间的里程计关系构成边，或者由视觉计算出来的位姿转换矩阵也可以构成边。图构建完成后，就要调整机器人的位姿去尽量满足这些边构成的约束。图优化就是构建图并调整各顶点的位姿，使预测和观测的误差最小。每一条边的信息矩阵就是协方差矩阵的逆。协方差越小，说明这次测量越准，信息权重就越大。

前端： 从里程计和激光雷达数据中求得位姿，构建图。机器人位姿当做顶点，位姿间关系当做边，常常是传感器信息的堆积
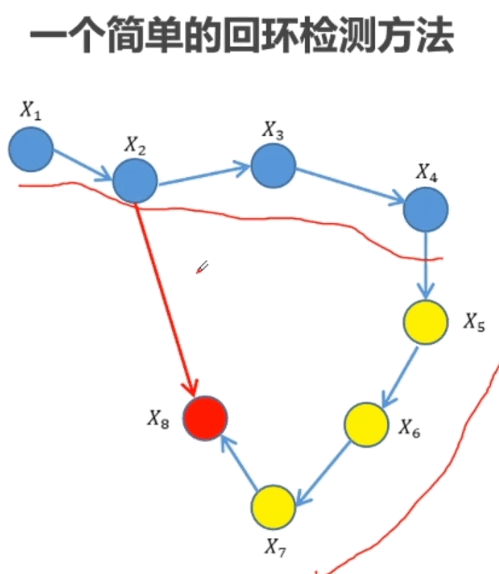
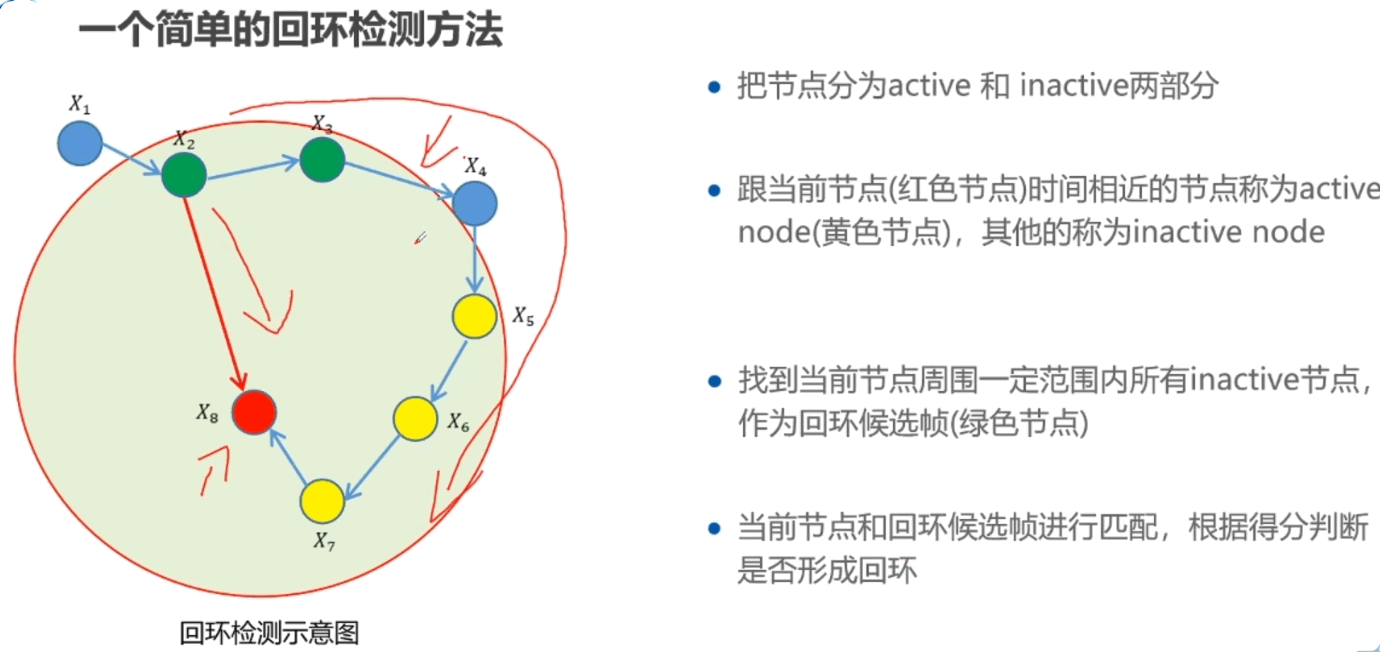
后端： 在图构建好以后，采用回环检测，出现了回环边说明有误差。构造闭环约束，调整机器人位姿，通过最小化观测和估计残差求得优化后的位姿。

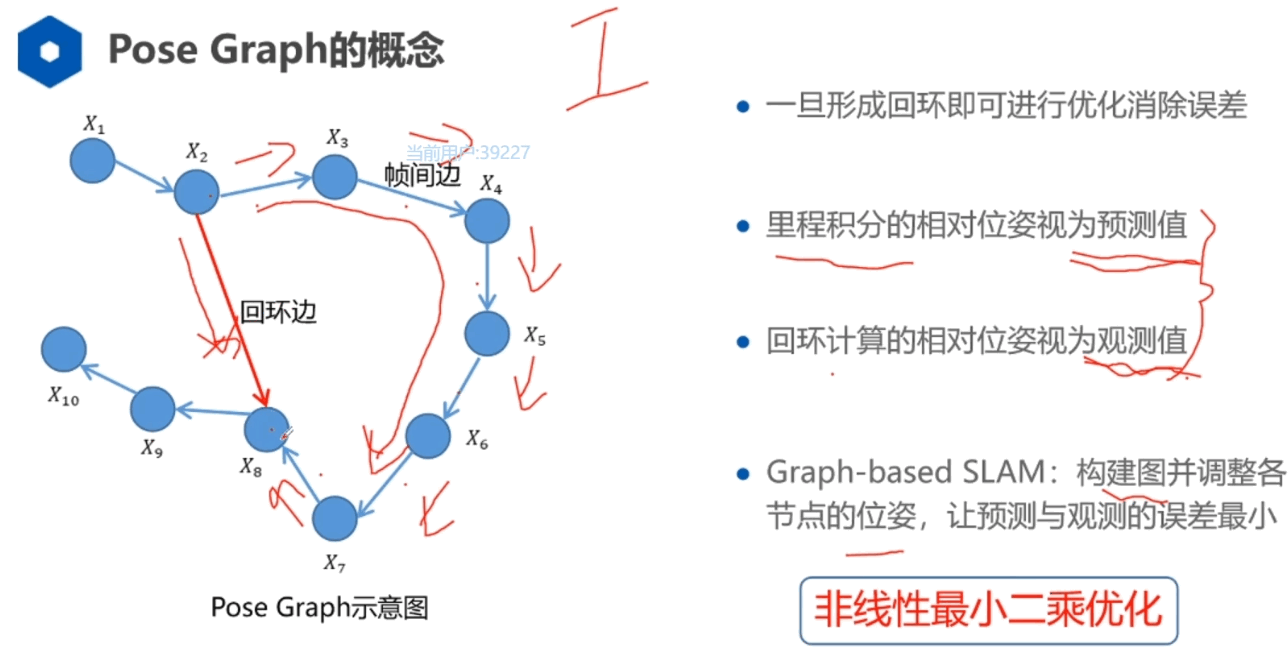
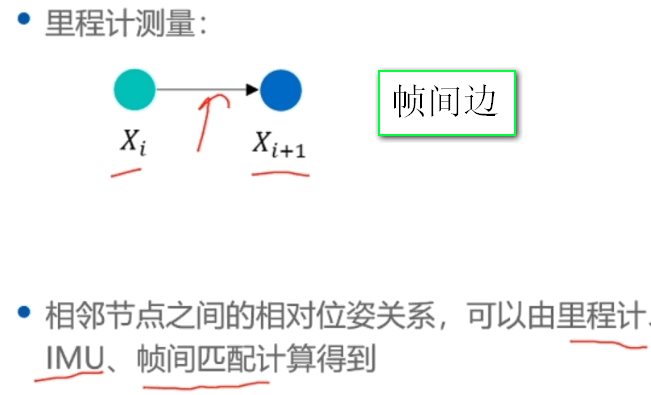
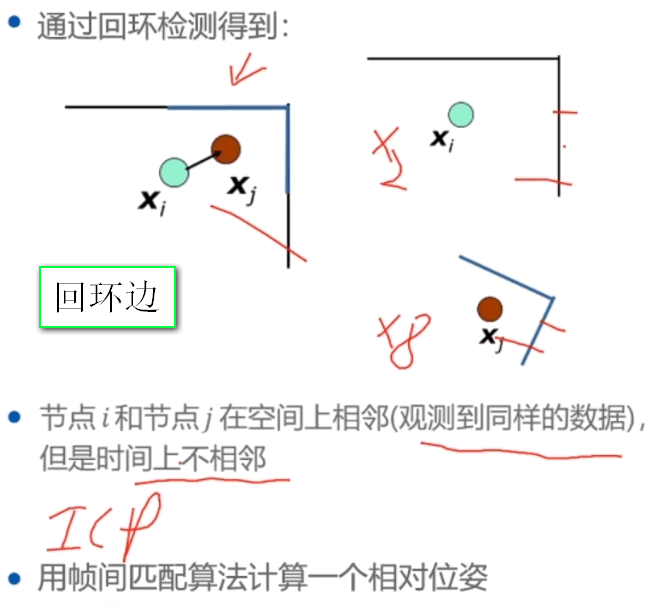
通过帧间匹配得到 $X_8$ 和 $X_2$之间的相对位姿，称为观测值

观测方程也有很多形式，如：

• 机器人两个Pose之间的变换；
• 机器人在某个Pose处用激光测量到了某个空间点，得到了它离自己的距离与角度；
• 机器人在某个Pose处用相机观测到了某个空间点，得到了它的像素坐标；

同样，它们的具体形式很多样化，这允许我们在讨论slam问题时，不局限于某种特定的传感器或姿态表达方式。

这个减法只是通用的，在SLAM里可能没有定义减法。