论文实际是关于无人机的,这里只记录有参考价值的部分。
论文提出了一种方法,即构建一个无约束的二次规划问题,对分段的多项式路径进行联合优化,这个二次规划对高次多项式和大量分段数值稳定。另一项contribution是自动选择每段的时间。使用多项式路径,不必进行大量的采样和机器人在高维状态空间的模拟。本算法不能保证渐进收敛到全局最优。
算法将搜索和优化结合起来,比纯粹基于搜索的规划算法在计算上的表现好得多。对每段时间的分配使planner能自动适应变化范围很大的size scales,只使用一个用户设置的参数
1.1 问题和方案
使用RRT*算法找到无碰撞的路径,(开始运动后可以有动态障碍)开始只考虑运动学,不考虑动力学。路径被裁剪为极少的路径点,对路径点的选取是根据line-of-sight技巧。使用分段的多项式路径插入到各路径点,生成光滑的minimum-snap路径。二次规划将路径导数(Path Derivatives)的代价函数最小化,路径的终点可以是固定值,也可以是free.(我的理解是类似三次样条曲线的自由边界) 多项式的导数连续性保证了移动的平滑性。
论文的框架:
- 先讨论无人机的模型
- 提出二次规划问题的闭式解
3. 多项式路径
要求每段的时间(vector of times)是固定的,也要预先确定。大致可以根据车的期望平均速度确定,但这样不会生成最低代价的方案。因此我们将遍历地refine时间向量。
3.5 保证轨迹是无碰撞的
如果轨迹中某一段和障碍相交了,就在这段轨迹中添加中点,将其一分为二。这个中点是无碰撞的,因为它取决于搜索算法返回的分段路径。我的理解是全局路径返回的一定是无碰撞的,在它上面取一点,肯定还是无碰撞。然后多项式路径添加中点后再次二次规划,而且这个再规划过程可能会重复,直到多项式路径无碰撞(递归取中点)。图4表示了这个过程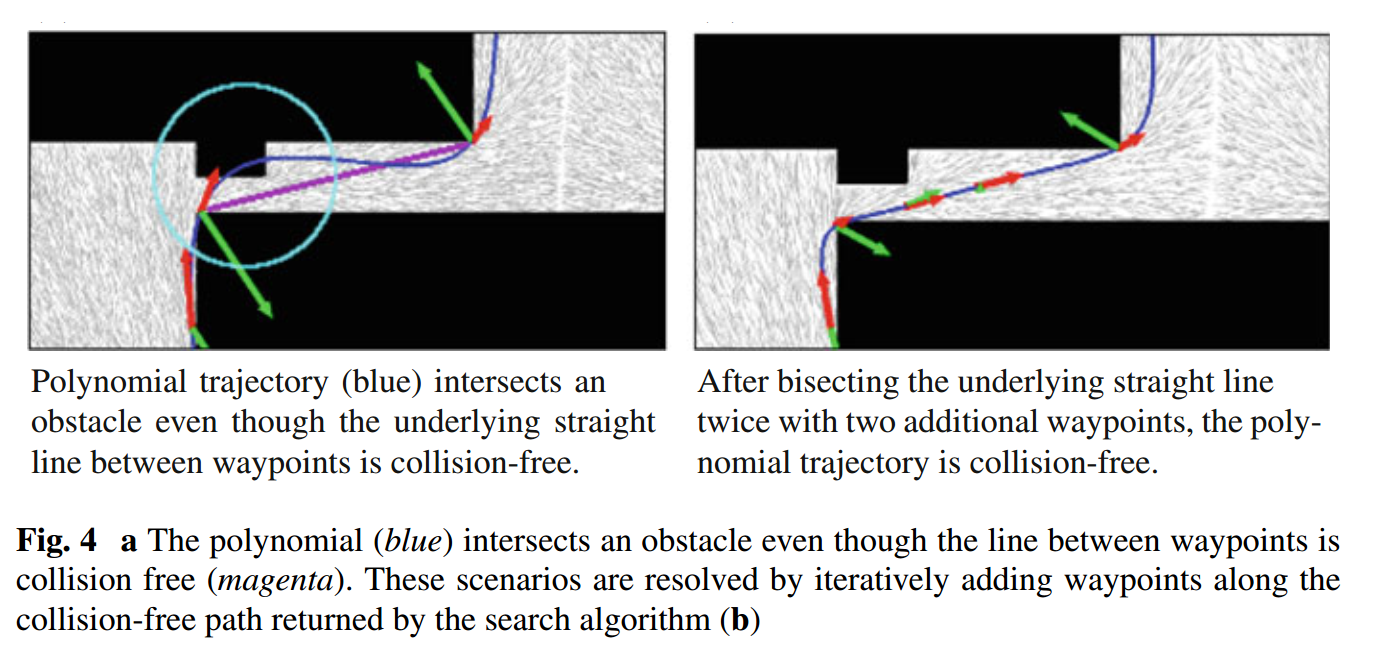
a图的直线部分本来是无碰撞的,经过优化反而碰撞了,此时就需要增加b中的两个中点
在稠密环境中,轨迹需要增加很多额外路径点以处理碰撞情况,因此二次规划会进行很多次,增加了计算量。但是根据我们在室内环境的经验,增加的路径点不会超过原有路径点的一般,所以计算量增加很少。
原理补充
设置一个目标代价函数,目的在于找到这几个变量在取一定值时使得我们设计的代价函数取得最小值。更通俗的说:就是这几个变量取一定值的时候可以使机器人能量耗费最少,或者机器人运动的转动更少等等。这种思想不仅适用于minimum snap算法。
机器人在起点和终点的速度或者加速度,我们都是可以设置的。机器人中间航迹点的位置也是需要事先给定的,但是机器人中间点的速度和加速度 Jerk等信息,我们没法去约束它,因为很难去确定机器人到达某一个点的速度或者加速度。这正是我们研究算法的目的。如果中间点的速度加速度事先设置,机器人会忽快忽慢或者速度不变,很难实现,即使能实现,也十分不美观。
因此我们认为中间点的速度、加速度等信息是一个可以自由变化的状态,那么对于这种中间状态不确定的问题,我们可以构建一个优化问题,使得中间状态取得某一个值时,我们制定的代价函数达到最小值,因此通过优化代价函数得到一个最优的轨迹。根据上面的分析,对于中间点的速度和加速度,或者更高阶的Jerk甚至Snap等,我们不对其进行微分限制,只进行连续性约束,然后让优化器给它们分配最优的状态。
minimum snap 可以理解为最小化加加加速度。
Jerk: 所受力的变化率。 (如每秒增加一牛顿)
snap: 所受力的变化率的变化。(如前一秒增加一牛顿,接下来一秒增加两N,第二秒受力与最初相比增加了三个N)
最小snap,就让jerk变化比较小。如果snap为0,就代表每秒加速度稳定增加 (受力稳定增加)。
实际工程中,对于高于加速度之后的导数,都将其设置为0,也就是最小化Snap,只需给出位置、速度、加速度的设置值,而Jerk就默认为0。
时间对于最终生成轨迹的好坏有很大影响。如果把每段时间也加入到优化的代价函数中,这样固然是好,但是势必会增加优化的时间,并且无法再闭式的求解这个问题。
梯形时间分配:先假设机器人以最大的加速度加速到最大速度,然后运行一段时间,再以最大的减速度到终点,到达是速度为0。
缺点
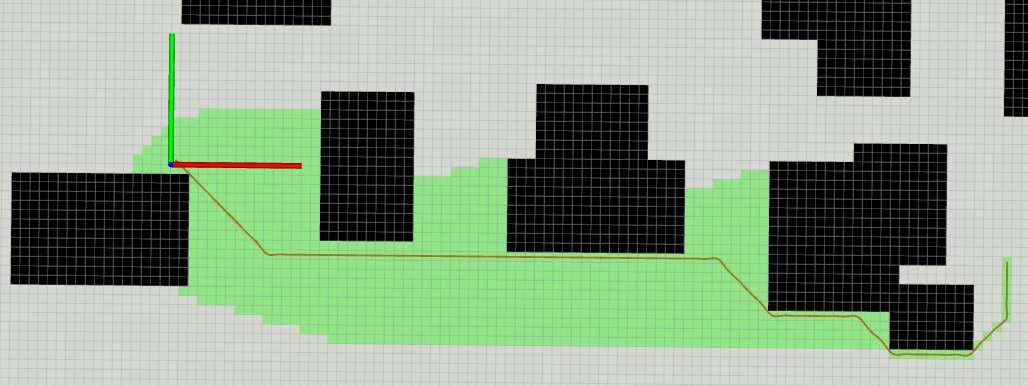
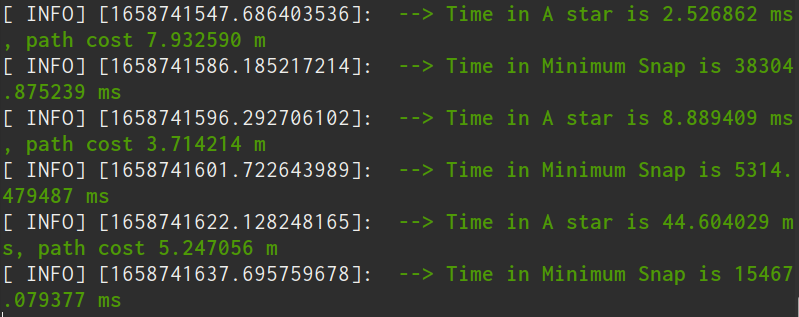
规划最小snap时,占用的CPU也比较大
矩阵求导求时,矩阵可以尝试用LLT分解等方法绕开。 最后求向量P 时的也可以尝试绕开。但是中的必须计算,这会非常耗时间。因此要看近年的论文。
