SLAM前端匹配,是构建方程的过程。后端优化是求解方程的过程。一个好的SLAM算法重点在前端。
做帧间的匹配是为了得到机器人前后的局部位姿变换关系,可以认为是一种里程计。其实标定了轮子直径跟间距我们就有了一个里程计了,但是因为轮子打滑等各种因素存在误差会比较大。再用雷达的数据做一次配准可以提高定位精度。
- ICP:迭代最近点
- PL-ICP:点到线的ICP
- IMLS-ICP:implicit moving least square,隐式移动最小二乘
- Generalized ICP (GICP),综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略,精度、鲁棒性都有所提高;
Normal Iterative Closest Point (NICP) - NICP:考虑法向量和局部曲率,更进一步利用了点云的局部结构信息,其论文中实验结果比 GICP 的性能更好。

ICP
R,t就是相邻两帧激光对应的机器人位置的欧氏变换,以此类推,根据很多帧的点云,就能求出一系列的机器人位姿变换关系。
ICP有二维和三维。
由于两个点云对应同一个实体,那么理论上配准后的距离应该为0,由于误差的存在,我们要求距离的最小值。
对于已知对应点的情况(已知R),我们可以求出闭式解,而不必用迭代方法: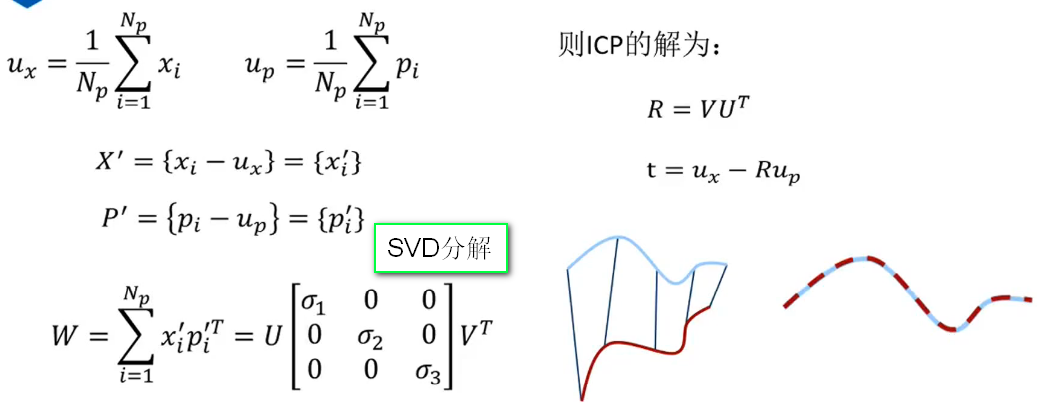
实际中不知道对应点匹配,不能直接算出R和t,要进行迭代计算:寻找对应点,根据对应点计算R,t;对点云转换再计算误差;不断迭代直至误差足够小。ICP算法里不能有nan的雷达数据
ICP方法存在以下缺点,所以不在实际SLAM中使用:
- 依赖初始值,初始值不好时,迭代次数增加;对于较大的初始误差,可能会出现错误的迭代结果
- ICP是一阶收敛,收敛速度慢。(所以会用kd-tree来加快搜索效率)例如我使用A2雷达,频率12.7Hz,两帧间隔0.079s。ICP时间在
0.01s~0.02s,而超过0.015s的有一部分,这就了两帧scan间隔的%19。甚至有些雷达,ICP计算时间大于两帧间隔,这样算出来的位置始终是延迟的. - 两帧激光点云中的点不可能表示的是空间中相同的位置,所以用点到点的距离作为误差方程势必会引入随机误差。
- 会有离群点及噪声
所以原始的ICP太粗糙,不足以应用实践。
PL-ICP
深蓝学院这一段又讲的不好,对censi论文中的PL-ICP示意图讲解不到位,对红色和蓝色的点,同心圆没有说明,而且数学公式怀疑有问题,看的云里雾里。
Point to Line-ICP修改的是误差尺度,思想和之后的ICP类似。
雷达的激光点是对实际环境中曲面的离散采样。重要的不是激光点,而是曲面。最好的误差尺度为当前激光点到实际
曲面的距离;所以关键的问题在于如何恢复曲面
PL-ICP:用分段线性的方法(折线)来对实际曲面进行近似,从而定义当前帧激光点到曲面的距离
- ICP对点对点的距离作为误差,PL-ICP为点到线的距离作为误差;PL-ICP的误差形式更符号实际情况。
- 收敛速度不同,ICP为一阶收敛,PL-ICP为二阶收敛。
- PL-ICP的求解精度高于ICP,特别是在结构化环境中,但不适合室外
- PL-ICP对初始值更敏感。不单独使用,其容易陷入局部循环。与里程计、CSM等一起使用,通常用里程计得到一个初始转换矩阵q0给到PL-ICP算法
经我测试,换成PL-ICP后,配准时间降了一个数量级,耗时比较长的是0.00274035s。但是静止时输出的帧间匹配结果的精度,没有明显提升,可能是雷达问题。
ros的csm包实现了ICP和PL-ICP算法。作者给出了一个该功能包的操作说明文件(csm_manual.pdf)。里面详细描述了各项配置参数的含义。其中sm/app文件夹中的sm0.c sm1.c sm2.c sm3.c 相当于是几个使用示例。 主要的算法实现是在csm/icp文件夹中的几个文件里。论文中的所有算法步骤完整的体现在了icp_loop.c文件中的icp_loop函数里。
