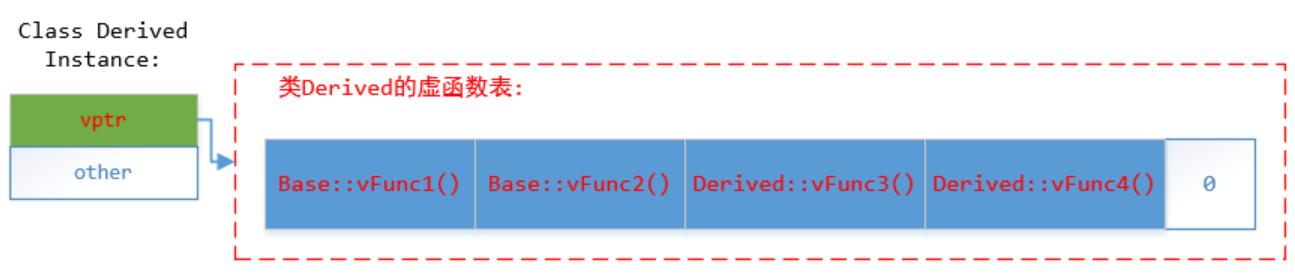
std::begin() 和 std::end() std::begin()和std::end()是STL中的函数模板,用于获取容器(数组、std::initializer_list、STL标准容器、std::string_view、std::array等)的起始和结束迭代器。它们提供了一种通用的方式来访问这些序列的边界,而不依赖于具体的容器类型。一般结合STL的算法一起使用
1 2 int a[] = { 1 , 3 , 5 , 2 , 9 , 6 , 8 };std::sort (std::begin (a), std::end (a) );
感觉和现有的begin,end迭代器有些冗余
std::find find() 函数是一个泛型算法,可以用于操作所有STL容器。它用于在数组或标准库容器(如vector, map)中查找指定元素,查找成功则返回一个指向指定元素的迭代器,查找失败则返回end迭代器。注意: 不是返回 true or false
时间复杂度是O(n) 1 2 3 4 5 6 7 8 9 10 vector<int > num_list = { 2 ,4 ,6 ,8 ,10 ,12 }; int find_num = 8 ; std::vector<int >::iterator num = std::find (num_list.begin (), num_list.end (), find_num); if (num != num_list.end ()) { cout << "其索引为 " << distance (num_list.begin (), num) << endl; } else cout<< "元素 " << find_num << " 不在num_list中" << endl;
map::find 和 set::find,由于map和set内部是红黑树实现的。因此map和set内部的find函数查找时间复杂度是 O(logn)
copy std::copy(start, end, container.begin());
copy只负责复制,不负责申请空间,所以复制前必须有足够的空间。如果container的大小小于输入序列的长度N的话,这段代码会导致崩溃(crash)。所以此时引入了back_inserter1 std::copy (src.begin (), src.end (), std::back_inserter (dest));
back_insert_iterator迭代器,这样,复制的元素都被追加到container的末尾了。(就算container为空也没事)。
1 2 3 4 5 6 7 8 9 10 11 vector<int > vec; vec.push_back (1 ); vec.push_back (2 ); vec.push_back (3 ); vec.push_back (4 ); vec.push_back (5 ); vector<int > vv; std::copy (vec.begin (), vec.end (), std::back_inserter (vv) ); for (const auto &it: vv) cout << it << " " ;
fill std::fill 是C++标准库中的一个函数,和copy相对。定义在 头文件中。它将指定的值赋给一个给定范围内的所有元素,常用于数据结构初始化,可以用于vector, list和数组。
1 2 std::vector<int > vec = {1 , 2 , 3 , 4 , 5 }; std::fill (vec.begin (), vec.end (), 0 );
使用之前,必须对vector分配内存,比如调用resize函数。
std::fill有很多重载形式,但最常用的是根据容器迭代器赋值的形式。
std::distance 用于计算两个迭代器之间的距离。它提供了一种方便的方法处理迭代器范围时进行遍历和计算。它在头文件<iterator>中定义,函数原型如下:1 2 3 template < class InputIt >typename std::iterator_traits<InputIt>::difference_type distance ( InputIt first, InputIt last ) ;
1 2 std::vector<int > v{3 , 1 , 4 , 1 , 5 , 9 }; std::cout << "distance: " << std::distance (v.begin (), v.end ()) << std::endl;
std::distance()函数计算的是迭代器之间的距离,而不是元素的个数。因此,在使用时需要确保迭代器范围有效,否则可能导致未定义行为。std::distance的时间复杂度为O(N),其中N是迭代器范围内的元素数量。对于随机访问迭代器(如指针、数组等),时间复杂度为O(1)
reverse 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <vector> #include <iostream> #include <iterator> #include <algorithm> int main () std::vector<int > v ({1 ,2 ,3 }) ; std::reverse (std::begin (v), std::end (v)); std::cout << v[0 ] << v[1 ] << v[2 ] << '\n' ; int a[] = {4 , 5 , 6 , 7 }; std::reverse (std::begin (a), std::end (a)); std::cout << a[0 ] << a[1 ] << a[2 ] << a[3 ] << '\n' ; }
cmp函数 cmp 函数的特点:
返回值为 bool 类型,用来表示当前的排序是否正确
参数为两个相同类型的变量,且类型与要排序的容器模板类型相同1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 bool cmp ( const Data& d1, const Data& d2) return (d1 <= d2); } vector<Data> vec; Data temp; for ( int i = 0 ; i < 8 ; ++i ){ temp.dist = rand () %50 ; temp.confidence = 100 ; vec.push_back ( temp ); } for (int i=0 ; i<8 ; i++){ cout << vec.at (i).dist << " " ; } cout << endl; stable_sort ( vec.begin (), vec.end (), cmp );for (int i=0 ; i<8 ; i++){ cout << vec.at (i).dist << " " ; }
std::accumulate 函数 用来计算特定范围内(包括连续的部分和初始值)所有元素的和,除此之外,还可以用指定的二进制操作来计算特定范围内的元素结果,需要 #include <numeric>。 三个形参:头两个形参指定要累加的元素范围,第三个形参则是累加的初值。
1 2 3 4 5 6 7 8 9 10 11 12 13 vector<int > vec; vec.push_back (1 ); vec.push_back (2 ); vec.push_back (3 ); vec.push_back (4 ); vec.push_back (5 ); for (const auto &it: vec){ cout << it << " " ; } cout << endl; int num = std::accumulate (vec.begin (), vec.end (), 0 , [](int input){return 2 *input; } );
我们期待的结果是num为30,但是这样会报错 candidate: main()::<lambda(int)> int num = std::accumulate(vec.begin(), vec.end(), 0, [](int input){return 2*input; } );
^ candidate expects 1 argument, 2 provided
最后一句应该改为 int num = std::accumulate(vec.begin(), vec.end(), 0, [](int n, int input){return n + 2*input; } );,得到num为30
sort sort使用快速排序的递归形式,时间复杂度是O(nlog(n) )
Sort函数有三个参数:(第三个参数可不写)
第一个是要排序的数组的起始地址。
第二个是结束的地址(最后一位要排序的地址)
第三个参数是排序的方法,可以是从大到小也可是从小到大,还可以不写第三个参数,此时默认的排序方法是从小到大排序。
1 2 3 int b = 3 , c = 12 ;qDebug () << std::greater<int >()(b, c);qDebug () << std::less<int >()(b, c);
1 2 3 4 5 6 7 8 int a[]={3 ,4 ,1 ,12 ,0 ,8 ,4 };std::sort (a, a+7 ); std::sort (a, a+7 , std::greater<int >()); for (int i=0 ; i < 7 ; i++) cout << a[i] <<" " ;
使用Lambda表达式作为排序标准1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 vector<int > vec; vec.push_back (1 ); vec.push_back (2 ); vec.push_back (3 ); vec.push_back (4 ); vec.push_back (5 ); for (const auto &it: vec){ cout << it << " " ; } cout << endl; std::sort (vec.begin (), vec.end (), [](int a, int b){ return 2 ) < (b%2 ); } ); for (auto it : vec){ cout << it << " " ; }
针对自定义的数据类型,需要自定义排序的方式1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 struct Frontier { Frontier (double c): cost (c){} double cost; }; bool compareFrontier (Frontier f1, Frontier f2) return (f1.cost < f2.cost); } void showFrontiers (const vector<Frontier>& v) for (auto f: v) cout << f.cost << " " ; cout << endl; } vector<Frontier> frontiers; frontiers.push_back (Frontier (1.2 ) ); frontiers.push_back (Frontier (4.9 ) ); frontiers.push_back (Frontier (12.7 ) ); frontiers.push_back (Frontier (0.3 ) ); frontiers.push_back (Frontier (3.6 ) ); showFrontiers (frontiers);std::sort (frontiers.begin (), frontiers.end (), [](const Frontier& f1, const Frontier& f2) { return f1.cost < f2.cost; }); showFrontiers (frontiers);
frontiers一般用vector或数组,不能是list, dequeue, queue
运行结果:1 2 1.2 4.9 12.7 0.3 3.6 0.3 1.2 3.6 4.9 12.7