添加编译参数，例如：

• add_definitions(-DDEBUG)将在gcc命令行添加 DEBUG 宏定义；
• add_definitions(“-Wall -ansi –pedantic –g”)

编译时有时出现报警warning: extra ‘;’ [-Wpedantic]，很影响看编译信息，可使用下面方法禁止pedantic

1
2
3
4
5
6
7
8
9
10

//save compiler switches
#pragma GCC diagnostic push
#pragma GCC diagnostic ignored "-Wpedantic"

//Bad headers with problem goes here
#include <ros/ros.h>
#include <sensor_msgs/LaserScan.h>

//restore compiler switches
#pragma GCC diagnostic pop

保存文件

Node::SerializeState —— MapBuilder::SerializeState —— MapBuilder::SerializeState —— cartographer\io\internal\mapping_state_serialization.cc文件中的WritePbStream函数

实际是MapBuilderBridge::SerializeState，Node::HandleWriteState调用的也是这个函数。在最新版本里是bool MapBuilderBridge::SerializeState(const std::string& filename, const bool include_unfinished_submaps);

1
2
3

cartographer::io::ProtoStreamWriter writer(filename);
map_builder_->SerializeState(&writer);
return writer.Close();

1
2
3
4
5
6

void MapBuilder::SerializeState(bool include_unfinished_submaps,
                                io::ProtoStreamWriterInterface* const writer)
{
  io::WritePbStream(*pose_graph_, all_trajectory_builder_options_, writer,
                    include_unfinished_submaps);
}

WritePbStream如下，这里的writer就是类ProtoStreamWriter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

void WritePbStream(
    const mapping::PoseGraph& pose_graph,
    const std::vector<mapping::proto::TrajectoryBuilderOptionsWithSensorIds>&
        trajectory_builder_options,
    ProtoStreamWriterInterface* const writer, bool include_unfinished_submaps)
{
  writer->WriteProto(CreateHeader());
  writer->WriteProto(
      SerializePoseGraph(pose_graph, include_unfinished_submaps));
  writer->WriteProto(SerializeTrajectoryBuilderOptions(
      trajectory_builder_options,
      GetValidTrajectoryIds(pose_graph.GetTrajectoryStates())));

  SerializeSubmaps(pose_graph.GetAllSubmapData(), include_unfinished_submaps,
                   writer);
  SerializeTrajectoryNodes(pose_graph.GetTrajectoryNodes(), writer);
  SerializeTrajectoryData(pose_graph.GetTrajectoryData(), writer);
  SerializeImuData(pose_graph.GetImuData(), writer);
  SerializeOdometryData(pose_graph.GetOdometryData(), writer);
  SerializeFixedFramePoseData(pose_graph.GetFixedFramePoseData(), writer);
  SerializeLandmarkNodes(pose_graph.GetLandmarkNodes(), writer);
}

ProtoStreamWriter保存数据时用到了common::FastGzipString函数，实质是boost::iostreams::gzip_compressor

读pbstream文件

这个就参考纯定位流程，Node::LoadState —— MapBuilderBridge::LoadState —— MapBuilder::LoadState

MapBuilderBridge::LoadState(const std::string& state_filename, bool load_frozen_state)使用ProtoStreamReader

1
2

cartographer::io::ProtoStreamReader stream(state_filename);
map_builder_->LoadState(&stream, load_frozen_state);

另外可以参考pbstream_main.cc

安装

1
2
3
4
5
6
7
8

# 添加docker的GPG公匙
curl -fsSL https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu/gpg | sudo apt-key add -    
# 添加中科大源
sudo add-apt-repository "deb [arch=amd64] https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu $(lsb_release -cs) stable"
sudo apt-get update 
apt-cache policy docker-ce
sudo apt-get install -y docker-ce
docker version   #查看版本

镜像

• docker load -i 本地文件名    把本地文件做成image

• 执行docker images，出现下面结果

1
2
3
4

REPOSITORY   TAG          IMAGE ID       CREATED        SIZE
ros2         jazzy-full   15b1a367ae86   3 weeks ago    4.45GB
hello        gazebo       7ca40590c2f8   7 months ago   5.12GB
<none>       <none>       a4c6cd090ec3   2 years ago    4.34GB

对第一个镜像设置tag: docker tag 15b1a367ae86 ros2:jazzy-full

• docker rmi IMAGE_ID      删除镜像

容器

• docker ps -a     查看所有容器，包括已经退出的，对不需要的可以删除

• 删除容器: docker rm CONTAINER_ID

• docker start ed86d97c09bd     启动已经停止的容器

• docker stop ed86d97c09bd     停止容器

• docker run --name ubuntu -p 3306:3306 -p 22000:22 -it django_lesson:1.0     -it 表示以交互模式运行容器，通常用于进入容器内部进行操作

• 进入容器: docker run -it a4c6cd090ec3 bash，但是如果在另一个终端再次运行这个命令，进入的不是同一个容器

• 如果要在另一个终端进同一个容器，使用 docker exec -it CONTAINER_ID /bin/bash

docker build

• docker build 命令从 Dockerfile 和上下文构建镜像。Dockerfile往往是镜像需要安装的一些库和依赖项

• docker build .， 指定 PATH ，因此本地目录中的所有文件都会被延迟并发送到 Docker 守护程序

• docker build -f /path/to/a/Dockerfile . 指定dockerfile，不指定的话，默认会读取上下文路径下的 dockerfile

问题

解决Docker运行命令时提示 Got permission denied while trying to connect to the Docker daemon socket

1
2
3
4

sudo groupadd docker     #添加docker用户组
sudo gpasswd -a $USER docker     #将登陆用户加入到docker用户组中
newgrp docker     #更新用户组
docker ps    #测试docker命令是否可以使用sudo正常使用

从Docker镜像中导出文件

1. 从运行的容器中复制

先把镜像跑起来，然后从运行起来的容器中复制文件出来，复制命令如下：

1
2

# 从容器复制文件或目录到宿主机器
docker cp 6619ff360cce:/opt/h2-data/pkslow ./

1. 解压镜像tar文件

首先，第一种方法并不是万能的，因为有些镜像过于简单，少了许多基础命令，以至于无法复制文件，也无法进入shell环境。其次，要运行起来再操作，也有点占用资源，比较麻烦。

以ghcr.io/kedacore/keda:2.2.0为例演示如下从该镜像中提取文件：

（1）将镜像保存为tar文件

1

docker save -o keda.tar ghcr.io/kedacore/keda:2.2.0

（2）解压tar文件

1
2
3
4
5
6
7
8
9
10
11
12
13

tar xvf keda.tar

x 42b88f0429143256463a478dda36b5e6d63f6dc43e033c3415414149c8c3257b.json
x 82a2e23fb9f1f5ac86b6c60196bff58e163601e5f37f1bc2bb1bd1781e8f6906/
x 82a2e23fb9f1f5ac86b6c60196bff58e163601e5f37f1bc2bb1bd1781e8f6906/VERSION
x 82a2e23fb9f1f5ac86b6c60196bff58e163601e5f37f1bc2bb1bd1781e8f6906/json
x 82a2e23fb9f1f5ac86b6c60196bff58e163601e5f37f1bc2bb1bd1781e8f6906/layer.tar
x ec12616cdd736751f41ba8d32cb9e9553ec33fc9d0bd1df92d4d8995b3dbc8ea/
x ec12616cdd736751f41ba8d32cb9e9553ec33fc9d0bd1df92d4d8995b3dbc8ea/VERSION
x ec12616cdd736751f41ba8d32cb9e9553ec33fc9d0bd1df92d4d8995b3dbc8ea/json
x ec12616cdd736751f41ba8d32cb9e9553ec33fc9d0bd1df92d4d8995b3dbc8ea/layer.tar
x manifest.json
x repositories

可以看到每个分层的信息，我们查看manifest.json可以看到具体哪个layer是最新的。

（3）找其中一个layer再解压

1
2

tar xvf ec12616cdd736751f41ba8d32cb9e9553ec33fc9d0bd1df92d4d8995b3dbc8ea/layer.tar
x keda

这样，我们就获取到了keda这个可执行文件。每层的打包内容不一样，需要看所需的文件在哪个Layer。

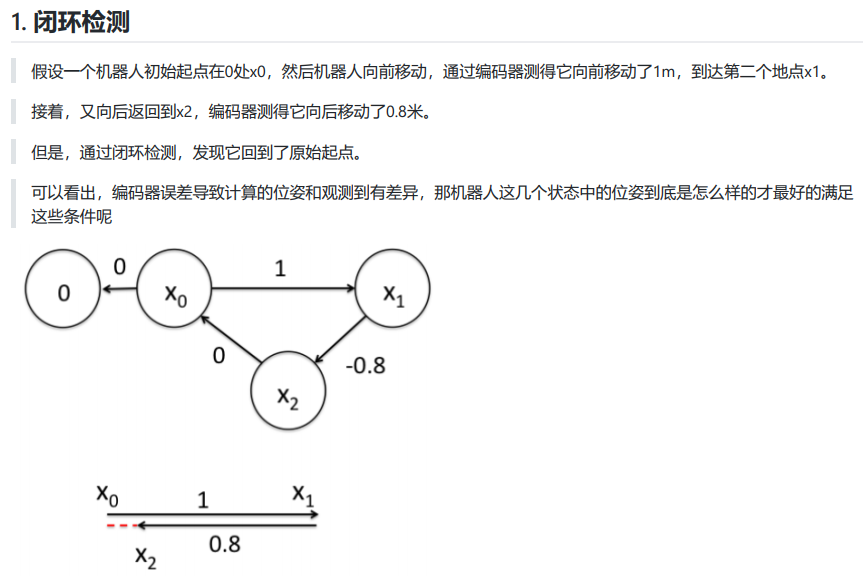
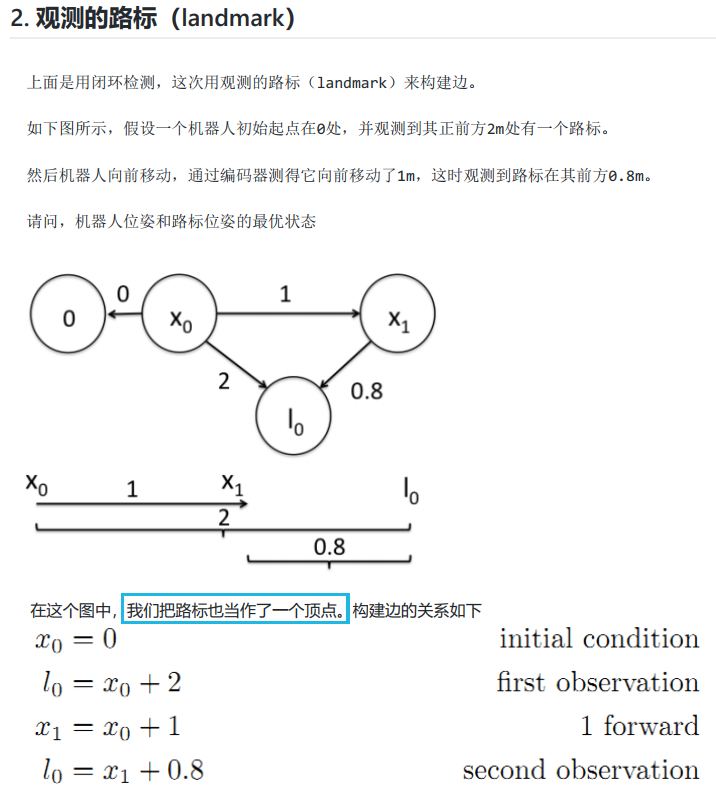
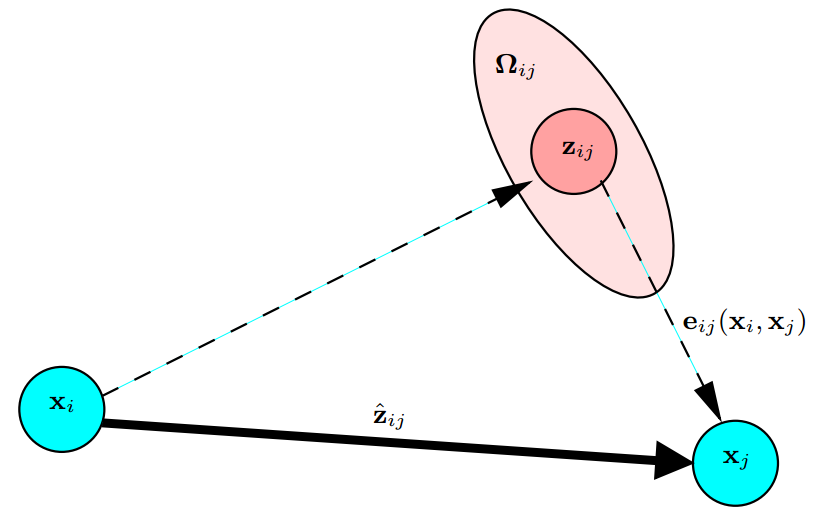
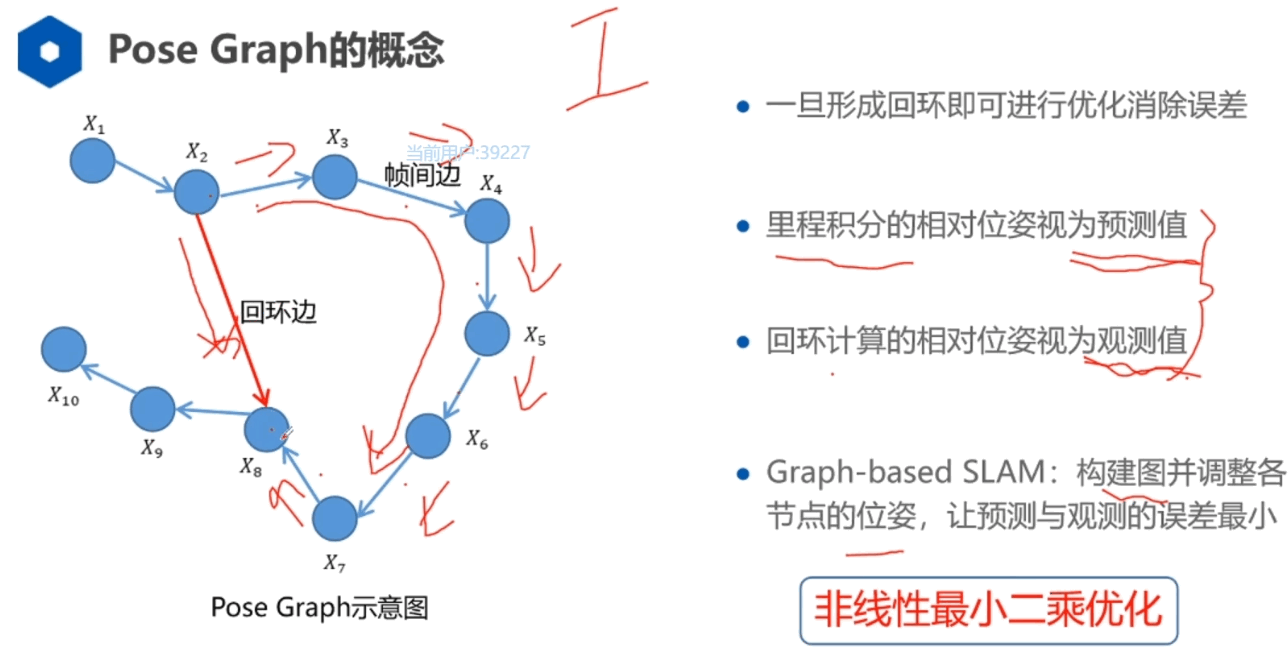
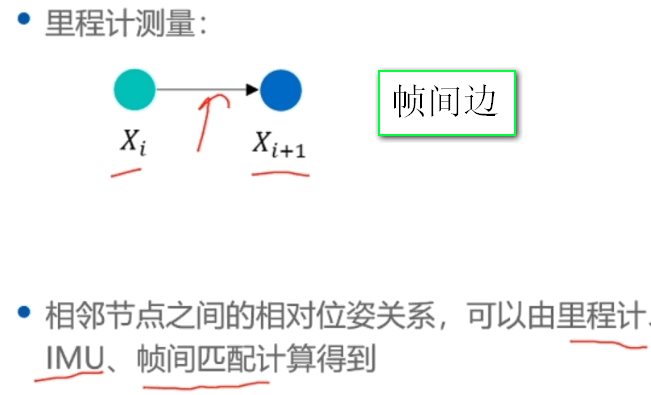
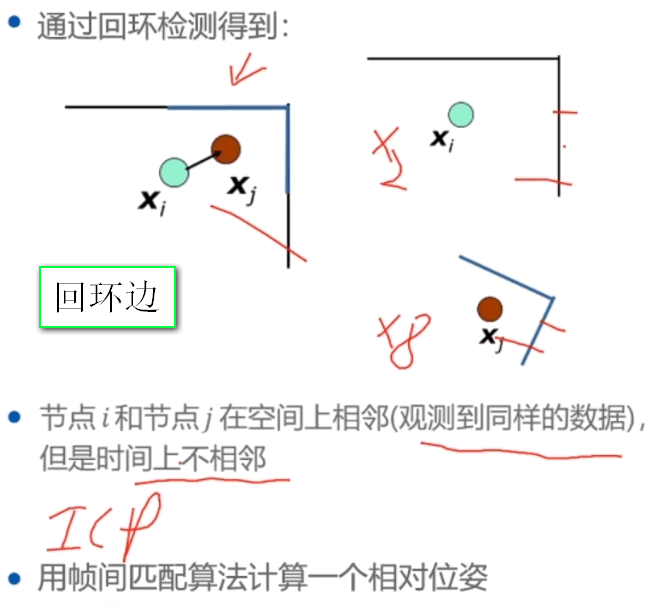
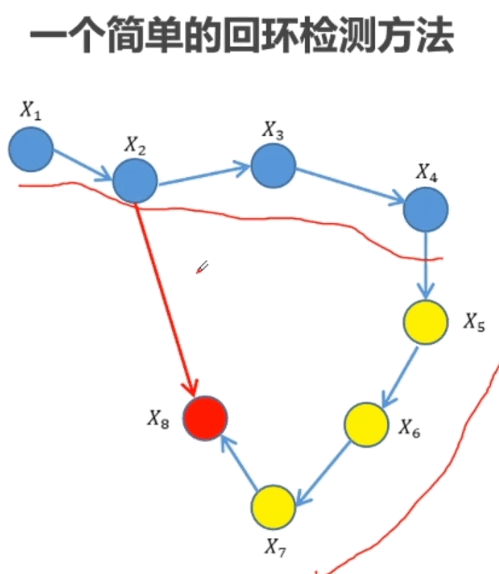
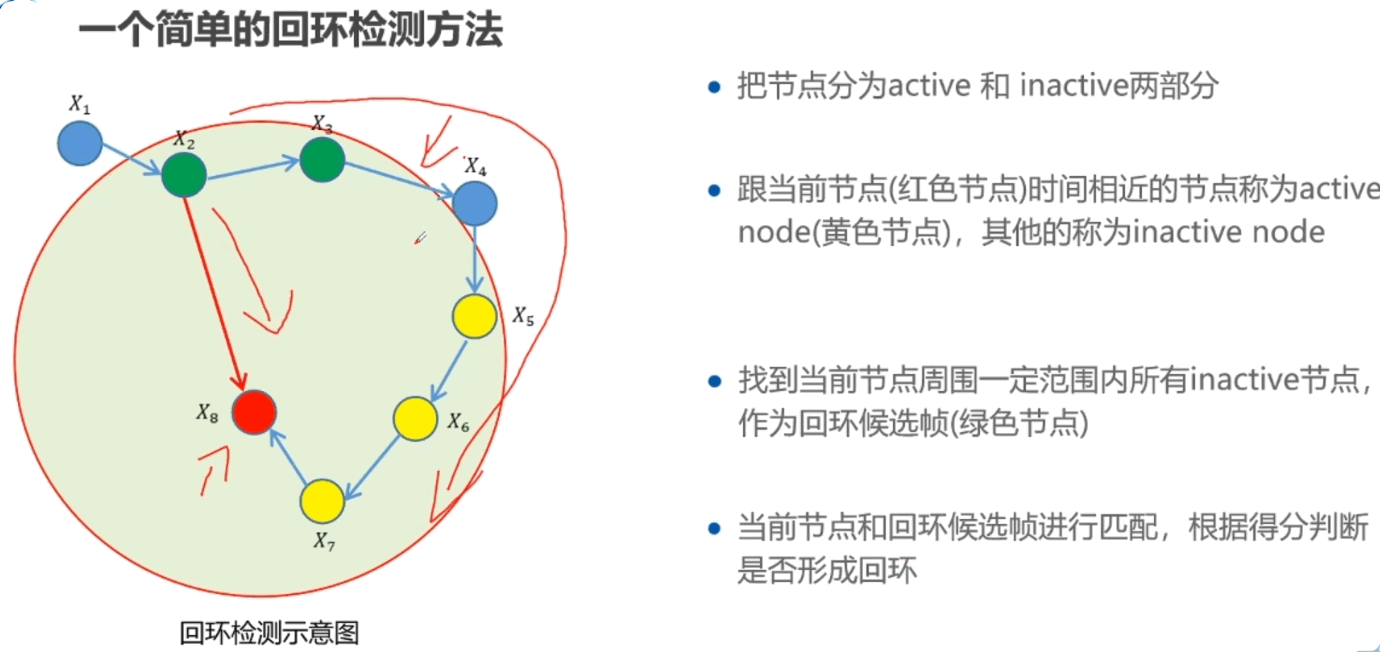
纯定位其实就是SLAM，只是不保存所有子图。因为node_main.cc里会先要运行map_builder，然后再是node.LoadState，最后StartTrajectoryWithDefaultTopics进行建图

Node::LoadState(const std::string& state_filename, const bool load_frozen_state) —— map_builder_bridge_.LoadState —— map_builder.LoadState

MapBuilder::AddTrajectoryBuilder中有一句MaybeAddPureLocalizationTrimmer(trajectory_id, trajectory_options, pose_graph_.get() );，实际就是

1
2
3
4
5
6

if (trajectory_options.has_pure_localization_trimmer()) 
{
  pose_graph->AddTrimmer(absl::make_unique<PureLocalizationTrimmer>(
      trajectory_id,
      trajectory_options.pure_localization_trimmer().max_submaps_to_keep() )  );
}

初值的处理

1
2
3
4
5
6
7
8
9

if (trajectory_options.has_initial_trajectory_pose())
{
    const auto& initial_trajectory_pose =
        trajectory_options.initial_trajectory_pose();
    pose_graph_->SetInitialTrajectoryPose(
        trajectory_id, initial_trajectory_pose.to_trajectory_id(),
        transform::ToRigid3(initial_trajectory_pose.relative_pose()),
        common::FromUniversal(initial_trajectory_pose.timestamp()) );
}

MapBuilder::LoadState

先是轨迹ID的增加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

std::map<int, int> trajectory_remapping;
for (int i = 0; i < pose_graph_proto.trajectory_size(); ++i)
{
  auto& trajectory_proto = *pose_graph_proto.mutable_trajectory(i);
  const auto& options_with_sensor_ids_proto =
      all_builder_options_proto.options_with_sensor_ids(i);
  // 新的轨迹id
  const int new_trajectory_id =
      AddTrajectoryForDeserialization(options_with_sensor_ids_proto);

  CHECK(trajectory_remapping
            .emplace(trajectory_proto.trajectory_id(), new_trajectory_id)
            .second)
      << "Duplicate trajectory ID: " << trajectory_proto.trajectory_id();
  trajectory_proto.set_trajectory_id(new_trajectory_id);

  if (load_frozen_state) {
    pose_graph_->FreezeTrajectory(new_trajectory_id);
  }
}

以添加子图为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

io::ProtoStreamDeserializer deserializer(reader);

// Create a copy of the pose_graph_proto, such that we can re-write the
// trajectory ids.
proto::PoseGraph pose_graph_proto = deserializer.pose_graph();
const auto& all_builder_options_proto =
//  子图位姿
MapById<SubmapId, transform::Rigid3d> submap_poses;
for (const proto::Trajectory& trajectory_proto :
     pose_graph_proto.trajectory())
{
  for (const proto::Trajectory::Submap& submap_proto :
       trajectory_proto.submap())
  {
    submap_poses.Insert(SubmapId{trajectory_proto.trajectory_id(),
                                 submap_proto.submap_index()},
                        transform::ToRigid3(submap_proto.pose()));
  }
}
MapById<SubmapId, mapping::proto::Submap> submap_id_to_submap;
// while 读子图数据
proto.mutable_submap()->mutable_submap_id()->set_trajectory_id(
    trajectory_remapping.at(
        proto.submap().submap_id().trajectory_id()));
submap_id_to_submap.Insert(
    SubmapId{proto.submap().submap_id().trajectory_id(),
             proto.submap().submap_id().submap_index()},
    proto.submap());
// 进入后端
for (const auto& submap_id_submap : submap_id_to_submap) {
  pose_graph_->AddSubmapFromProto(submap_poses.at(submap_id_submap.id),
                                  submap_id_submap.data);
}

后端的处理

1
2
3
4
5
6
7
8
9
10

void PoseGraph2D::AddTrimmer(std::unique_ptr<PoseGraphTrimmer> trimmer)
{
    PoseGraphTrimmer* const trimmer_ptr = trimmer.release();
    AddWorkItem([this, trimmer_ptr]() LOCKS_EXCLUDED(mutex_)
    {
      absl::MutexLock locker(&mutex_);
      trimmers_.emplace_back(trimmer_ptr);
      return WorkItem::Result::kDoNotRunOptimization;
    });
}

这里作为WorkItem加入到了队列里，到了HandleWorkQueue才处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// 纯定位时，子图的裁剪，如果没有裁剪器就不裁剪
TrimmingHandle trimming_handle(this);
for (auto& trimmer : trimmers_)
{
	// 这里实际就是 PureLocalizationTrimmer::Trim
	trimmer->Trim(&trimming_handle);
}
// 裁剪器完成状态，删除裁剪器
trimmers_.erase(
    std::remove_if(trimmers_.begin(), trimmers_.end(),
                   [](std::unique_ptr<PoseGraphTrimmer>& trimmer) {
                     return trimmer->IsFinished();
                   }),
    trimmers_.end());

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

void PureLocalizationTrimmer::Trim(Trimmable* const pose_graph)
{ 
  // trajectory 是FINISHED状态，或者没有 trajectory
  if (pose_graph->IsFinished(trajectory_id_)) {
      num_submaps_to_keep_ = 0;
  }
  // 实际调用 TrimmingHandle::GetSubmapIds
  auto submap_ids = pose_graph->GetSubmapIds(trajectory_id_);
  // 从序列号0开始裁剪子图，并删除相关的约束和节点
  // 剩下序列号大的子图
  for (std::size_t i = 0; i + num_submaps_to_keep_ < submap_ids.size(); ++i)
  {
      // 这是个大函数
      pose_graph->TrimSubmap(submap_ids.at(i)  );
  }
  if (num_submaps_to_keep_ == 0)
  {
      finished_ = true;
      pose_graph->SetTrajectoryState(
          trajectory_id_, 
          PoseGraphInterface::TrajectoryState::DELETED );
  }
}

1
2
3
4
5
6
7
8
9
10
11
12

std::vector<SubmapId> PoseGraph2D::TrimmingHandle::GetSubmapIds(
    int trajectory_id) const
{
  std::vector<SubmapId> submap_ids;
  // PoseGraph2D* const parent_;
  const auto& submap_data = parent_->optimization_problem_->submap_data();
  for (const auto& it : submap_data.trajectory(trajectory_id)  )
  {
      submap_ids.push_back(it.id);
  }
  return submap_ids;
}

核心是pose_graph->TrimSubmap，函数太长了，功能如下：

• 获取除submap_id外的所有子图的所有节点的id(nodes_to_retain)，这些节点是需要保留的
• 找到在submap.id的子图内部，同时不在别的子图内的节点(nodes_to.remove)，这些节点需要删除
• 删除submap_id相关的约束
• 删除与nodes_to_remove中节点相关联的约束，并对对应的submap_id进行标记
• 对标记的submap_id进行检查，看是否还存在其他子图间约束
• 删除没有子图间约束的标记的子图的扫描匹配器
• 删除submap_id这个子图的指针
• 删除submap_id这个子图的匹配器，与多分辨率地图
• 删除optimization_problem_中的submap_id这个子图
• 删除nodes_to_remove中的节点

纯定位时的匹配流程

PoseGraph2D::ComputeConstraint(node_id, submap_id) —— ConstraintBuilder2D::MaybeAddGlobalConstraint(submap_id, submap, node_id, constant_data) —— ConstraintBuilder2D::ComputeConstraint

第2步中

1
2
3
4

// 分别根据 node_id 和 submap_id 获得 节点数据和子图
const TrajectoryNode::Data* constant_data = data_.trajectory_nodes.at(node_id).constant_data.get();
const Submap2D* submap = static_cast<const Submap2D*>(data_.submap_data.at(submap_id).submap.get() );

第3步中，submap唯一的作用是获得初值：

1
2

const transform::Rigid2d initial_pose =
      ComputeSubmapPose(*submap) * initial_relative_pose;

cartographer的内容实在太庞大了，还有去除建图时动态障碍的模块。

在使用Cartographer建图时，存在环境中行人较多，或者建图时机器人周围人员一直跟随，导致最终建图后地图上存在行人噪点。

Cartographer在构建submap以及整体map时，实质是对栅格地图概率的更新，每一个node在栅格概率上的累加，可以去除建图时一般移动物体所产生的噪点。只要不是长时间停留在雷达探测范围内，栅格地图的概率会及时更新，最终生成的地图不会带有行人和车辆。但是实际建图中经常会出现多人跟在机器人周围建图或恰巧机器人旋转时周围人为移动，旋转时node快速生成，导致该部分submap中存在行人噪点，如果后期不重复走这条路径，最终生成的map会存在噪点，影响地图美观，以及路径规划是被视为障碍物。

cartographer在建图后比较每个栅格被击中和被路过的次数来判断动静态栅格。参数voxel_filter_and_remove_moving_objects和类OutlierRemovingPointsProcessor，可以用来配置Voxel过滤数据，并仅传递我们认为在非运动对象上的点。

追本溯源，发现这一机制只在cartographer_assets_writer中，顺序是 assets_writer_main.cc —— assets_writer.cc —— points_processor_pipeline_builder.cc中的RegisterBuiltInPointsProcessors —— OutlierRemovingPointsProcessor类

cartographer_assets_writer 使用.bag中的数据团和.pbstream中的轨迹. 配置文件可以用来上色，过滤，导出SLAM点云数据成不同的格式。

逻辑

其实很简单，有三个阶段，筛选出 hit > 0 的 voxel，计算经过这些voxel的 rays-cast 次数，可以按miss集合理解，然后比较rays和hits数目关系

1
2
3
4
5
6
7
8
9
10
11
12
13

// 第二阶段
// 如果栅格之前的 hit>0，那么就 ray 次数增加
if (voxels_.value(index).hits > 0)
{
  ++voxels_.mutable_value(index)->rays;
}

// 第三阶段
// 如果点的 rays > 3*hits 那么就认为是动态障碍物
if (!(voxel.rays < miss_per_hit_limit_ * voxel.hits))
{
    to_remove.insert(i);
}

运行

assets_writer_backup_2d.launch如下

1
2
3
4
5
6
7
8
9
10
11
12

<launch>
  <arg name="config_file" default="assets_writer_backpack_2d.lua"/>
  <node name="cartographer_assets_writer" pkg="cartographer_ros" required="true"
      type="cartographer_assets_writer" args="
          -configuration_directory $(find cartographer_ros)/configuration_files
          -configuration_basename $(arg config_file)
          -urdf_filename $(find cartographer_ros)/urdf/backpack_2d.urdf
          -bag_filenames $(arg bag_filenames)
          -pose_graph_filename $(arg pose_graph_filename)"
      output="screen">
  </node>
</launch>

参考：如何使用Cartographer生成的地图

—-title: SLAM中的图优化公式推导
date: 2022-09-20 22:17:51
categories:

- 算法推导

这里可以联系cartographer的前端理解。

以下为ubuntu18版本的g2o对应的代码，和16版不兼容。TEB的常见安装问题就是16版到18版不兼容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 求解器一般有两种, TEB用的是 Levenberg
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 3>> Block; // 每个误差项优化变量维度为3，误差值维度为1

Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();

Block* solver_ptr = new Block(std::unique_ptr<Block::LinearSolverType>(linearSolver) );

g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::unique_ptr<Block>(solver_ptr) );

g2o::SparseOptimizer optimizer;
// setAlgorithm()需要传递一个优化算法
optimizer.setAlgorithm(solver);
optimizer.setVerbose(true);
optimizer->initMultiThreading();

// ......
optimizer.optimize(maxIterations); 	//开始优化，设置迭代次数

• static bool initMultiThreading();

Eigen3.1开始，要求we call an initialize函数，如果从不同线程调用Eigen
如果g2o基于OpenMP编译，而且Eigen版本高于3.1，则这个函数调用 Eigen::initParallel

LinearSolver

它用来求解线性方程$H\Delta X = -b$ ，可以从PCG、CSparse、Choldmod、Dense、Eigen选择求解方法。

• LinearSolverCSparse：使用CSparse法。继承自LinearSolverCCS

• LinearSolverCholmod ：使用sparse cholesky分解法。继承自LinearSolverCCS

• LinearSolverDense ：使用dense cholesky分解法。继承自LinearSolver

• LinearSolverEigen： 依赖项只有eigen，使用eigen中的sparse Cholesky 求解，因此编译好后可以方便的在其他地方使用，性能和CSparse差不多。继承自LinearSolver

• LinearSolverPCG ：使用preconditioned conjugate gradient 法，继承自LinearSolver

选哪个求解器很重要，有一次使用LinearSolverDense，结果260秒才迭代一次，换成LinearSolverCSparse，0.4秒就迭代一次

TEB是涉及到CSparse和Choldmod，默认使用前者

解析器solver的另一种创建方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 加载几组 solver
G2O_USE_OPTIMIZATION_LIBRARY(pcg)
G2O_USE_OPTIMIZATION_LIBRARY(cholmod)
G2O_USE_OPTIMIZATION_LIBRARY(csparse)
G2O_USE_OPTIMIZATION_LIBRARY(dense)
G2O_USE_OPTIMIZATION_LIBRARY(eigen)


g2o::OptimizationAlgorithmFactory *solver_factory = g2o::OptimizationAlgorithmFactory::instance();
// 记录所有可用的 solver
std::ofstream fileout("/home/user/test_nodes/solvers.txt");
solver_factory->listSolvers(fileout);
// or lm_var_cparse
g2o::OptimizationAlgorithmProperty solver_property;
g2o::OptimizationAlgorithm *solver = solver_factory->construct("lm_var", solver_property);
std::unique_ptr<g2o::SparseOptimizer> optimizer(new g2o::SparseOptimizer());
optimizer->setAlgorithm(solver);

construct函数比上面的LinearSolverDense系列更灵活，设置求解器更精准。

使用listSolvers输出所有可用solver到文件，这个结果是和使用了多少G2O_USE_OPTIMIZATION_LIBRARY有关的，上面的5个应该涵盖了所有求解器，结果非常多。比如不加载G2O_USE_OPTIMIZATION_LIBRARY(eigen)，那么lm_var不可用，会报错 SOLVER FACTORY WARNING: Unable to create solver lm_var

listSolvers会输出所有求解器名称和解释，比如

1

lm_var    Eigen 	Levenberg: Cholesky solver using Eigen's Sparse Cholesky methods (variable blocksize)

优化结果

optimizer.setVerbose(true)后才能看到优化过程

或者g2o::SparseOptimizer::chi2()，优化前后各调用一次，可得到优化前后误差变化

1
2
3
4
5

iteration= 0	 chi2= 6973711.783675	 time= 0.228985	 cumTime= 0.228985	 edges= 3995	 schur= 0	 lambda= 42.450053	 levenbergIter= 1
iteration= 1	 chi2= 477444.019837	 time= 0.219176	 cumTime= 0.448161	 edges= 3995	 schur= 0	 lambda= 14.150018	 levenbergIter= 1
								......
iteration= 20	 chi2= 10344.665262	 time= 0.200148	 cumTime= 4.63974	 edges= 3995	 schur= 0	 lambda= 1.634041	 levenbergIter= 1
iteration= 21	 chi2= 10344.665262	 time= 0.461369	 cumTime= 5.10111	 edges= 3995	 schur= 0	 lambda= 112290463347.367386	 levenbergIter= 8

照搬其他人的讲解。

方程个数 > 未知数个数，也就是”超定”线性方程组。方程个数比未知数个数多，可以想象不同方程之间会出现”冲突”的现象，也就是说导致整个方程组没有精确解。但我们只要设定一个误差标准，找到一个让这个误差标准值最小的近似解也是完全可以接收的。即针对超定不相容线性方程组，利用最小二乘误差标准求解近似值。

1.1 首先构建位姿之间的关系，即图的边

下面和开头的非线性最小二乘的推导一样了

问题：用最小二乘拟合直线，什么时候会失败？

答: 矩阵 $A^TA$ 不可逆的情况。 我的理解是把最小二乘按正规方程解法，也就是先获得 $A^TAx = A^Tb$，这是一个 n×n
的线性方程组，称为正规方程组。显然解为 $x = (A^TA)^{-1}A^Tb$

图优化SLAM通过减去原始传感器的测量，构建了简化的估计问题。这些原始的测量由图中的边取代，边可以看做“虚拟测量”(virtual measurements)。图中的两个节点之间的边是用两个位姿之间的相对位置的概率分布表示的，这一概率分布的条件是它们的相互测量。观测模型 $p(z_t | \ x_t, m_t)$ 是多模态的，因此高斯分布的假设不成立。这意味着一次观测 $z_t$ 可能影响图中连接不同位姿的多条边。 graph connectivity 应当用概率分布来描述。如果直接处理这个多模态问题，将出现极大的复杂度。我们需要将地图变成node和edge的拓扑结构。因此，需要确定不同node之间的edge约束。

我们应当判断一次观测导致的最可能约束，这取决于机器人位姿的概率分布。这一问题称作data association，常由SLAM后端解决。前端需要对机器人轨迹 $p(X_{1:T} \ | \ Z_{1:T}, \ u_{1:T})$ 上的条件先验进行一致估计，这就要求机器人运动过程中对前端和后端穿插地执行。因此后端的准确性和效率对SLAM系统非常重要。

如果观测值受局部高斯噪声影响，而且data association已知，基于图的建图算法的目标就是机器人轨迹的高斯估计后验。包括计算这个高斯分布的均值，然后以均值作为节点的configuration，这样最大化了观测的似然。

• 图优化中，顶点是优化项，而边是约束项。优化过程就是通过全局调整优化项，使约束项的和最小。
• Pose(x)与Landmark(m)构成了图的顶点集
• 边(Edge)存在两种。第一种是Pose到Pose，另一种是Pose到 Landmark

• 图优化中边表示约束，Pose到Pose的边与机器人的运动模型相关，机器人从$x_0$运动到$x_1$，形成了这条边。同时在运动模型的作用下，可以获得机器人在$x_0$，控制量为$u_1$时的状态 g。该值与“真实”的Pose 的差，构成了这条边的约束。由于边的约束是标量，因此取这个差的平方。R表示为运动模型的协方差。公式可以写作 $(x_1 - g)^T R^{-1}(x_1 - g)$

• Pose到Landmark的边与机器人的观测模型相关，机器人从 $x_{1}$观测到 $m_{1}$，就会形成一条边。同时在观测模型 $h_{(measure, Pose)}$ 的作用下，可以获得机器人在 $x_{1}$ 时对 $m_1$ 的预测 $h_{(m_{1}, x_{1})}$。该值与此时真正观测到的值 $z_{1}$ 的差，构成了这条边的约束。同样的，取这个差的平方作为约束值。$Q$ 表示为观测模型的协方差。公式 $[z_1 - h(m_1,x_1)]^TQ^{-1}[z_1 - h(m_1,x_1)]$

• 完整的约束为两种约束的和 $J_{GraghSLAM}$

SLAM的图优化问题就是寻找合适的 Pose(x), Landmark(m)，使 $J_{GraghSLAM}$ 最小。

看到预测值和观测值的差，很容易想到Cartographer，PoseExtrapolator提供预测值，Scan Matcher提供观测值。

或者可以这样理解：


我们用$e(x_i,x_j,z_{ij})$ 表示预测值和观测值之间的差，假设其满足高斯分布 $N(0, \Sigma)$，或者说观测值的分布是以真值为中心的多元高斯分布。 我们的目标是让预测值和观测值尽可能趋近于0（均值），也就是让 $e$ 出现在概率最大的地方，这就是个最大似然的问题。 我们让概率密度函数取最大值

把图中的x换成 $e(x_i,x_j,z_{ij})$， 均值取0，得到下面的最小二乘形式

最小二乘问题的目标函数的变量维度很高，但每个误差项都是简单的，仅与少量变量有关。因此为了直观的展示变量与变量之间的关系，可以把优化问题用图的方式来展现。其中顶点表示优化变量，边表示误差项。

图优化的流程

1. 选择你想要的图里的顶点与边的类型，确定它们的参数化形式

2. 往图里加入实际的顶点和边

3. 选择初值，开始迭代

4. 每一步迭代中，计算对应于当前估计值的雅可比矩阵和海塞矩阵

5. 求解稀疏线性方程 $H_k \Delta x = -b_k$ ，得到梯度方向

6. 继续用高斯牛顿法(GN)或列文列文伯格-马夸尔特法(LM)进行迭代。如果迭代结束，返回优化值。

SLAM中的图优化

滤波类算法最大的问题，是无法处理大尺度场景的建图。由于滤波类算法是基于递归计算的，下一时刻的估计值依赖于上一时刻的估计，因而在大尺度场景下，由于系统参数和传感器观测数据的不准确性，会造成误差慢慢累积，一旦当前时刻的估计出现偏差，无法修正该误差，最终无法获得一致性的地图。

另外滤波方法对计算量和内存消耗都很大，使用图优化方法则效率较高，这种方法位姿不是实时纠正，而是将数据记录下来，最后进行计算优化。

机器人的位姿是一个顶点(vertex)，位姿之间的关系构成边(edge)，边表示两个位姿的空间约束(相对位姿和对应方差)。比如t+1时刻和t时刻之间的里程计关系构成边，或者由视觉计算出来的位姿转换矩阵也可以构成边。图构建完成后，就要调整机器人的位姿去尽量满足这些边构成的约束。图优化就是构建图并调整各顶点的位姿，使预测和观测的误差最小。每一条边的信息矩阵就是协方差矩阵的逆。协方差越小，说明这次测量越准，信息权重就越大。

前端： 从里程计和激光雷达数据中求得位姿，构建图。机器人位姿当做顶点，位姿间关系当做边，常常是传感器信息的堆积
后端： 在图构建好以后，采用回环检测，出现了回环边说明有误差。构造闭环约束，调整机器人位姿，通过最小化观测和估计残差求得优化后的位姿。

通过帧间匹配得到 $X_8$ 和 $X_2$之间的相对位姿，称为观测值

观测方程也有很多形式，如：

• 机器人两个Pose之间的变换；
• 机器人在某个Pose处用激光测量到了某个空间点，得到了它离自己的距离与角度；
• 机器人在某个Pose处用相机观测到了某个空间点，得到了它的像素坐标；

同样，它们的具体形式很多样化，这允许我们在讨论slam问题时，不局限于某种特定的传感器或姿态表达方式。

这个减法只是通用的，在SLAM里可能没有定义减法。