参考这位博主的文章,工程optimized_ICP,看完这位大姐写的,再去看ALOAM,感觉容易理解了很多。ALOAM就是两种特征点的ICP匹配,比本例稍复杂,改用ceres优化(张楫是手推的雅格比)
- 对原始点云,给定初值T,使用
pcl::transformPointCloud获得变换后的待匹配点云。 - 在目标点云中,
nearestKSearch搜索距离待匹配点云最近的一个点,记录下此点的索引和二者之间的距离的平方resultant_distances - 判断
resultant_distances和参数max_correspond_distance_的大小,大于则continue - 找出了待匹配点云和目标点云对应的一对点,也就是取最近点作为关联点,求它们的差值
error
目标函数
i 为通过最近邻搜索匹配上的点对, 和 分别为目标点云和待匹配点云中的点
R, t 分别为两个点云之间的旋转和平移变换。目标函数对R和t求导,文章写的是左扰动模型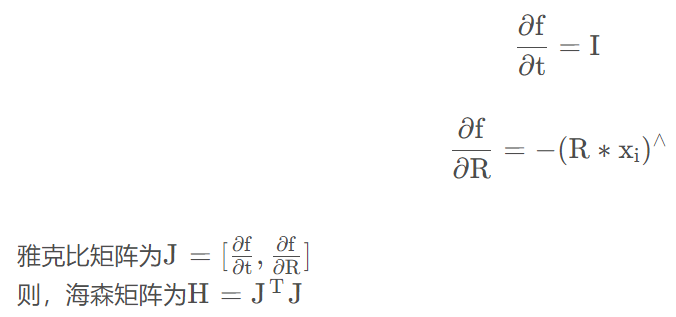
但是代码里用的是右扰动模型
最终的求 的方程还是我们熟悉的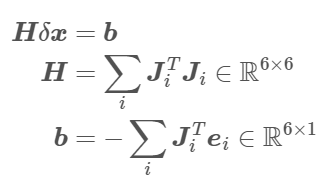
1 | for() |
