照搬其他人的讲解。

方程个数 > 未知数个数，也就是”超定”线性方程组。方程个数比未知数个数多，可以想象不同方程之间会出现”冲突”的现象，也就是说导致整个方程组没有精确解。但我们只要设定一个误差标准，找到一个让这个误差标准值最小的近似解也是完全可以接收的。即针对超定不相容线性方程组，利用最小二乘误差标准求解近似值。

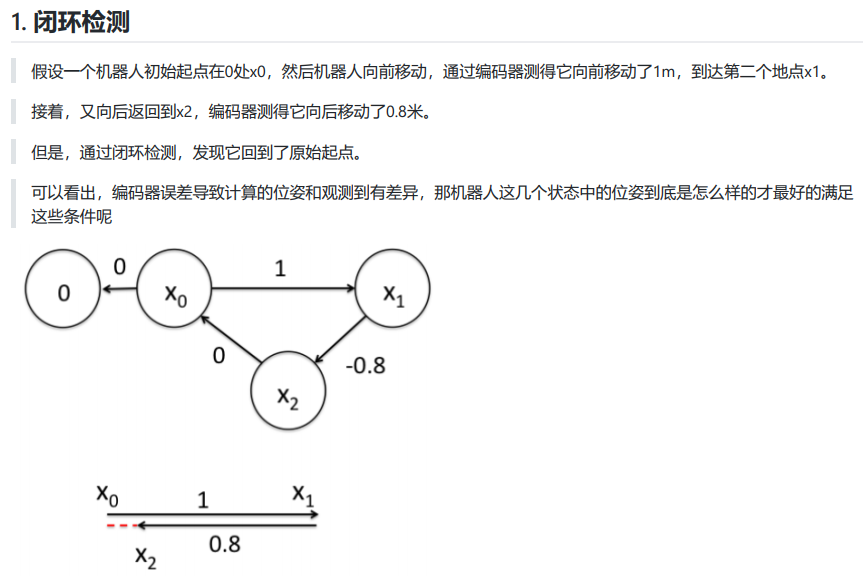
1.1 首先构建位姿之间的关系，即图的边

下面和开头的非线性最小二乘的推导一样了

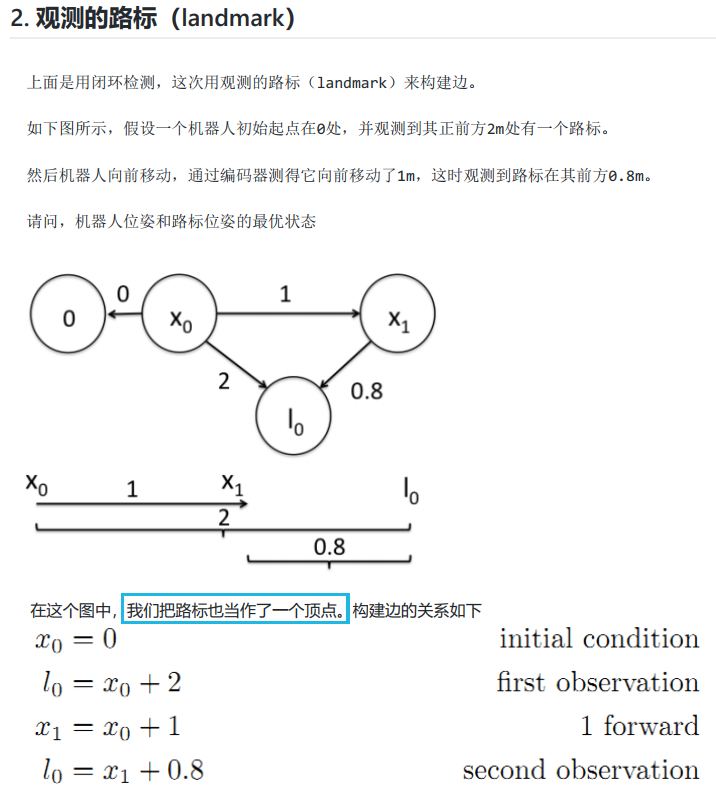
问题：用最小二乘拟合直线，什么时候会失败？

答: 矩阵 $A^TA$ 不可逆的情况。 我的理解是把最小二乘按正规方程解法，也就是先获得 $A^TAx = A^Tb$，这是一个 n×n
的线性方程组，称为正规方程组。显然解为 $x = (A^TA)^{-1}A^Tb$