旋转

有旋转向量、四元数和旋转矩阵三种表示方法，在Eigen里用前两种进行定义，这样参数少，可以转化为第三种。

牢记下面这张图，根据《视觉SLAM十四讲》总结：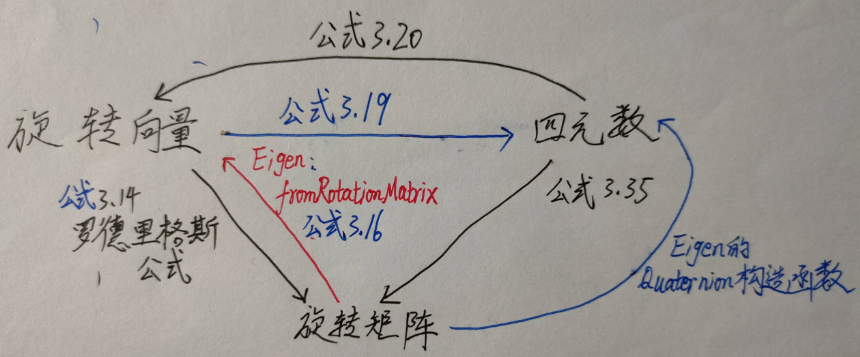

使用的是模板类：class Eigen::AngleAxis< Scalar >，这被称为角轴表示法，顾名思义给定旋转角度和旋转轴即可。其创建方式符合Eigen的原则，传入数据类型作为模板参数。旋转角度以弧度表示，旋转轴为Vector类型的向量，注意向量必须要被归一化(vec.normalized()即可)。Eigen中也预先定义好了AngleAxisd和AngleAxisf两种方便使用。

参考:基于eigen实现欧拉角(RPY), 旋转矩阵, 旋转向量, 四元数之间的变换

Vector3f v1 = Vector3f::UnitX();

AngleAxisf aa(45*3.1415/180, v1);
// 返回弧度制表示的旋转角度 和 旋转轴(列向量)
cout << aa.angle() <<"  "<<endl<< aa.axis() <<endl; 
cout << aa.toRotationMatrix()<<endl;   // 转换为3 × 3的旋转矩阵

// fromRotationMatrix():从一个3×3的旋转矩阵构建AngleAxis对象。也就是提取旋转矩阵所表示的旋转角
//  inverse(): 返回以AngleAxis表示的当前旋转的逆旋转

Quaternion是四元数表示法，Quaternion的构造是标准Eigen格式：数据类型作为模板参数+构造参数，而且重载了多个构造函数，因此可以方便地从角轴、旋转矩阵等数据类型进行构造。

Eigen提供了Quaternionf和Quaterniond方便使用。Quaterniond的初始化：

Eigen::Quaterniond q1(x, y, z, w);
 
Eigen::Quaterniond q2(Vector4d(x, y, z, w));
 
Eigen::Quaterniond q2(Matrix3d(R));

在Quaternion内部的保存中，虚部在前，实部在后。

如果以第一种方式构造四元数，则实部是x，虚部是[y,z,w]。 对于第二种方式，则实部是w，虚部是[x,y,z]； 对于第三种方式，则是用3x3的旋转矩阵初始化四元数。

所以最常用是 Eigen::Quaterniond q1(w, x, y, z); ，四个数的传入顺序是w、x、y、z，对应w+xi+yj+zk。

Eigen::Quaterniond 不能使用cout

• Identity(): 返回一个表示单位旋转的四元数

• w(): 返回四元数中的w分量。 同理 x(), y(), z()是返回相应的分量。

• coeffs(): 返回四元数的四个数，可以对其进行索引[]获取值。 需要注意的是返回顺序是x、y、z、w，和构造函数的不同

• toRotationMatrix() 将当前Quaternion对象转换为3×3的旋转矩阵。另外，没有fromRotationMatrix()函数，只能用构造函数传入旋转矩阵

• slerp():对两个四元数进行球面线性插值(Spherical linear interpolation，通常简称Slerp)，是四元数的一种线性插值运算，主要用于在两个表示旋转的四元数之间平滑差值。

欧拉角 —— 旋转矩阵

可以让三个AngleAxis相乘：

// 参数顺序和 static_transform_publisher 的一致
Eigen::Vector3f angle(roll, pitch, yaw);
Eigen::Matrix3d rotation;
rotation = Eigen::AngleAxisd(angle[0], Eigen::Vector3d::UnitZ()) *
           Eigen::AngleAxisd(angle[1], Eigen::Vector3d::UnitY()) *
           Eigen::AngleAxisd(angle[2], Eigen::Vector3d::UnitX()) ;

这样计算的结果和每个AngleAxisf转换成旋转矩阵后再相乘得到的结果是相同的

旋转矩阵转欧拉角的结果可能不是想要的，最好不使用

四元数 —— 旋转矩阵

其实这样更简单，我们可以直接从tf2_ros::Buffer和geometry_msgs::TransformStamped直接获得四元数

Eigen::Quaterniond quaternion(transform.transform.rotation.w,
                              transform.transform.rotation.x,
                              transform.transform.rotation.y,
                              transform.transform.rotation.z
                              );
Eigen::Matrix3d rotation = quaternion.matrix();

平移

采用Eigen标准构造原则，构造示例如下：

Translation<float,2>(tx, ty)
Translation<float,3>(tx, ty, tz)
Translation<float,N>(s)
Translation<float,N>(vecN)

多个平移合并用乘号而不是加号，需要注意。和旋转相比，它的成员函数也相对少一些:

• x():获取平移的x分量(可修改)

• y():获取平移的y分量(可修改)

• z():获取平移的z分量(可修改)，注意，千万不要对一个二维的Translation获取z分量，否则直接会运行报错

• vector()&.translation():返回当前平移的向量表示(可修改)，可以索引[]获取各分量

Translation2d t1(1,4);
Translation2d t2(2,7);
Translation2d t3;
t3=t1*t2;
cout<<t3.translation()<<endl;

计算特征值与特征向量

构造一个EigenSolver，然后分别调用其成员函数.eigenvalues()、.eigenvectors()即可获得特征值与特征向量。

#include <Eigen/Eigenvalues>

A << 2,-2,0, -2,1,-2, 0,-2,0;
EigenSolver<Matrix3d> eigensolver(A);
if (eigensolver.info() == Success)
{
    cout << eigensolver.eigenvalues() << endl<<endl;
    cout << eigensolver.eigenvectors() << endl;
}

输出结果并不是我们平时熟悉的形式，而是

(4,0)
(1,0)
(-2,0)

(-0.666667,0) (-0.666667,0) (-0.333333,0)
(0.666667,0) (-0.333333,0) (-0.666667,0)
(-0.333333,0)  (0.666667,0) (-0.666667,0)

实际特征值是4,1,-2. 4对应的特征向量分别为(-0.666667, -0.666667,-0.333333)

参考：
C++ Eigen库计算矩阵特征值及特征向量
Eigen函数与Matlab对应关系