插值指在离散数据的基础上补插连续函数，使得连续曲线 通过全部给定的离散数据点。 插值的本质 —— 利用已知数据估计未知位置数值。插值和拟合的不同之处在于：对于给定的函数，插值 要求离散点“坐落在”函数曲线上从而满足约束；而 拟合 则希望离散点尽可能地 “逼近” 函数曲线。

双线性插值 Bilinear Interpolation

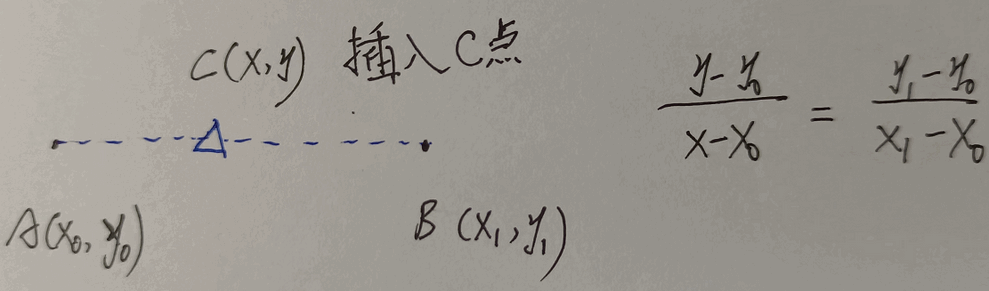
普通的线性插值我们都很熟悉。 双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。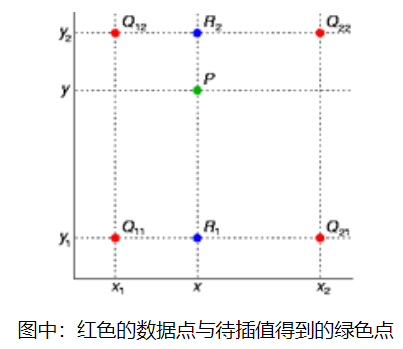


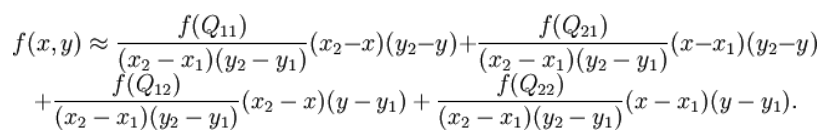
看这个推导

双线性插值在三维空间的延伸是三线性插值。

双三次插值 Bicubic interpolation

二维空间中最常用的插值方法。在这种方法中，函数f在点(x , y)的值可以通过矩形网格中最近的十六个采样点的加权平均得到，在这里需要使用两个多项式插值三次函数，每个方向使用一个。

双三次插值通过下式进行计算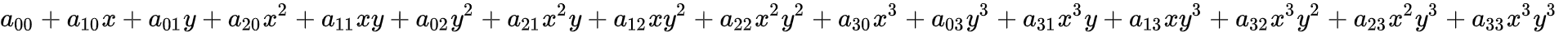

$$\mathop{\Sigma}\limits_{i=0}\limits^{3} \mathop{\Sigma}\limits_{j=0}\limits^{3} a_{ij}x^iy^j$$

计算系数的过程依赖于插值数据的特性。如果已知插值函数的导数，常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数与表示x与y方向的表面斜率，二阶相互导数表示同时在x与y方向的斜率。这些值可以通过分别连续对x与y向量取微分得到。对于网格单元的每个顶点，将局部坐标(0,0), (1,0), (0,1)和(1,1)带入这些方程，再解这16个方程