choskey分解

Cholesky分解一个重要的应用就是解方程组 Ax = B，其中A是一个正定矩阵。因为A是一个正定矩阵，所以有A =LL^T，其中L是一个下三角矩阵。原方程组可以写成 LL^Tx = B。如果令 y = L^Tx ，则有Ly = B。注意到L是一个下三角矩阵，所以从下向上求解y是非常容易的. 求解出y之后，在按照类似的方法求解y = L^Tx 中的 x，而其中L^T是一个上三角矩阵，所以最终求出 x 也是非常容易的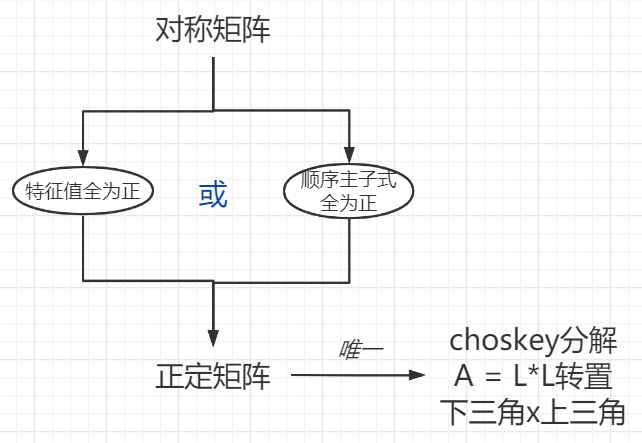

cholesky分解又称为平方根法，是A为实对称正定矩阵时，LU分解的变形。

协方差矩阵是实对称半正定的，如果对角线元素全为正，则可进行cholesky分解， $\Sigma = LL^T$

计算样本中两个特征向量的距离，可以用马氏距离表示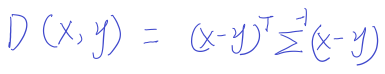

直接对协方差求逆比较复杂，使用cholesky分解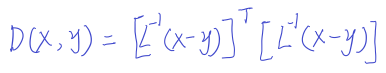

LDLT

LDLT分解法实际上是Cholesky分解法的改进， 优先使用LDLT而不是LLT方法。 Cholesky分解法虽然不需要选主元，但其运算过程中涉及到开方问题，而LDLT分解法则避免了这一问题。 若对称矩阵A的各阶顺序主子式不为零时，则A可以唯一分解为 $A=LDL^T$ 。 其中 L 为下三角单位矩阵 (即主对角线元素皆为 1，下三角其他元素不为0)，D为对角矩阵，$L^T$ 为L的转置矩阵。

LDLT则可以应对半正定和负半定问题，精度较LLT更高

QR分解

对于任意的实数矩阵 $A\in C^{n\times n}$，存在 n阶正交矩阵 Q 和 n阶上三角矩阵 R，使得 $A=Q*R$。注意：矩阵A可以是非方阵。 正交矩阵： $Q^{-1}=Q^T$

如果A是非奇异的，且限定R的对角线元素为正，则这个分解是唯一的。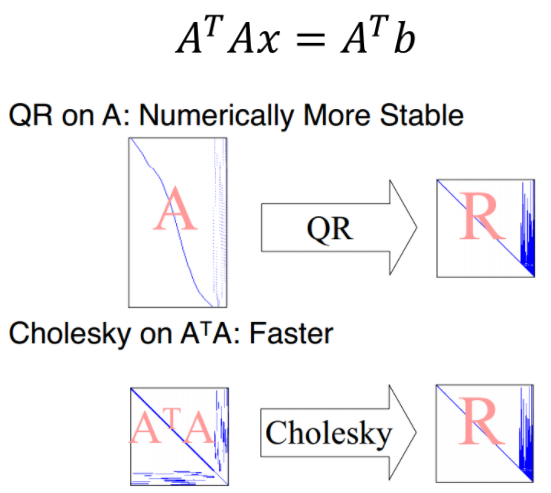

实际计算有Givens旋转、Householder变换，以及Gram-Schmidt正交化等。Eigen常用的是 Householder变换

用于求线性方程组

对于直接求解线性方程组的逆，用QR分解的方法求解会更具有数据的稳定性。 对于求解一个线性系统Ax = b, 这里A的维度是 m x n。

上三角矩阵R的逆矩阵仍然是上三角矩阵，可以用分块矩阵迭代的方法很容易地求出来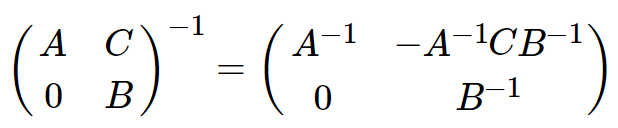

下三角矩阵的逆矩阵也是类似求法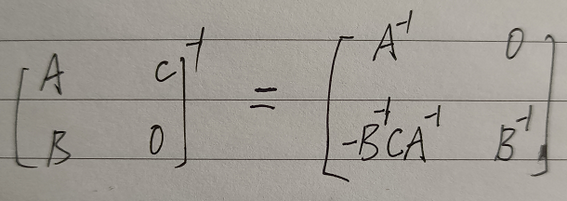

SVD分解 - 奇异值分解

特征值分解仅针对方阵，而不是方阵的矩阵就有了SVD分解： $A=U\Sigma V^T$

其中A为m x n的矩阵， 正交矩阵 U(m x m阶) 和 V(n x n阶)。

$$\Sigma_{mn} = \left[ \begin{matrix} \Sigma_1 & 0 \\ 0 & 0 \\ \end{matrix} \right]$$ $$\Sigma_1=diag(\sigma_1....\sigma_r)$$

其中 $\sigma_i$ 是矩阵 $\Sigma_{1}$ 的特征值

矩阵U的列称为左奇异向量，是正交的。 矩阵V的列向量(也称为右奇异向量)也是正交的.

此时的A如果是方阵，那么逆矩阵也很容易求出: $A^{-1} = V\Sigma^{-1}U^T$

奇异值分解同时包含了旋转、缩放($\Sigma$)和投影三种作用。特征值分解只有缩放的效果。