沉默杀手HomeArchivesTagsCategories
欧拉角和四元数
|ROSROS Kinetic知识|
Word count: 697|Reading time: 2 min

概念

欧拉角其实就是表示向三个方向旋转的角度，比较形象直观。四元数是等价的另一种表示方法，不能直观体现，但是具备一些优点。数学理论实在太复杂，只需要记住以下几条：

  • 欧拉角就是绕Z轴、Y轴、X轴的旋转角度，记做ψ、θ、φ，分别为Yaw（偏航）、Pitch（俯仰）、Roll（翻滚）
  • 四元数是w,x,y,z，它们的平方和是1
  • 欧拉角会出现万向节死锁，比如三维空间中有一个平行于 X 轴的向量，将它绕 Y 轴旋转直到它平行于 Z 轴，这时任何绕 Z 轴的旋转都改变不了该向量的方向

三个旋转方向如图所示：

欧拉角到四元数的转换: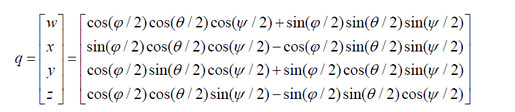

四元数到欧拉角的转换:

描述机器人转弯的角就是绕Z轴的旋转，按照右手法则可以知道机器人向左转为正，右转为负。

ROS中的欧拉角 四元数

geometry_msgs/Quaternion消息

1
2
3
4
float64 x
float64 y
float64 z
float64 w

geometry_msgs/Transform消息

1
2
geometry_msgs/Vector3 translation
geometry_msgs/Quaternion rotation

这两个各自有一个加时间戳的消息类型。


除了geometry_msgs/Quaternion，还有一个tf::Quaternion类，重要函数：

1
2
3
4
5
Vector3  getAxis () const    //Return the axis of the rotation represented by this quaternion. 
//Set the quaternion using fixed axis RPY. 
void 	setRPY (const tfScalar &roll, const tfScalar &pitch, const tfScalar &yaw)    
//Return an identity quaternion.
tf::Quaternion createIdentityQuaternion()

还有一个有点特殊的函数，直接返回yaw，但是范围是[0, 2Pi]，所以尽量不要使用

1
tf::Quaternion::getAngle () const

geometry_msgs::Quaternion —— tf::Quaternion 转换如下 
1
2
// [inline, static]
static void tf::quaternionMsgToTF(const geometry_msgs::Quaternion& msg, tf::Quaternion& bt)

四元数——欧拉角

1
2
3
4
tf::Quaternion quat;
double roll, pitch, yaw;
// 赋值给quat，getRPY函数 将quat转为欧拉角
tf::Matrix3x3(quat).getRPY(roll, pitch, yaw);

orientation是表示朝向的消息成员，也就是四元数，类型const geometry_msgs::Quaternion &。 常常配合tf::quaternionMsgToTF函数使用，因为我们一般是先获得geometry_msgs::Quaternion类型

或者用tf2的方式

1
2
3
4
5
6
7
#include “tf2/LinearMath/Matrix3x3.h”

tf2::Matrix3x3 mat(tf2::Quaternion( x, y, z, w) );
mat.getEulerYPR(tf2Scalar&  yaw,
tf2Scalar&  pitch,
tf2Scalar& 	roll,
unsigned int 	solution_number = 1);

欧拉角 —— 四元数

1
2
3
4
5
6
7
8
9
//只通过yaw计算四元数，用于平面小车
static geometry_msgs::Quaternion  tf::createQuaternionMsgFromYaw(double yaw);

static tf::Quaternion  createQuaternionFromYaw (double yaw)

static tf::Quaternion  createQuaternionFromRPY(double roll, double pitch, double yaw)

static geometry_msgs::Quaternion  createQuaternionMsgFromRollPitchYaw( double roll, 
	double pitch,   double yaw)

python常见的写法:

1
2
3
pos = Pose()
q = tf.transformations.quaternion_from_euler(0, 0, point.z)
pos.orientation = q

但是经测试，这样写是有问题的，正确的写法如下：
1
2
3
4
5
6
pos = Pose()
q = tf.transformations.quaternion_from_euler(0, 0, point.z)
pos.orientation.x = q[0]
pos.orientation.y = q[1]
pos.orientation.z = q[2]
pos.orientation.w = q[3]

报错积累

报错 MSG to TF: Quaternion Not Properly Normalized ， 原因是接受的位姿的四元数不合理。

参考：
四元数与欧拉角（Yaw、Pitch、Roll）的转换