沉默杀手HomeArchivesTagsCategories
(十一) optimizeTEB 2 初始化g2o求解器和添加约束
|路径规划TEB算法|
Word count: 1.5k|Reading time: 6 min

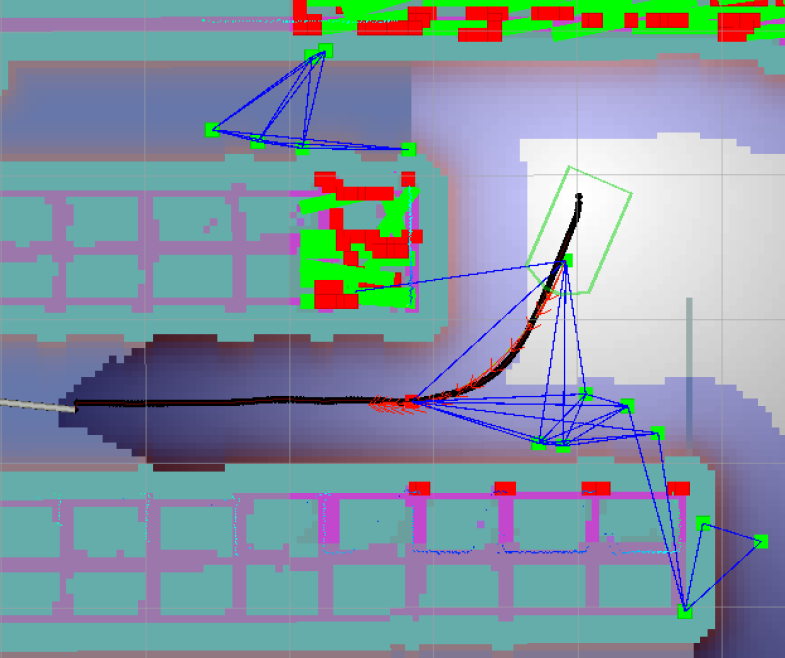
g2o边和顶点的定义

所有边都在头文件base_teb_edges.h中，顶点就是g2o_types\vertex_timediff.h 和 g2o_types\vertex_pose.h。两个顶点都比较简单，值得注意的是vertex_timediff.h的setToOriginImpl

1
2
3
4
virtual void setToOriginImpl()
{
  _estimate = 0.1;  // 不是0，不明白为什么
}

一元边：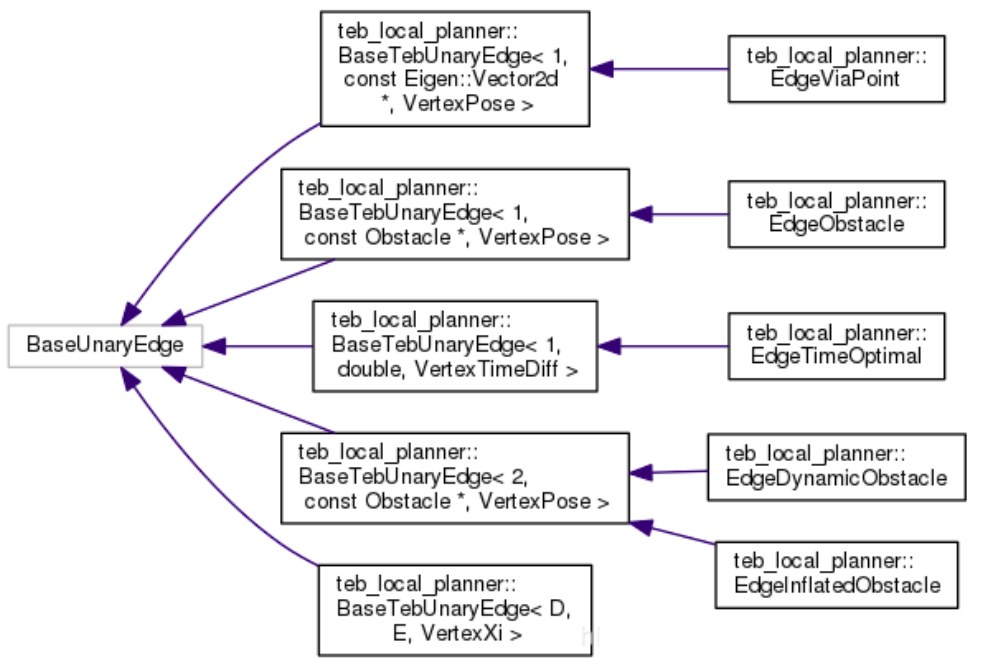

1
2
template <int D, typename E, typename VertexXi>
class BaseTebUnaryEdge : public g2o::BaseUnaryEdge<D, E, VertexXi>

  • EdgeViaPoint：以指定的经过点位置与待优化位姿（顶点）的误差作为目标。（保证轨迹会经过指定点）

  • EdgeObstacle：以障碍物与待优化位姿（顶点）的距离经过惩罚函数后的输出作为目标（保证离障碍物大于一定距离）

  • EdgeTimeOptimal：以时间间隔dt最小作为目标（保证时间最短轨迹）

二元边
二元边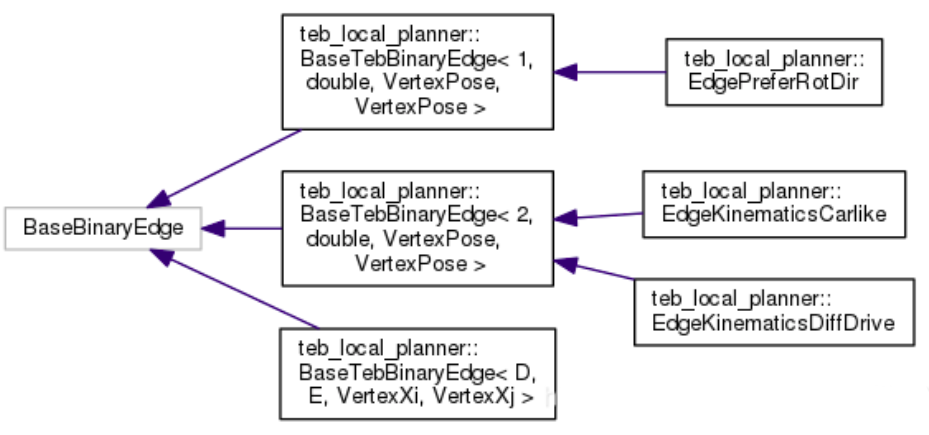

1
2
template <int D, typename E, typename VertexXi, typename VertexXj>
class BaseTebBinaryEdge : public g2o::BaseBinaryEdge<D, E, VertexXi, VertexXj>

主要是考虑了运动学的约束关系（车的相邻的两个位姿态必须落在一个圆弧上）。二元边的两个顶点分别是两个位姿，还限制了最小转弯半径。

多元边（构造函数中resize顶点的个数）：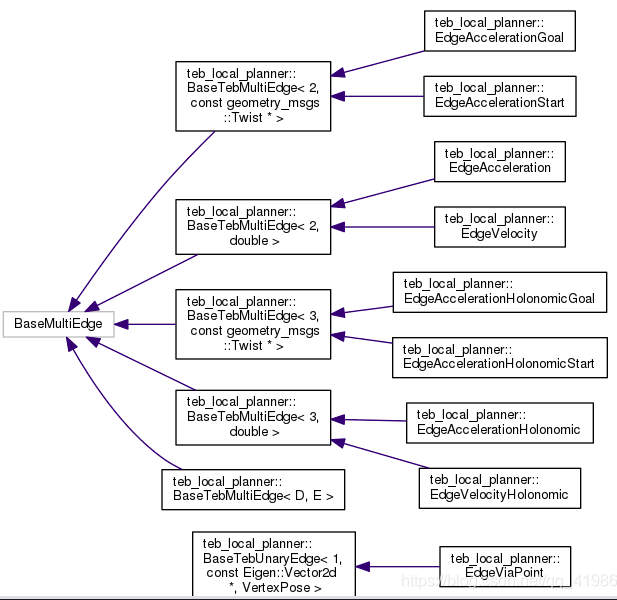

1
2
template <int D, typename E>
class BaseTebMultiEdge : public g2o::BaseMultiEdge<D, E>

  • EdgeVelocity：以实际速度和限定最大速度经过惩罚函数的输出作为目标函数，顶点为相邻的位姿和时间间隔。（限制实际速度不超过最大，程序中引入了sigmoid函数决定速度的符号（根据论文内的说法，引入此函数是因为优化算法只能求解连续函数）

  • Edgevelocityholonomic：与EdgeVelocity的区别在于，ds是机器人本体坐标系下的，然后去求速度在本体坐标系下的表示。其余思路一致


1
2
3
class VertexPose : public g2o::BaseVertex<3, PoseSE2 >

class VertexTimeDiff : public g2o::BaseVertex<1, double>

初始化 optimizer

planner_初始化在if (cfg_.hcp.enable_homotopy_class_planning)的判断里，然后实际调用TebOptimalPlanner::initialize或者HomotopyClassPlanner::initialize，前者调用了TebOptimalPlanner::initOptimizer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
boost::shared_ptr<g2o::SparseOptimizer> TebOptimalPlanner::initOptimizer()
{
    // Call register_g2o_types once, even for multiple TebOptimalPlanner instances (thread-safe)
    static boost::once_flag flag = BOOST_ONCE_INIT;
    // 将为TEB定义的顶点和边注册到g2o::Factory
    boost::call_once(&registerG2OTypes, flag);  

    // allocating the optimizer
    boost::shared_ptr<g2o::SparseOptimizer> optimizer = boost::make_shared<g2o::SparseOptimizer>();
    //        linear solver utilized for optimization
    // 针对稀疏矩阵，写死为 g2o::LinearSolverCSparse
    // typedef  g2o::LinearSolverCSparse<TEBBlockSolver::PoseMatrixType> TEBLinearSolver;
    TEBLinearSolver* linearSolver = new TEBLinearSolver(); // see typedef in optimization.h
    linearSolver->setBlockOrdering(true);

    //      block  solver utilized for optimization
    // typedef   g2o::BlockSolver< g2o::BlockSolverTraits<-1, -1> >  TEBBlockSolver;
    TEBBlockSolver* blockSolver = new TEBBlockSolver(linearSolver);
    g2o::OptimizationAlgorithmLevenberg* solver = 
                new g2o::OptimizationAlgorithmLevenberg(blockSolver);

    optimizer->setAlgorithm(solver);
    optimizer->initMultiThreading(); // required for >Eigen 3.1

    return optimizer;
}

注意算法求解器写死为 利文伯格法 和 g2o::LinearSolverCSparse


构建超图 buildGraph

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
bool TebOptimalPlanner::buildGraph(double weight_multiplier)
{
  // 构建图优化问题。若顶点和边非空，则 add
  if (!optimizer_->edges().empty() || !optimizer_->vertices().empty())
  {
    ROS_WARN("Cannot build graph, because it is not empty. Call graphClear() ");
    return false;
  }
  // 增加图的顶点，TimedElasticBand类型的路径点和dt为顶点
  // 添加顺序会影响 稀疏矩阵的结构，进而影响优化效率
  AddTEBVertices();
  // add Edges (local cost functions)
  // legacy_obstacle_association 
  /*已经修改了将轨迹姿势与优化障碍联系起来的策略（参见changelog）。 
    您可以通过将此参数设置为true来切换到 旧策略。 
     旧策略：对于每个障碍，找到最近的TEB姿势; 新策略：对于每个teb姿势，只找到“相关”的障碍  */
  if (cfg_->obstacles.legacy_obstacle_association)   // false
      AddEdgesObstaclesLegacy(weight_multiplier);
  else
      AddEdgesObstacles(weight_multiplier);   // 参数写死为 2

  if (cfg_->obstacles.include_dynamic_obstacles)
      AddEdgesDynamicObstacles();
   /* error为其连接的Pose顶点的位置到这个Viapoint的距离的模长。
     信息矩阵为1x1的矩阵，其值为 weight_viapoint
     添加全局路径约束, 取决于参数 global_plan_viapoint_sep */
  AddEdgesViaPoints();

  // 对于TimedElasticBand类型中的位姿顶点序列-1条边，设置该边的顶点和权重矩阵，添加该边
  AddEdgesVelocity();
  AddEdgesAcceleration();
  AddEdgesJerk();   // 实际不执行
  // error直接就是连接的VertexTimeDiff的dt本身,信息矩阵为1x1矩阵，其值为weight_optimaltime
  AddEdgesTimeOptimal();   //添加时间约束
  
  if (cfg_->robot.min_turning_radius == 0 || cfg_->optim.weight_kinematics_turning_radius == 0)
    AddEdgesKinematicsDiffDrive(); // differential drive robot
  else
    AddEdgesKinematicsCarlike(); // carlike robot since the turning radius is bounded from below.

  AddEdgesPreferRotDir();   // 实际不执行
  return true;  
}

添加 vertex

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void TebOptimalPlanner::AddTEBVertices()
{
  // add vertices to graph
  ROS_DEBUG_COND(cfg_->optim.optimization_verbose, "Adding TEB vertices ...");
  unsigned int id_counter = 0; // used for vertices ids
  // std::vector<ObstContainer> obstacles_per_vertex_; 对应n-1 initial vertices
  obstacles_per_vertex_.resize(teb_.sizePoses());
  auto iter_obstacle = obstacles_per_vertex_.begin();
  for (int i=0; i < teb_.sizePoses(); ++i)
  {
      // 两种 vertex 都要添加
      teb_.PoseVertex(i)->setId(id_counter++);
      optimizer_->addVertex(teb_.PoseVertex(i) );
      if (teb_.sizeTimeDiffs()!=0 && i<teb_.sizeTimeDiffs() )
      {
          teb_.TimeDiffVertex(i)->setId(id_counter++);
          optimizer_->addVertex(teb_.TimeDiffVertex(i) );
      }
      iter_obstacle->clear();
      // 这里和 AddEdgesObstacles 有关
      (iter_obstacle++)->reserve( obstacles_->size()  );
  }
}

这里的Vertex没有调用setEstimate函数，不设置初值。

添加约束

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void TebOptimalPlanner::AddEdgesVelocity()
{
  // 只看 non-holonomic robot
    if ( cfg_->optim.weight_max_vel_x==0 && cfg_->optim.weight_max_vel_theta==0)
        return;

    int n = teb_.sizePoses();
    Eigen::Matrix<double,2,2> information;
    // 对角线元素
    information(0,0) = cfg_->optim.weight_max_vel_x;
    information(1,1) = cfg_->optim.weight_max_vel_theta;
    information(0,1) = 0.0;
    information(1,0) = 0.0;
    // 对所有的位姿，信息矩阵都是相同的
    for (int i=0; i < n - 1; ++i)
    {
      EdgeVelocity* velocity_edge = new EdgeVelocity;
      // 速度约束有三个顶点， 多元边
      velocity_edge->setVertex(0,teb_.PoseVertex(i));
      velocity_edge->setVertex(1,teb_.PoseVertex(i+1));
      velocity_edge->setVertex(2,teb_.TimeDiffVertex(i));

      velocity_edge->setInformation(information);
      velocity_edge->setTebConfig(*cfg_);
      optimizer_->addEdge(velocity_edge);
    }
}

error有两项，分别是线速度与线速度线速度是否在设定好的区间内。

只要看懂了论文和g2o的应用套路，这里的添加的edge大部分都能看懂。比较复杂而且重要的是AddEdgesObstacles 和 AddEdgesViaPoints。 via_point规定了轨迹应当经过这些点，否则会产生相应的cost。via_point边会与原规划的路径中与其距离最近的Pose顶点相连。

对于加速度约束，还要注意 vel_start_.first 和 vel_goal_.first，前者一般会添加，后者基本是false，信息矩阵一直是同一个。




1
2
3
4
5
6
7
8
9
10
11
void TebOptimalPlanner::clearGraph()
{
  // clear optimizer states
  if (optimizer_)
  {
    // neccessary, because optimizer->clear deletes pointer-targets 
    // therefore it deletes TEB states
    optimizer_->vertices().clear();  
    optimizer_->clear();
  }
}

局部规划可以让路径显示graph，在rviz中配置

参考：
TEB中的g2o问题的设置