沉默杀手
(七) Teb Optimal的路径规划
|路径规划TEB算法|
Word count: 1k|Reading time: 4 min
1
2
3
4
5
6
7
8
9
10
11
12
13
// 禁止配置参数的更改 during the following optimization step
boost::mutex::scoped_lock  cfg_lock(cfg_.configMutex() );
bool success = planner_->plan(transformed_plan, &robot_vel_, cfg_.goal_tolerance.free_goal_vel);
if (!success)
{
    planner_->clearPlanner(); // force reinitialization for next time
    ROS_WARN("teb_local_planner was not able to obtain a local plan for the current setting.");
    
    ++no_infeasible_plans_; // increase number of infeasible solutions in a row
    time_last_infeasible_plan_ = ros::Time::now();
    last_cmd_ = cmd_vel;
    return false;
}

clearPlanner()

不会停止规划，而是强制下次重新初始化planner，要停止继续规划，只能return。 如果本次导航失败或路径不好，出现一大堆TebPose缠绕，在下一次导航时，它们可能还在，要消除就需要clearPlanner();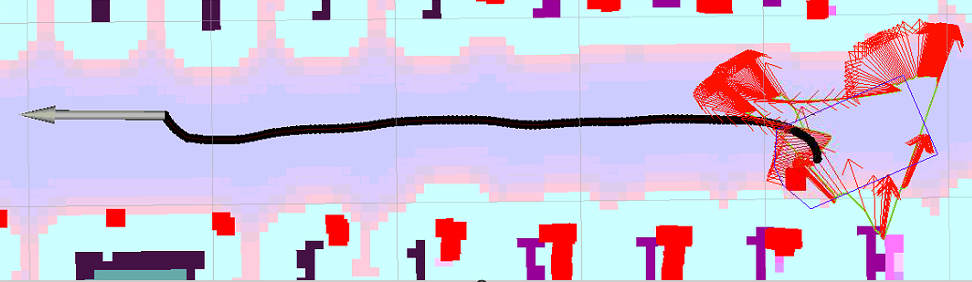
下次导航前，需要clearPlanner.png

下次导航前，需要clearPlanner.png


实际中用的是Homotopy Planner，但是它太复杂了，我们先看TebOptimal Planner，前者取的其实是 best Teb Optimal Planner 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
bool TebOptimalPlanner::plan(
            const std::vector<geometry_msgs::PoseStamped>&  initial_plan, 
            const geometry_msgs::Twist*  start_vel, 
            bool  free_goal_vel )
{
  ROS_ASSERT_MSG(initialized_, "Call initialize() first.");
  // 每次收到新目标时执行，然后pose size都是3
  if (!teb_.isInit() )
  {
      teb_.initTrajectoryToGoal(initial_plan, cfg_->robot.max_vel_x, 
      cfg_->robot.max_vel_theta,   cfg_->trajectory.global_plan_overwrite_orientation,
      cfg_->trajectory.min_samples,  cfg_->trajectory.allow_init_with_backwards_motion);
    // 0 个 intermediate samples, dt=1 --> autoResize  will add more samples 
    // before first optimization
  }
  else    // 热启动
  {
    PoseSE2 start_(initial_plan.front().pose);
    PoseSE2 goal_(initial_plan.back().pose);
    if (teb_.sizePoses()>0
        && ( goal_.position() - teb_.BackPose().position()).norm() < 
            cfg_->trajectory.force_reinit_new_goal_dist
        && fabs(g2o::normalize_theta(goal_.theta() - teb_.BackPose().theta())) < 
            cfg_->trajectory.force_reinit_new_goal_angular ) // actual warm start!

      teb_.updateAndPruneTEB(start_, goal_, cfg_->trajectory.min_samples);

      else // goal is too far away from BackPose, reinit相当于 isInit()为false
      {
          // 当导航较远的goal时，则首先clear轨迹序列，然后重新起点终点插值
          teb_.clearTimedElasticBand();
          teb_.initTrajectoryToGoal( start, goal, 0, cfg_->robot.max_vel_x, 
            cfg_->trajectory.min_samples, 
            cfg_->trajectory.allow_init_with_backwards_motion );
      }
  }
  // 当前从里程计获取的速度
  if (start_vel)
      // 赋值给 std::pair<bool, geometry_msgs::Twist> vel_start_; 
      setVelocityStart(*start_vel);   // start pose的速度
  if (free_goal_vel)            // 一般为 false
      setVelocityGoalFree();   // 这是唯一调用此函数的地方，不看了
  else
    // reactivate and 使用之前设置的速度 ( 如果未修改则是0 )
    vel_goal_.first = true; 

  return optimizeTEB(cfg_->optim.no_inner_iterations,  cfg_->optim.no_outer_iterations);
}

isInit()检查trajectory是否初始化: bool isInit() const {return !timediff_vec_.empty() && !pose_vec_.empty();}

1
2
3
4
5
6
7
8
9
10
11
12
13
// 清空 timediff_vec_ 和 pose_vec_， 之后 isInit返回 false
void TimedElasticBand::clearTimedElasticBand()
{
  for (PoseSequence::iterator pose_it = pose_vec_.begin(); 
             pose_it != pose_vec_.end(); ++pose_it)
      delete *pose_it;
    pose_vec_.clear();
  
  for (TimeDiffSequence::iterator dt_it = timediff_vec_.begin(); 
           dt_it != timediff_vec_.end();   ++dt_it )
      delete *dt_it;
    timediff_vec_.clear();
}

关于变量pose_vec_和timediff_vec_，看下篇文章


plan 函数涉及参数 max_vel_x, min_samples, force_reinit_new_goal_dist, allow_init_with_backwards_motion, free_goal_vel

TebOptimalPlanner::plan()主要是根据输入的初始路径初始化或更新时间弹性带(轨迹)的初始状态，设置了轨迹起始点以及速度加速度的约束， 最后调用 optimizeTEB() 函数：这里是核心中的核心，最关键的就是建图buildGraph和优化OptimizeGraph两个步骤

将轨迹优化问题构建成了一个g2o图优化问题,并通过g2o中关于大规模稀疏矩阵的优化算法解决，涉及到构建超图(hyper-graph)，简单来说 将机器人位姿和时间间隔描述为节点(vertex)，目标函数以及约束函数作为边(edge)。 graph中，每一个约束都为一条边，并且每条边允许连接的节点的数目是不受限制的。

建图是将路径的一系列约束加进去，比如与障碍物保持一定距离，速度、加速度限制、时间最小约束、最小转弯半径约束、旋转方向约束等，这些都转换成了代价函数放在g2o中，g2o优化时会使这些代价函数达到最小。

TebOptimalPlanner 的初始化

在TebLocalPlannerROS::initialize有这样一段

1
2
3
4
5
6
7
8
9
10
if (cfg_.hcp.enable_homotopy_class_planning)
{
   // 省略
}
else
{
  planner_ = PlannerInterfacePtr(new TebOptimalPlanner(cfg_, 
     &obstacles_,  robot_model,  visualization_,  &via_points_)  );
  ROS_INFO("Parallel planning in distinctive topologies disabled.");
}

TebOptimalPlanner的构造函数就一句initialize(cfg, obstacles, robot_model, visual, via_points);，实际是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void TebOptimalPlanner::initialize(const TebConfig& cfg, 
      ObstContainer* obstacles,
      RobotFootprintModelPtr  robot_model, 
      TebVisualizationPtr  visual, 
      const ViaPointContainer* via_points)
{    
  // init optimizer (set solver and block ordering settings)
  optimizer_ = initOptimizer();
  cfg_ = &cfg;
  obstacles_ = obstacles;
  robot_model_ = robot_model;
  via_points_ = via_points;
  cost_ = HUGE_VAL;
  prefer_rotdir_ = RotType::none;
  setVisualization(visual);
  // 在上面的 setVelocityStart 里赋值
  vel_start_.first = true;
  vel_start_.second.linear.x = 0;
  vel_start_.second.linear.y = 0;
  vel_start_.second.angular.z = 0;

  vel_goal_.first = true;
  vel_goal_.second.linear.x = 0;
  vel_goal_.second.linear.y = 0;
  vel_goal_.second.angular.z = 0;
  initialized_ = true;
}

initOptimizer()函数在(十) optimizeTEB 2 图优化的过程