沉默杀手HomeArchivesTagsCategories
(一) 理论和安装
|路径规划TEB算法|
Word count: 1.7k|Reading time: 5 min

理论

time elastic band(时间橡皮筋)从elastic band算法(1993年提出)优化而来。TEB的初始轨迹是全局路径传来的transformed_plan，中间插入N个控制橡皮筋形状的路径点（机器人位姿），在点与点之间定义时间差，转换为明确依赖于时间的轨迹，从而实现对机器人的实时控制。由于其模块化的形式，该方法可以扩展目标函数和约束。

TEB的创新在于考虑了动态约束和增加时间信息，如有限的机器人速度和加速度，将规划问题用加权多目标优化框架表示，也是一个bundle adjustment问题。在实时应用中，在线对全局路径进行大规模的计算往往是不可行的，TEB大多数目标函数是局部(local)的，因为它们依赖于一些邻近的中间 configurations。TEB的这种局部性会生成一个稀疏系统矩阵，才可以实现快速有效的大规模优化。作者写第一篇论文时(2012)，把约束表示为一个分段连续、可微的代价函数，到了下一篇论文(2013)，改成了使用g2o的图优化方法(利文伯格法)。

路径(Path)与轨迹(Trajectory)区别在于，轨迹包含了时间信息。所以TEB算法里老用Trajectory这个词。

各类目标函数

目标函数的梯度可以理解为作用在弹性带上的外力。

TEB的目标函数分为两类：

  • 约束：例如 速度、加速度限制
  • 目标：例如 最快、最短路径或者到障碍的距离

目标函数依赖的参数只取决于邻近位姿的子集。比如：

  • 速度(加速度)约束取决于两个(三个)连续的位姿和一个(两个)时间差。
  • 障碍物的清除和在中间路线上进行导航，只影响单个位姿和它的k个最近的邻居(实际上大约3-5)。
  • 遵守机器人的非完整运动学约束涉及到了两个相邻的位姿，这两个位姿位于一个常曲率的普通圆弧上

但是最快和最短路径是例外，显然是因为它们需要全局地依赖于所有的参数。

TEB同时考虑原始路径的via-point约束和避开障碍。这两个目标函数相似，不同之处在于via-point吸引路径，而障碍物排斥路径。

约束用到了几个顶点(待优化变量)，对应的就是几元边。 比如速度约束用到了两个位姿和一个时间差，是三元边。 加速度约束就是五元边。 障碍约束和via-point就是一元边。非完整运动学约束是二元边。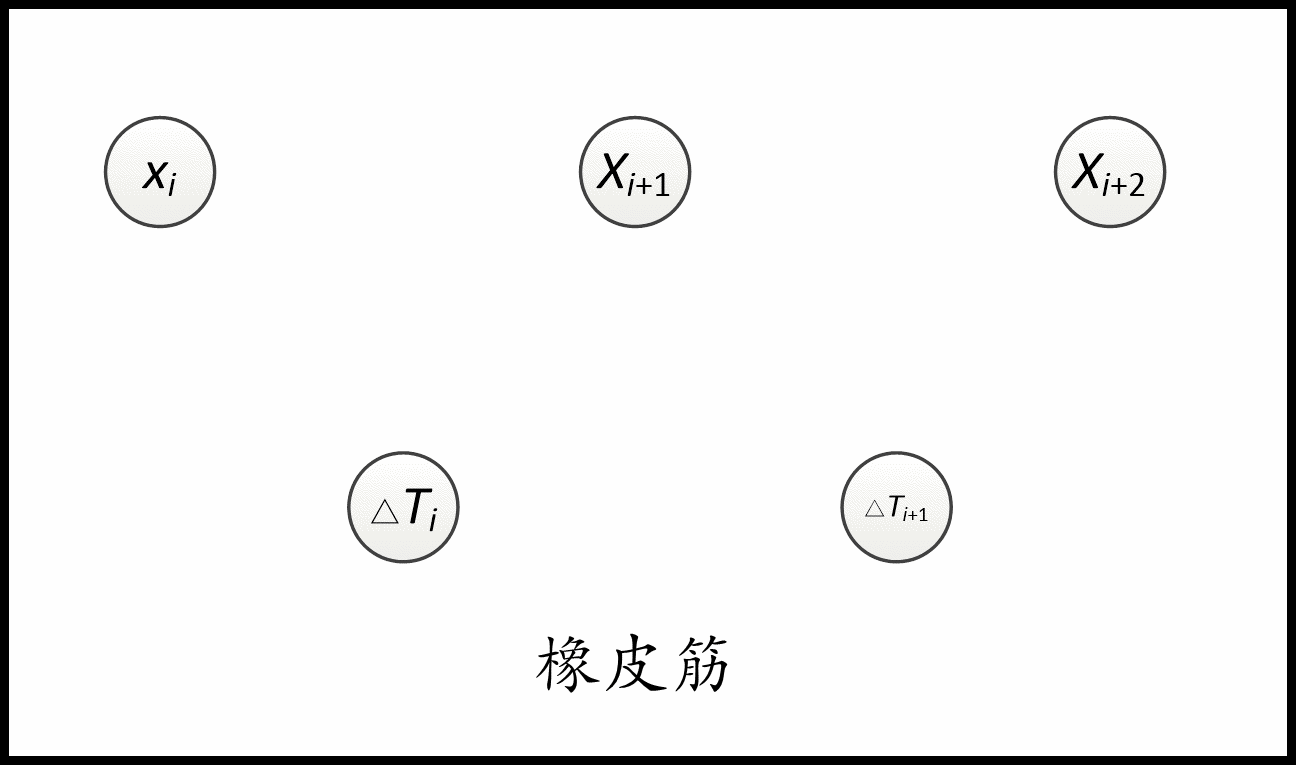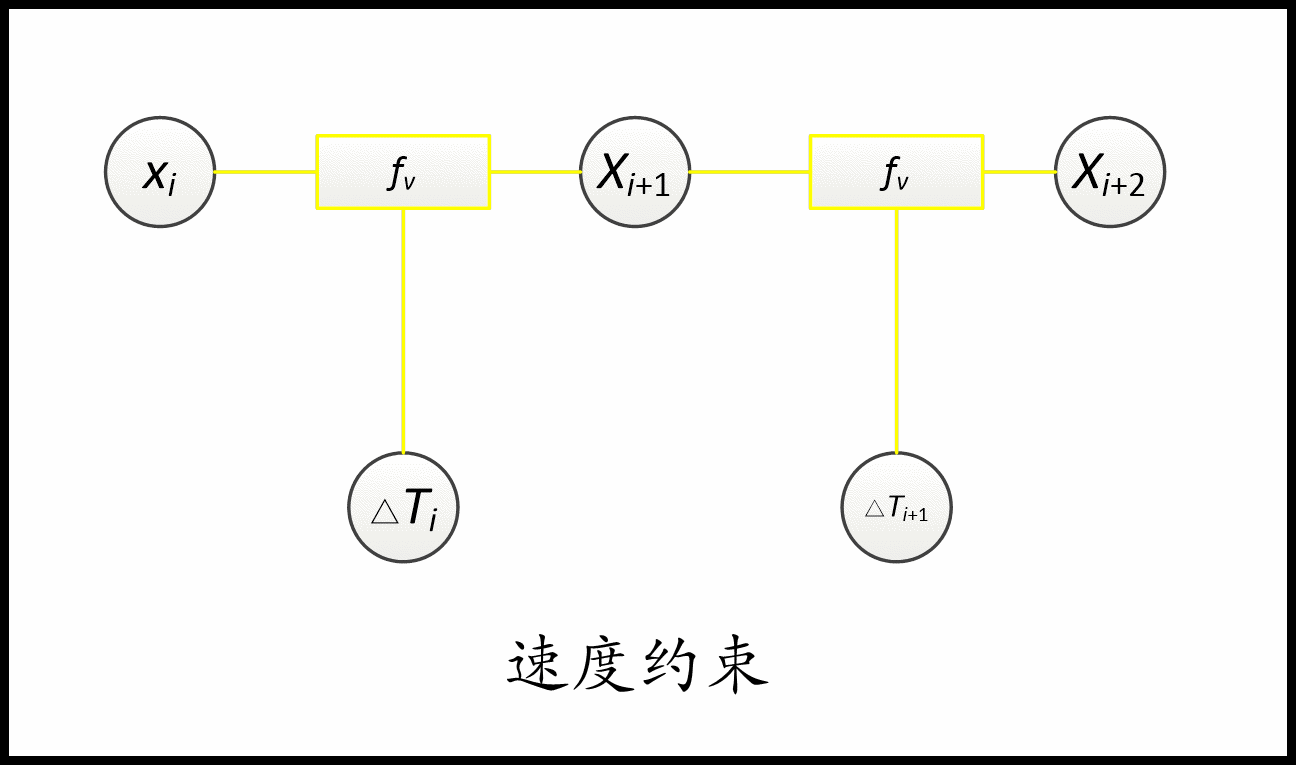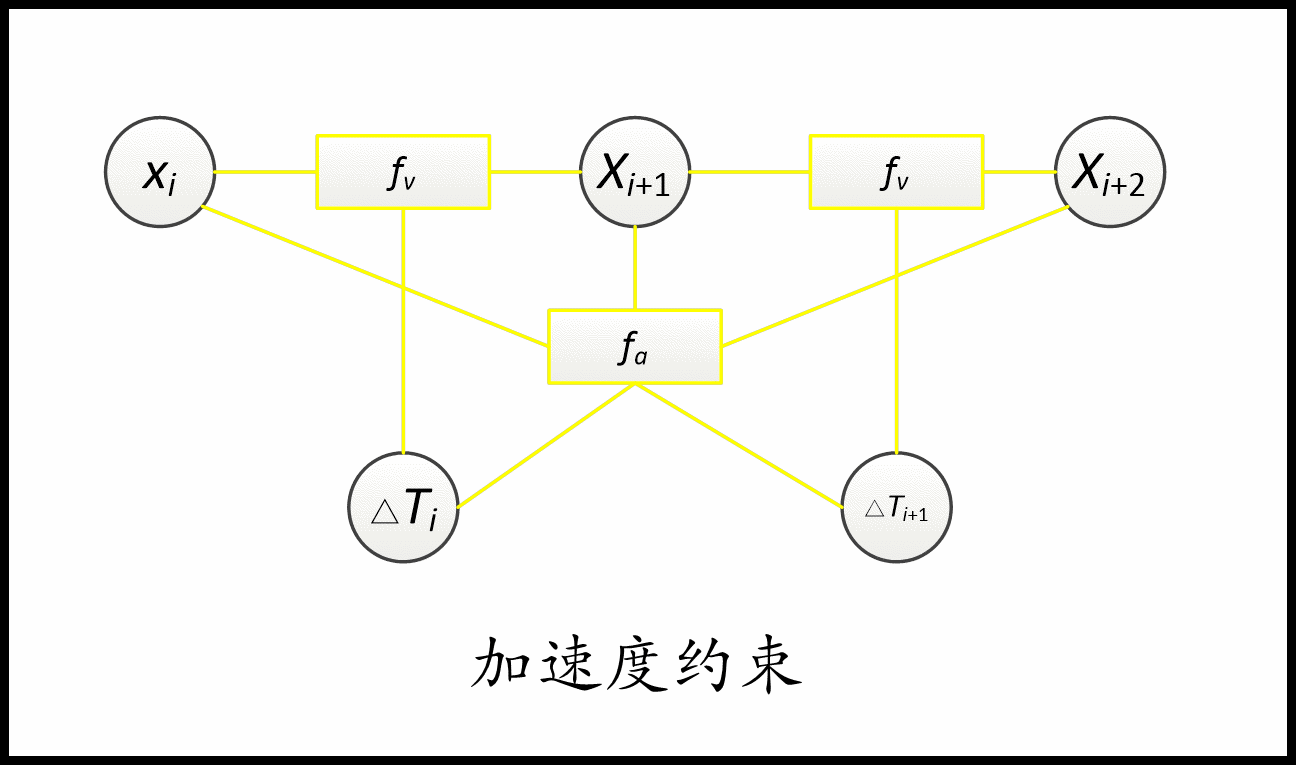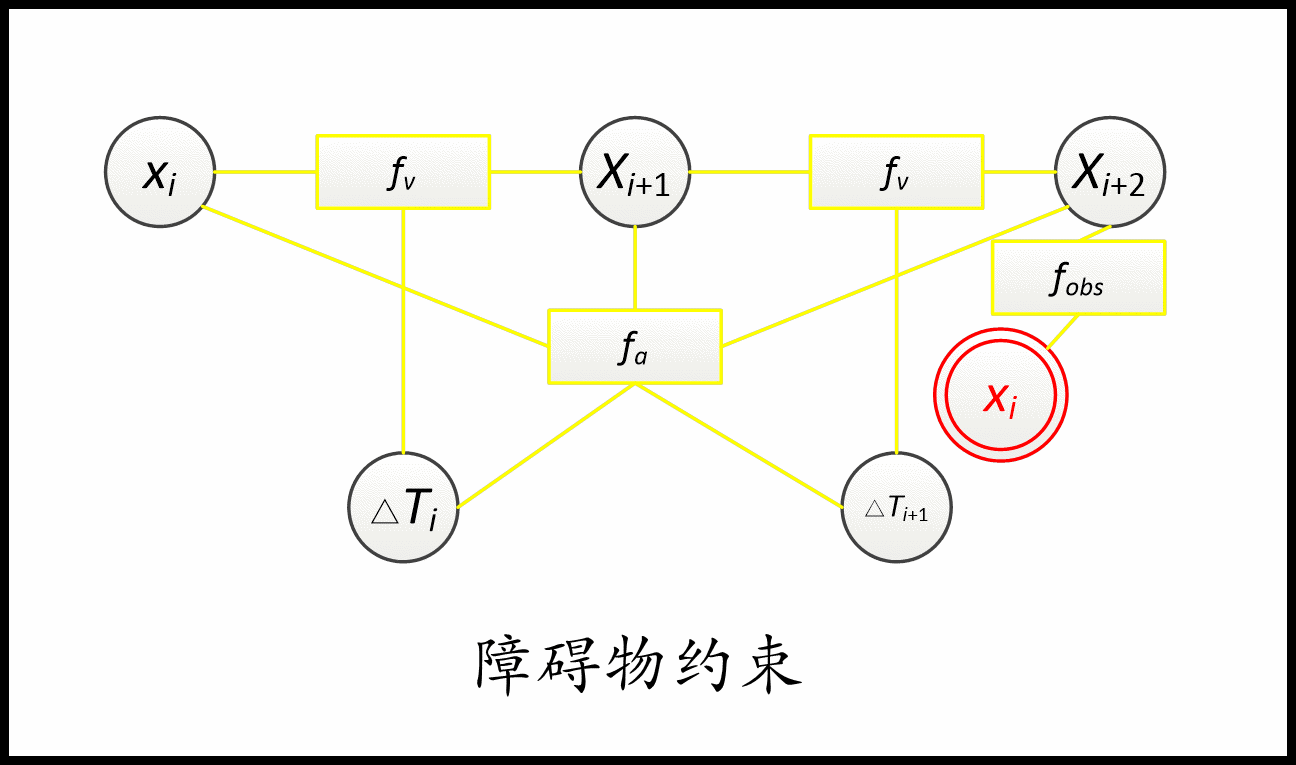
图的构建过程

为什么可以用非线性优化的框架？

平时所说的图优化的最小二乘形式是这样的：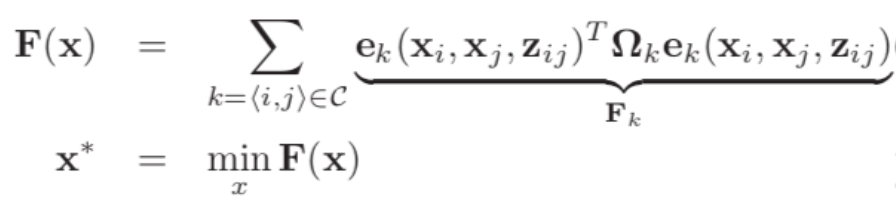
图优化的最小二乘形式

TEB所优化的目标函数是这样的：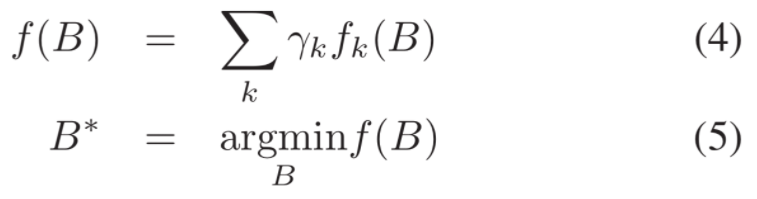
TEB的目标函数
我们先把上面的F(x)看成 ， 其中

图优化中，顶点是待估计的参数，观测数据构成了边。 TEB的待估计参数就是 ，也就是位姿和时间差的组合。 边表示目标函数 ，并连接多个顶点。

这个图的顶点vertexs是橡皮筋的状态（机器人姿态+时间），起点和终点当然是固定的，图的边是我们自己定义的优化目标函数。默认使用利文伯格法，优化器是g2o::CSparse

g2o框架在批处理模式下优化了TEB，因此每次迭代都会生成一个新的图。在一个机器人控制周期内对轨迹修改步骤进行多次迭代（四个循环包括5次利文伯格的迭代）。 g2o框架提供了两种基于Cholesky decomposition 的求解器: CHOLMOD 和 CSparse。默认是CSParse

对优化后的TEB进行验证，检查是否违反了硬约束，如果违反，在这种情况下机器人要么停止，要么重新调用运动规划器。

TEB每次迭代的平均运行时间依赖于TEB的维数，TEB的维数随位姿数(configurations)线性增长。对于10000多个states，对应大约2500种configurations。

Homotopy Planner

TEB中实现了两种规划器，一个就是普通的TebOptimalPlanner，另一个是HomotopyClassPlanner，HomotopyClassPlanner是一种同时优化多个轨迹的方法，由于目标函数的非凸性(非凸函数)会生成一系列最优的候选轨迹，最终在备选局部解的集合中寻求总体最佳候选轨迹，对应论文：《Integrated online trajectory planning and optimization in distinctive topologies》

optimizer本身只能找到局部最优轨迹，有时找到的路径invalid，所以一般都是用HomotopyClassPlanner。HomotopyClassPlanner类像是多个TebOptimalPlanner类实例的组合。HomotopyClassPlanner类中也会实例化一个由全局规划器生成的路径作为参考的对象。除此之外，它还会使用probabilistic roadmap (PRM) methods在障碍物周边采样一些keypoints，将这些keypoints连接起来，去除方向没有朝向目标点的连接和与障碍物重叠的连接。这样就形成了一个网络，然后将起始点和终点接入到这个网络。如下图所示：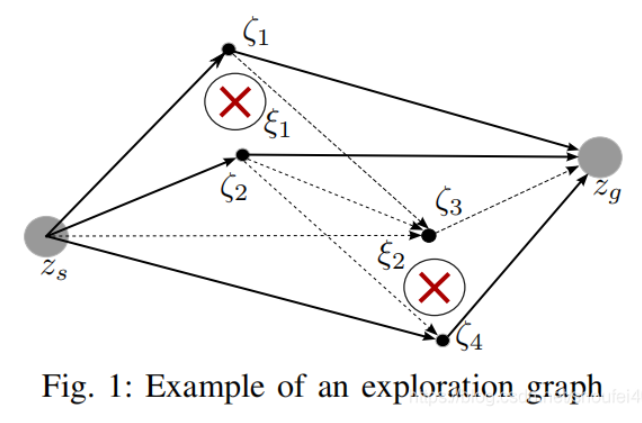

使用Depth First Search（深度优先方法）搜索所有可行的路径。将这些路径作为参考，实例化多个TebOptimalPlanner类的实例。采用多线程并行优化，得到多条优化后的路径。将这些路径进行可行性分析，选出代价值最小的最优路径。不得不说HomotopyClassPlanner类里的方法是一个鲁棒性和可靠性更高的方法。


安装

编译teb时报错，或者在没有编译TEB的计算机上通过.so运行TEB时会报错
加载TEB算法时报警.png
libteb_local_planner.so 缺链接库.png
实际的链接情况.png

因为没有安装g2o和ceres，不过不需要自己安装g2o。 先运行sudo apt-get install ros-melodic-teb-local-planner，这样会在/opt/ros里安装g2o，然后把g2o的so文件复制到/usr/local/lib

1
2
sudo cp /opt/ros/melodic/lib/libg2o* /usr/local/lib
sudo cp -r /opt/ros/melodic/include/g2o /usr/local/include

如果自己之前安装的g2o的相关共享库没有清除干净，解决方法为：

  • 删除/usr/local/include/g2o，指令为 sudo rm -rf /usr/local/include/g2o
  • 删除/usr/local/lib下有关libg2o*.so的库文件，先进入目录/usr/local/lib，然后挨个（可多个同时）删除: `sudo rm -rf libg2o.so libg2o_.so libg2o_*.so`

参考：
对ROS局部运动规划器Teb的理解
Trajectory modification considering dynamic constraints of autonomous robots
Efficient Trajectory Optimization using a Sparse Model—使用稀疏模型对有效轨迹进行优化