欧拉角
参考欧拉角的理解
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的,而刚体坐标系则固定于刚体,随着刚体的旋转而旋转。
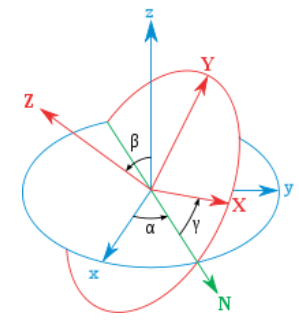
规定:XYZ坐标轴是旋转的刚体坐标轴;而xyz坐标轴是静止不动的实验室参考轴。
坐标系XYZ原与参考系xyz重合,旋转后,称xy平面与XY平面的交线为交点线,用英文字母N代表。zXZ顺规的欧拉角可以静态地定义如下:
α是x轴与交点线的夹角;
β是z轴与Z轴的夹角;
γ是交点线与X轴的夹角。
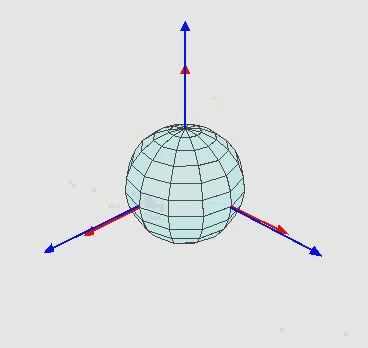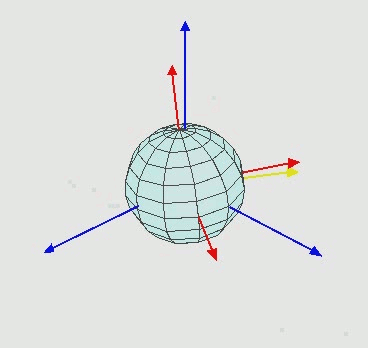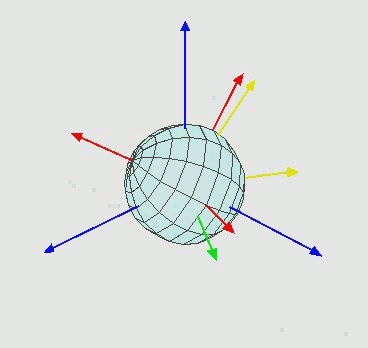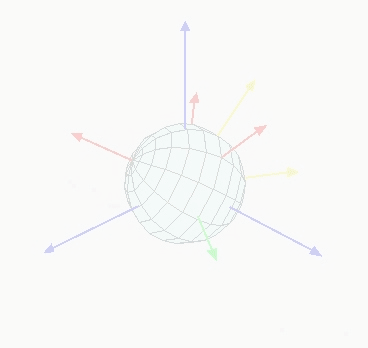
第一绕z轴旋转α,第二绕交点线(即X轴旋转后的轴)旋转β,第三绕Z轴旋转γ. 因此,此过程可分解为三个基本的旋转,从左到右依次代表绕着z轴的旋转、绕着交点线的旋转、绕着Z轴的旋转。即其旋转矩阵为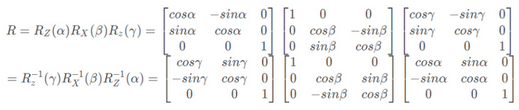
对于欧拉角,我们规定任何两个连续的旋转,必须是绕着不同的转动轴旋转。因此,一共有 12=3x2x2 种顺规。第一次旋转可以绕三个坐标轴中的任意一轴转动,有3种情况,第二次旋转可以绕除第一次旋转轴外的任意一轴转动,有2种情况,第三次旋转可以绕除第二次旋转轴外的任意一轴转动,有2种情况。
经典欧拉角:z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y
泰特-布莱恩角(Tait–Bryan angles):x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z
可以看出两者的区别是:经典欧拉角的第一个旋转角度和第三个旋转角度都是围绕同一个轴的,而Tait-Bryan角使用三个轴上的旋转角度去表示
- 内旋和外旋
同样的一个旋转,按旋转的坐标系又可分为内旋和外旋。
内旋是基于自身坐标系的旋转,旋转轴是动态的。内旋的旋转矩阵是按顺序右乘,
外旋是基于外部坐标系的旋转,旋转轴始终不变,也就是RPY。外旋的旋转矩阵是按顺序左乘。
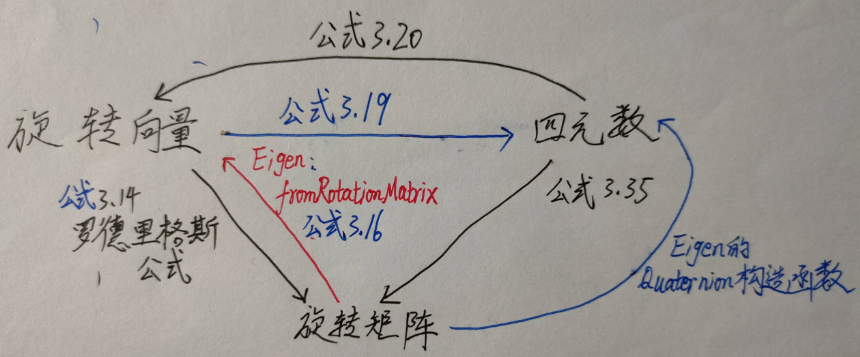
所以欧拉角要知道旋转顺序和是否定轴旋转,而旋转矩阵和四元数则是一个姿态就对应的一个旋转矩阵或四元数。除了万向锁问题,这也是SLAM不常用欧拉角的另一个原因。
在使用欧拉角的场合,大多数情况下都是采取外旋 XYZ
欧拉角和旋转矩阵
《SLAM十四讲》没有讲到这部分。坐标系A旋转到坐标系B,先绕Z轴旋转了yaw,这里遵循右手法则,大拇指朝坐标系方向,四指代表正向。或者说正向旋转是以沿X轴方向看,顺时针旋转为正向,否则为负向。那么相应的旋转矩阵为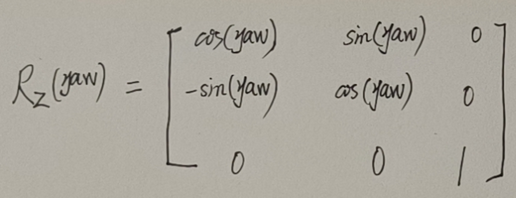
之后绕旋转后坐标系的Y轴旋转了pitch,之后绕旋转后坐标系X轴旋转了roll,最终的旋转矩阵如下,即依次左乘相应的矩阵
典型举例
如图,大坐标系是base_link,小的是 camera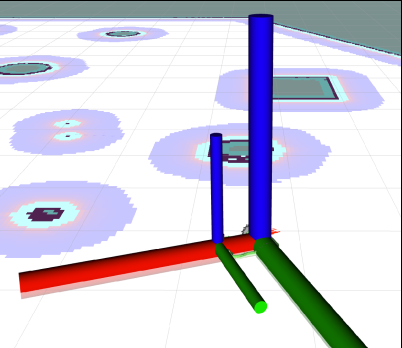
我们希望的坐标系关系是这样的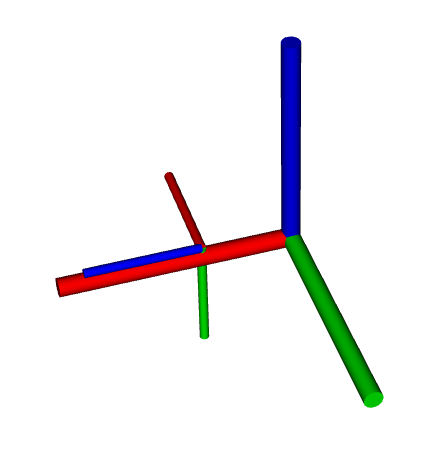
变化的过程是camera坐标系做内旋方式,也就是绕自身轴按照Z-Y-X的顺序旋转,即先绕自身轴Z,再绕自身轴Y,最后绕自身轴X,可得旋转矩阵(内旋是右乘)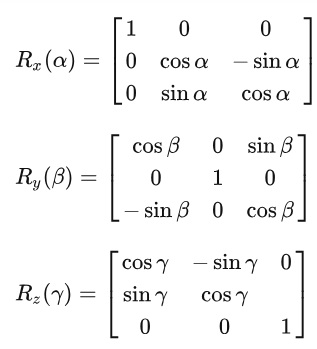
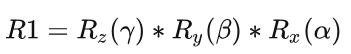
判断欧拉角的正负: 使用右手系,旋转轴正方向面对观察者时,逆时针方向的旋转是正、顺时针方向的旋转是负。这里先绕Z轴转 -90°,再绕X轴转-90°,camera就能变成希望的样子。
最终的旋转矩阵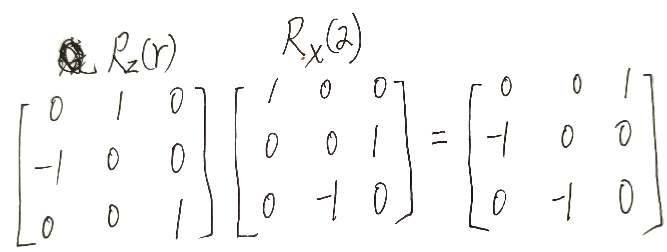
打开网站rotationconverter,在左上角的旋转矩阵输入计算的结果,在右下角出现XYZ对应的结果,而我们需要的是ZYX,即[ x: -90, y: 0, z: -90 ],这里并不是简单的把XYZ的结果倒序就行了。
我们要的欧拉角rpy就是 (-1.57, 0, -1.57)
旋转向量
旋转矩阵有几个缺点:SO(3)的旋转矩阵有9个量,但一次旋转只有3个自由度。因此,这种表达式冗余。而且对于旋转矩阵自身也有约束,它必须是正交矩阵,且行列式为1,这些约束会使求解变得困难。扩展到变换矩阵,就是用16个量表达了6个自由度的变换。
上面说的欧拉角是绕三个正交轴的依次旋转,其实任意旋转都可以用一个旋转轴和一个旋转角来表示。这只需要一个旋转向量即可,也就是说一个三维向量表示了旋转,再加上一个平移向量,这样就是6个自由度,没有冗余了。
四元数
Quaternion用一个冗余的变量解决了欧拉角的Singularity问题,在运算插值时也比较方便,因此四元数是程序中表示旋转最常用的一种表示方法
四元数——>旋转矩阵——>欧拉角 这个过程转出来的欧拉角,不可能是想要的。因为同一个四元数,可以用2个欧拉角来表示,而这个方法得到的结果有可能是用转角大于2π的方式表达的.
最好不要直接从四元数转欧拉角后,处理向量的旋转.
四元数加减法: 四元数的加法只需要将分量相加就可以了
四元数的共轭是让四元数的向量部分取负,记做 (w, -x, -y, -z)。 四元数和它的共轭代表相反的角位移,因为相当于旋转轴反向。
四元数的逆表示一个反向的旋转,定义为四元数的共轭除以它的模的平方,四元数和逆的乘积为实数 1。 如果是单位四元数,那么逆就是共轭
四元数的插值不能用简单的线性插值,而是用slerp。因为当时间t匀速变化时,代表姿态矢量的角速度变化并不均匀
Eigen::Quaterniond::Identity().slerp(t, q_last_curr)能够实现四元数的球面插值。t ∈ [0, 1]为插值点,q_last_curr为两帧之间的旋转四元数,即针对两帧之间的旋转而线性插入一个四元数。
cartographer中重新实现的slerp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29template <typename T>
std::array<T, 4> SlerpQuaternions(const T* const start,
const T* const end,
double factor)
{
// Angle 'theta' is the half-angle "between" quaternions. It can be computed
// as the arccosine of their dot product.
const T cos_theta = start[0] * end[0] + start[1] * end[1] +
start[2] * end[2] + start[3] * end[3];
// Avoid using ::abs which would cast to integer.
const T abs_cos_theta = ceres::abs(cos_theta);
// If numerical error brings 'cos_theta' outside [-1 + epsilon, 1 - epsilon]
// interval, then the quaternions are likely to be collinear.
T prev_scale(1. - factor);
T next_scale(factor);
if (abs_cos_theta < T(1. - 1e-5)) {
const T theta = acos(abs_cos_theta);
const T sin_theta = sin(theta);
prev_scale = sin((1. - factor) * theta) / sin_theta;
next_scale = sin(factor * theta) / sin_theta;
}
if (cos_theta < T(0.)) {
next_scale = -next_scale;
}
return {{prev_scale * start[0] + next_scale * end[0],
prev_scale * start[1] + next_scale * end[1],
prev_scale * start[2] + next_scale * end[2],
prev_scale * start[3] + next_scale * end[3]}};
}
