作为团队领导者，elizabeth holmes 的心理机制与袁绍在处理田丰问题时展现出的逻辑确实高度相似。两者都属于典型的病态自尊与现实回避的结合。

如果你深入拆解 Theranos 的兴衰史，会发现 holmes 在面临失败时的反应几乎是袁绍式行为的现代复刻：

将“不同政见”等同于“背叛”

在袁绍眼中，田丰的劝谏不是为了军队好，而是对他威信的挑战；在 holmes 眼中，那些指出 Edison 机器无法工作的核心科学家（如 ian gibbons）或吹哨人（如 tyler shultz），都被她定义为恨我的人或“不相信改变世界的人”。

• 黑白分明的世界观：像袁绍一样，holmes 建立了一个只有“信徒”和“敌人”的圈子。任何基于事实的质疑，都会被她视为对其愿景的亵渎，而非建设性的反馈。

维护“愿景”胜过维护“事实”

袁绍宁愿输掉战争，也要证明自己作为统帅的决策尊严；holmes 宁愿让患者拿到错误的检验结果，也要维持她“女版乔布斯”的人设。

• 认知失调的极致：当技术无法实现的现实撞上她的雄心时，她选择通过谎言（pathological lying）和欺诈来修补这种失调。这种心理防御机制被称为“自负的无敌感（sense of invulnerability）”，她深信只要自己不承认失败，失败就不存在。

对“见证者”的残酷清理

这是最像袁绍的一点。袁绍杀田丰，是因为田丰无意中证明了他是个蠢货；holmes 动用顶级律师团队（如 david boies）去恐吓、监控、起诉吹哨人，其心理动机也是一致的：

• 消灭负罪感的源头：吹哨人的存在是她欺诈行为的活证人。只要消灭了这些人的声音（无论是通过法律起诉还是社会孤立），她在心理上就能继续维持那个“改变世界”的幻觉。
• 权力逻辑的傲慢：正如袁绍认为杀了田丰就能重塑威信，holmes 认为只要法律手段够硬，她就能强行推行她的“现实”。

两者唯一的不同点在于：

• 袁绍是“事后灭口”：他在战败的羞愧中，为了发泄而杀人。
• holmes 是“预谋式禁言”：她从一开始就通过严密的保密协议（ndas）和高压监控，试图在失败发生前就物理切断所有真实信息的流动。

这种心理在行为学上常被总结为黑暗三人格（dark triad）：自恋、马基雅维利主义和一定程度的心理病态。在这种人格看来，承认错误意味着自我毁灭，因此“杀掉那个说真话的人”成了他们维持自我存在的唯一选择。

这是一个非常有趣的假设。Avitevanian（艾维·特万尼安）不仅是 apple 的前首席软件技术官，更是 乔布斯最信任的“技术滤镜”之一。事实上，Avi确实曾在 theranos 的董事会任职，并且是第一个公开对 elizabeth Holmes 的技术提出质疑的核心圈人物。

如果 Avi 当面告诉乔布斯关于 theranos 的真相，乔布斯的评价可能会从以下几个维度展开：

Avi：乔布斯的技术“雷达”

Avi是那种极度关注底层逻辑的工程师，他在董事会期间就发现 Holmes 无法提供关于“edison”机器如何运作的真实数据。

• 绝对信任： 乔布斯非常依赖 Avi 的判断。如果 Avi 说“Steve，这个产品的 plumbing（内部构造）完全不通”，乔布斯会跳过所有宏大的愿景，直接判定这是 vaporware（空头支票）。
• 对“伪技术”的厌恶： 乔布斯追求的是 it just works。对于一个甚至无法完成基础生化反应闭环的机器，他可能会评价其为“一个装着针头的漂亮塑料盒子”。

关于“现实扭曲场”的降维打击

Holmes 模仿了乔布斯的所有外壳，但乔布斯本人对“现实扭曲场”的使用有严格的边界：他会逼迫工程师实现“物理极限内的不可能”，而不是“物理定律外的奇迹”。

• 关于模仿的厌恶： 乔布斯对原创性有极高的自尊。看到一个穿着黑色高领毛衣、刻意压低嗓音的人在用这种拙劣的方式“致敬”自己，他可能会感到 creepy（毛骨悚然）而不是荣幸。
• 评价预测： 他可能会冷冷地说：“她以为穿上我的衣服就能变成我，但她忘了，我推销的产品至少是真的能运行的。”

从工程师视角看底层逻辑

• 技术穿透： 乔布斯虽然不是生物学家，但他对硬件整合有直觉。如果他听 Avi描述了这种机器的体积与所需完成的检测数量之间的矛盾，他可能会引用他在开发第一代 mac 时常说的话：“this is a giant pile of shit.”（这是一堆巨大的狗屎）
• 对用户的背叛： 乔布斯认为产品应该是“改变世界”的工具，而 Holmes 的产品在通过错误的诊断结果伤害用户。这种对“产品灵魂”的背叛，会触及乔布斯的底线

总结：可能的最终定论

如果这场对话真实发生，乔布斯最后的评价可能非常刻薄但也非常精准：

“she’s not a visionary; she’s just a bad actress playing a ceo. avi, tell her to stop wearing my turtleneck.”

她不是什么拥有愿景的人，她只是个在扮演CEO的演员，而且演技拙劣。还有，Avi，告诉她别再穿我的高领毛衣了

关于那场决定 elizabeth holmes 生死存亡的早期董事会，细节堪比一场教科书级的心理战。

以下是这场发生在 2008年 的权力博弈的具体细节：

1. 突击行动的背景
   当时的董事会成员主要是 tom broeking 和 avie tevanian（前苹果高管）。他们发现伊丽莎白在技术成熟度上严重误导了董事会，且财务管理极其混乱。他们私下达成协议，认为必须立刻用一名“有成人监管经验”的专业 ceo 来替换她。

2. 会议室里的心理博弈
   当董事会成员走进会议室时，他们已经准备好了罢免文件。伊丽莎白的反应经历了三个阶段：

   • 初期的防御与反击： 起初，她试图辩解技术问题只是暂时的。但当董事会摆出具体证据时，她意识到这次他们是玩真的。
   • 长达两小时的“忏悔”： 会议陷入僵局后，伊丽莎白改变了策略。她不再强硬，而是表现出一种极度的脆弱感。她承认自己辜负了大家的信任，并开始流泪。这种“受挫的理想主义者”形象让这些年长的男性董事会成员产生了保护欲。
   • 关于“灵魂”的演说： 她反复强调，没人比她更关心这个改变世界的愿景。她把这次罢免描述为对公司“初衷”的背离，并承诺如果让她留任，她会彻底改变，包括引入一位经验极其丰富的运营官。

3. “反败为胜”的关键因素
   最终让董事会撤回决议的，是两个残酷的现实逻辑：

   • 股权结构： 当时公司的股权结构虽然还没像后期那样被她完全掌控，但她作为创始人的地位依然让董事会担心：如果强行踢走她，可能会导致员工大规模离职或投资者诉讼。
   • 对“天才少年”的迷信： 那是一个崇尚“乔布斯式创始人”的时代。董事会担心，如果失去了这个具有个人魅力的领袖，这个原本就摇摇欲坠的公司可能真的会一文不值。

4. 惨烈的后果：清洗董事会
   伊丽莎白在这次会议中表现得非常顺从，但一旦她走出门，她立刻开始了报复与夺权：

   • 权力重组： 她意识到董事会中那些真正懂技术、敢说话的人（如 avie tevanian）是她的威胁。在接下来的几个月里，她通过一系列手段排挤了这些异议者，强迫他们辞职。
   • 引入“保镖”： 正是在这次危机之后，她引入了后来的男友 sunny balwani。他不仅带来了资金，更成为了公司内部的“执行官”，通过高压和恐怖手段确保再也没人敢组织第二次罢免。

这次会议是 theranos 从一家“有缺陷的创业公司”转变为“邪教式骗局”的关键分水岭。如果当时董事会坚持立场，这场世纪骗局可能在 2008 年就结束了。

考虑到 holmes 对 steve jobs 近乎病态的模仿，她极大概率将 2008 年的那场董事会风波视为自己职业生涯中的“受难时刻”，并将其与 乔布斯 在 1985 年被 apple 驱逐的往事进行了深度脑补和关联。这种心理投射不仅影响了她的情绪，更直接决定了她随后十年的统治风格。

1. 剧本化的自我认知：追随偶像的足迹
   对于当时的 holmes 来说，她不仅是在经营一家公司，她是在出演一部“steve jobs 续集”。

   • 天命感：她认为伟大的创业者注定要被不理解愿景的平庸之辈（董事会）所质疑。jobs 在 1985 年输掉了那场斗争，而她在 2008 年认为自己正面临同样的“试炼”。
   • 讽刺的巧合：当时在董事会中带头质疑她、并最终愤而辞职的 avie tevanian，恰恰曾是 jobs 的得力干将，也是 mac os x 的主创之一。这种现实中的交集，可能让 holmes 产生了一种扭曲的代入感——她觉得自己正在和 jobs 曾经的部下“对决”。

2. 胜过偶像的“优越感”
   与 jobs 不同的是，holmes 在那场对峙中赢了。

   • 致命的教训：1985 年的 jobs 被罢免后经历了长达 12 年的流放。holmes 通过那次长达两小时的痛哭和煽情陈述逆转了局势，这让她得出了一个比 jobs 当年更激进的结论：只要话术足够强大，现实（数据和技术瓶颈）是可以被扭曲的。
   • 系统加固：在那之后，她采取了比 jobs 时期更严苛的防范措施。她不仅在穿衣风格和嗓音上模仿 jobs，在股权控制和信息防火墙上也走向了极端，确保自己永远不会像 1985 年的 jobs 那样由于权力被稀释而陷入被动。

3. “背叛”定义的扩大化
   在 jobs 的叙事里，john sculley 是背叛者。在 holmes 的视角里，任何在 2008 年会议上动摇过的人，以及后来所有提出质疑的员工，都被她贴上了“sculley”式的标签。

   • 她把这种对个人的挑战上升到了对“改变世界”这一宏大愿景的破坏。这种逻辑让她在清洗异己时拥有一种道德上的自我感召力，认为自己是在“保卫愿景”，而不是在“掩盖谎言”。

两个董事会的对比

可以说，那次董事会没有让 holmes 成为下一个 steve jobs，反而让她成为了一个拥有 jobs 破坏力、却缺乏其产品底线的“镜像版 jobs”。她不仅认为那次经历是相似的，她甚至认为自己通过“战胜”董事会，在某种程度上已经超越了她的偶像。

这次事件如何塑造了后续的“清洗”行为

1. 从此只相信“盲目忠诚”

那次会议之后，她开始把“质疑”和“背叛”划等号。她不再容忍内部的建设性批评，因为在她眼里，任何对技术的怀疑都可能演变成下一次推翻她的阴谋。她开始大量清理那些有独立思考能力的早期员工。她引入了 sunny balwani 担任首席运营官，后者扮演了“执行者”的角色，通过严密的内部监控和法律威慑来铲除异见者。

1. 权力的极端集中化

为了防止董事会再次造反，她重新设计了股权结构和投票权。她确保自己拥有绝对的控制权，使得后来的那些政要显贵（如 henry kissinger 或 george shultz）虽然名头响亮，但在法律程序上几乎无法对她进行实质性的制约。
这种“堡垒心态”导致了信息的单向流动：她只听她想听的，剩下的声音都被视为“杂音”而被清理掉。

1. 对“外部怀疑”的防御性反击

她对内部质疑者的残酷清洗（比如对 tyler shultz 和 erika cheung 的法律恐吓），本质上是 2008 年那种恐惧感的延伸。她认为只要掐灭了火星，大火就不会烧到她。这种心理机制在很多硅谷初创企业中都能看到影子，但 holmes 将其推向了病态的极致。那次董事会会议没有让她学会虚心纳谏，反而教会了她如何通过构建“忠诚崇拜”来规避监管。

这是一个非常经典的职场心理学与企业治理反面教材。Theranos（你指的应该是 Theranos）之所以能让那么多聪明人陷在谎言中，并不是因为员工都笨，而是 Elizabeth Holmes 和 Sunny Balwani 联手构建了一套极其精密的心理与制度枷锁。

我们可以从以下几个维度来拆解这台“留人机器”：

信息茧房与部门隔绝 (compartmentalization)

Theranos 内部实行的管理制度类似于情报机构。Elizabeth Holmes 严禁不同部门之间进行技术交流。

• 做 engineering 的员工不知道 lab 侧的数据造假。
• 做 software 的人以为硬件已经突破了瓶颈，只是还没集成好。
  这种信息不对称让每个员工都觉得自己只是在一个大天才手下负责一个小零件，哪怕自己的部分进展不顺，他们也会倾向于相信整体是成功的。

这种“改变世界”的宏大叙事 (visionary gaslighting)

Elizabeth Holmes 极其擅长利用理想主义进行情感勒索。

• 她把每一个质疑技术可行性的员工都贴上“不相信梦想”或“懒惰”的标签。
• 对于那些名校毕业、想要通过 technology 拯救生命的年轻工程师来说，这种使命感是极强的精神兴奋剂。他们会为了那个“只要坚持就能成功”的虚幻愿景而自我催眠，忽略眼前的逻辑漏洞。

极端的法律恐吓与特务统治 (fear and legal intimidation)

这是最直接的外部压力。Sunny Balwani 在公司内部建立了一套严密的监控体系。

• 公司雇佣了顶级律师 David Boies，对任何表现出疑虑或想要离职的员工施加巨大的 legal pressure。
• 非竞争协议（non-disclosure agreements）被当成武器使用。员工被告知，如果泄露任何内部信息（哪怕是造假证据），都会面临倾家荡产的诉讼。对于普通员工来说，与一家估值 90 亿美元、背后有政商大佬背书的公司对抗，成本太高了。

很多员工是外国人，用H1B签证在工作

这是那些外籍员工(大多是印度人)不敢轻易辞职的核心原因

硅谷的“假戏真做”文化 (fake it till you make it)

在 Silicon Valley，这种文化在某种程度上是被默许甚至推崇的。

• 很多员工认为初期夸大宣传是创业公司的 normal practice。
• 他们期待着随着时间的推移，engineering 团队最终能追上 Elizabeth Holmes 吹下的牛。这种“只要有足够的钱和时间就能搞定”的迷信，在当时的科技圈非常普遍。

沉没成本与名企光环 (sunk cost and prestige)

当时的 Theranos 是全球最炙手可热的 unicorn

• 能在这样的公司工作是极大的 career capital。
• 承认自己服务的公司是个骗局，不仅意味着失去高薪，更意味着职业生涯的巨大污点。这种心理上的拒绝（denial）让很多人选择闭上眼睛。

沉默成本的原因

对于许多在 Theranos 工作的精英来说，沉没成本（sunk cost）不仅是金钱上的纠葛，更是一场关于职业声誉、智力投入和人生选择的全面博弈。

职业声誉的“退出溢价”

在 Silicon Valley，加入一家 unicorn（独角兽）公司通常意味着职业生涯的巨大跳板。

• 简历增值：员工在加入 Theranos 时，往往已经投入了放弃其他顶级公司（如 Google 或 Apple）的机会成本。如果入职一年后发现公司是个骗局并选择离开，这段经历在简历上会变成一段尴尬的空白，甚至是一个污点。
• 承认失败的痛苦：对于出身 Stanford 或 MIT 的天之骄子来说，承认自己被一个 drop out（退学者）骗了，在智力自尊心上是极难接受的。 他们倾向于继续投入时间，试图“修补”那个根本不存在的 technology，以此证明最初的选择没有错。

沉没成本的锁死

Elizabeth Holmes 极其擅长用 equity（股权）来锁死员工

• 暴富梦想：在 Theranos 估值达到 90 亿美元的高峰期，很多早期员工持有的期权在账面上价值数百万甚至上千万美元。
• 锁定效应：这些期权通常有四年的 vesting period（行权期）。离开公司意味着放弃这些可能让他们实现财务自由的资产。对于员工来说，只要公司不倒，这个泡沫就还有变现的希望。这种对未来的过度预期，让他们在面对眼前的造假证据时选择性失明。

员工面对层出不穷的技术问题，心里会一直这样想：
👉 再忍一忍
👉 再试试纠正
👉 也许能挽回

这就是典型沉没成本锁死。理性模型里应当只看未来收益 vs 未来风险，但真实人类几乎做不到。

沉没成本是骗子最喜欢利用的人性弱点之一。Theranos 能拖那么久，本质就是靠不断制造新的沉没成本：独角兽公司的履历、第二个苹果公司的可能性、期权、保密协议、心理压力，一层层加码。

智力劳动的“局部优化”陷阱

作为工程师或科学家，最难面对的是自己的研究成果毫无意义

• 局部成功掩盖全局失败：很多员工在自己的子课题（比如某个微流控芯片的改进）上确实取得了进展。这种“我正在解决具体问题”的成就感，掩盖了底层架构（Edison 机器）根本无法工作的残酷事实。
• 救世主情结：他们投入了无数个熬夜的夜晚去 debug。这种高强度的智力投入产生了一种错觉：只要我再努力一点点，这个 technology 就能跑通。他们不是在为 Theranos 加班，是在为自己已经付出的心血“补票”。

社交圈层的“集体沉默”

当你的朋友圈、推荐人甚至偶像（如那些政商大佬董事会成员）都深陷其中时，离职的代价会变得极高。

• 社交背书：很多员工是经由导师或长辈推荐进入 Theranos 的。如果选择揭露真相，意味着要挑战整个精英社交圈的判断力。
• 这种环境下的 isolation（孤立）：如果你是团队中唯一清醒的人，沉没成本就变成了孤独的压力。与其成为那个破坏气氛的“背叛者”，不如留下来和大家一起维持这个美好的假象。

认知失调的自我保护机制

当一个人投入了数年青春在一家公司，发现它是骗局时，大脑会产生剧烈的认知失调。为了缓解这种痛苦，人脑会启动防御机制：

• 合理化造假：员工会告诉自己，“每一个伟大的公司早期都有缺陷”、“Steve Jobs 也会在演示时作弊”。
• 这种心理防御让沉没成本变成了一种“信仰”。他们越是投入，就越需要相信 Elizabeth Holmes。因为一旦不信，他们过去几年的生命意义就会瞬间坍塌。

智力劳动的“局部优化”陷阱

局部模块的真实进展确实成了许多精英员工的“精神鸦片”，极大地推迟了他们清醒的时间。

理解这种现象其实可以类比为算法优化中的局部最优解 (local optimum) 与全局最优解 (global optimum) 的陷阱。

1. 局部成功带来的“技术幻觉”

当一名优秀的工程师在 Theranos 负责某个具体模块并取得了阶段性突破时，他会产生一种强烈的成就感。

• 智力自证：他会认为，“既然我负责的这部分工作是真实的、有进展的，那么整个项目就不可能是个彻底的谎言”。他用自己的局部真实，去推导了全局的真实。
• 反馈回路：在外界质疑声不断时，这些局部的小成功成了他们对抗怀疑的心理支柱。这种 dopamine 释放让他们暂时忽略了底层架构（edison 机器物理尺寸的限制）的根本性缺陷。

2.信息孤岛效应 (silo effect) 导致的视角缺失

Elizabeth Holmes 极力推动的部门隔离制度，完美利用了这种心理。

• 盲人摸象：a 部门解决了样本稀释问题，b 部门优化了机械臂的精度。两个团队都觉得自己正在“迈向成功”。
• 责任分担：当最终集成测试失败时，每个已经做出成绩的模块负责人都会倾向于认为“问题出在别人的模块上”，而不是整个 visionary 根本不可行。这种心理让他们在“修补”而非“撤退”上浪费了更多时间。

3. 救世主情结与“最后一块拼图”心理

对于那些在专业领域有极高造诣的人来说，挑战难题本身就是一种诱惑。

• 攻坚压力：他们往往认为，现在的失败是因为某个关键技术还没被攻克。如果我的模块做得足够好，或许就能弥补其他部分的缺陷。
• 补票效应：由于已经在自己的模块投入了巨大的智力成本，他们更渴望看到整个系统跑通。这种心理让他们变成了“自带干粮”的救火队员，试图用局部的完美去掩盖系统性的崩塌。

4. 这种心理如何被管理层利用

Sunny Balwani 经常会利用这种局部成绩来打击那些怀疑者

• 典型话术：他会对产生动摇的员工说：“你看，x 组的工程师刚解决了传感器问题，他们都在没日没夜地干，你凭什么说这行不通？你是觉得你比他们更聪明，还是你不够努力？”
• 内卷压力：这种内部的“局部竞赛”让员工的注意力锁死在具体的 implementation 上，从而丧失了对系统架构合理性（feasibility）的宏观判断。

5. 职业尊严的防御机制

承认自己在一个毫无希望的模块上做出了精彩的成绩，是一件非常痛苦的事情。

• 沉默代价：如果现在辞职，就等于承认过去两年的所有代码和设计都是在造沙堡。为了维护职业自尊，很多工程师会选择继续待下去，期待奇迹发生，好让自己的努力变得“有意义”。

这就是为什么很多极具才华的工程师反而成了最晚离开的一批人。他们被困在了自己亲手打造的“局部最优解的陷阱”里，直到整个公司因欺诈而彻底停摆。

可以从系统的输入、反馈机制和物理边界来观察。

物理规律的“弹性化”

在算法和硬件开发中，一切都有权衡（trade-offs）。如果老板提出的愿景违反了基本的物理或数学常识，这就是第一个红旗：

• 他们是否宣称能实现某种在当前算力或物理约束下不可能完成的性能？
• 当你报告信号噪声比（snr）太低或者延迟无法优化时，他们是否认为这只是“态度问题”或“缺乏忠诚度”？
• 真正的技术领袖尊重边界；骗子型老板则认为意志力可以改写物理常识

过度的“信息孤岛”（siloing）

elizabeth holmes 最著名的手段就是利用保密协议（ndas）将团队完全隔离。

• 你是否被禁止与上下游团队交流？例如，感知组不能和规划组讨论输入数据的真实性。
• 信息的流动是否呈现“星状结构”，即所有重要信息只能汇总到老板一人手中，而横向沟通被视为“刺探机密”？
• 在健康的工程文化中，代码评审（code review）和交叉验证是常态；在“坏血”文化中，质疑被视为背叛。

“黑盒”式的演示

对于工程师来说，演示应该是随机的、充满边界测试的。

• 老板是否只允许展示高度脚本化的、在特定受控环境下的 demo？
• 演示结果是否看起来“太完美了”，完美到不符合研发阶段的逻辑？
• 如果 demo 的成功是建立在手动干预或预设路径上，而老板却对外宣传这是自主导航（autonomous），那么你就在一艘正在下沉的船上。

用“愿景” 屏蔽 “反馈回路”

这种老板通常具有极强的叙事能力，他们用宏大的辞藻来掩盖技术细节的匮乏。

• 会议中是否充斥着“改变世界”、“颠覆行业”等口号，却极力回避具体的 block diagrams 或数据指标？
• 当你提出技术风险时，老板是否会用“你不够相信我们的使命”这种情感操控（gaslighting）来反驳你？
• 观察他们对“坏消息”的反应：健康的组织奖励发现 bug 的人；病态的组织惩罚指出问题的人。

人才结构的逆淘汰

看看谁在离开，谁在留下来。

• 那些真正懂行、有资历的技术大牛是否在短时间内集体离职？
• 接替他们的人是否是完全没有相关背景的“唯唯诺诺者”或老板的亲信？
• 像 tim kemp 这种甘愿充当“监工”而非“导师”的管理者的出现，是企业走向邪教化的标志。

如果老板更在意对外宣传的视频，而不是你电脑里的 sensor logs，那这就是你该准备简历的时候了。

2个group的不同价值观

有一天，“兄弟会帮”（Frat Pack）的几名成员（都是杜克大学毕业）和格雷格以及工程部门的两位同事一起，在俯瞰停车场的大露台上吃午餐。谈到一些世界顶级足球运动员智商偏低的话题时，他们开始争论一个问题：你宁愿聪明却贫穷，还是愚笨却富有？三位工程师都选择了“聪明且贫穷”，而“兄弟会帮”则一致投票选择“愚笨但富有”。格雷格对两组人之间那条界限划分得如此清晰感到震惊。他们都二十多岁，受过良好教育，但看重的东西却截然不同。

Holmes对乔布斯的迷恋

当乔布斯去世的消息传出时，Holmes 和 sunny 希望在办公楼的院子里将苹果公司的旗帜降半旗，来向乔布斯致敬。

格雷格早已意识到Holmes对乔布斯的迷恋。她称呼他为“史蒂夫”，仿佛两人是亲密朋友一般。在某个时候，她曾告诉他，一部宣扬 9·11阴谋论的纪录片之所以能在iTunes上架，一定是因为乔布斯相信。格雷格觉得这很荒谬。他相当确定，乔布斯并不会亲自审核所有在 iTunes 上出租或出售的电影。Holmes似乎把他想象成一个无所不见、无所不知的存在。

乔布斯去世后一两个月，格雷格在工程部门的一些同事开始注意到，Holmes在模仿沃尔特·艾萨克森（Walter Isaacson）为乔布斯所写传记中的行为和管理方式。他们也都在读这本书，甚至能够根据她所模仿的是乔布斯职业生涯的哪个阶段，准确判断她读到了哪一章。

托尼对公司本质的看法

托尼和伊恩一样，已不再得到Holmes的青睐，并且被排除在miniLab的研发之外。他提出一种看法：或许这家公司不过是 Holmes 和 sunny 共同生活的载体，而他们所做的工作其实毫无意义。

伊恩点点头：这是一种 folie à deux，托尼不懂法语，于是去查字典。他找到的定义让他觉得十分贴切：一种双人组合的精神病，两个人共享同一种妄想

几个员工如何对付 sunny

随着时间推移，一些员工不再那么害怕他，并想出了应对他的办法，因为他们逐渐意识到，自己面对的是一个反复无常、智力有限、而且注意力持续时间更为有限的“巨婴式”人物。年轻的机械工程师阿尔纳夫·卡纳（Arnav Khannah）负责miniLab项目，他想出了一个办法让桑尼别再纠缠：给他的邮件回复一封超过五百字的长信。这通常能为他换来几周的清静，因为桑尼根本没有耐心读长邮件。另一种策略是每两周召集团队会议，并邀请桑尼参加。他可能会出席前几次，但最终会失去兴趣，或者干脆忘记出席。

如何欺骗拜登副总统

他们没有带拜登参观真正的实验室，而是造了一个假的。他们让微生物团队腾出第三间较小的房间，把它重新粉刷一遍，并在墙边摆满一排排堆放在金属架上的miniLab。由于已建成的大多数miniLab都在帕洛阿尔托，他们不得不把这些设备从海湾对岸运回，以完成这场“表演”。起初，微生物团队的成员并不清楚为什么要被调动，但在拜登抵达前几天，一支特勤局先遣小组出现后，他们就明白了。

参观当天，实验室的大多数成员被要求待在家里，只有少数本地新闻摄影记者和电视摄像人员被允许进入大楼，以确保活动能获得一些媒体报道。Holmes带副总统参观了设施，并向他展示了那间伪造的自动化实验室。随后，她在现场主持了一场关于预防性医疗保健的圆桌讨论，参加者包括斯坦福医院院长在内的六位行业高管。

在圆桌讨论中，拜登称他刚刚看到的是“未来的实验室”。他还赞扬Holmes主动与FDA合作。“我知道FDA最近完成了对你们这项创新设备的积极评估，”他说，“你们自愿将所有检测项目提交给FDA审查，这体现了你们对自己所做事情的信心。”

公司对员工的控制

一些前员工收到了 Theranos 律师发来的停止侵权函（cease-and-desist letters），因为他们在离职后发布了被认为过于详细的工作描述。sunny 还定期监控员工的电子邮件和浏览历史。他还禁止使用谷歌浏览器，理由是谷歌可能会利用该浏览器监视 Theranos 的研发工作，这显然是胡说八道。

在纽瓦克办公园区工作的员工被禁止使用健身房，因为这可能会导致他们与在该园区租用办公空间的其他公司的员工接触。

在被称为“诺曼底”（Normandy）的临床实验室区域，Edison 设备周围竖起了隔板，以防西门子技术人员在来维修德国制造的机器时看到它们。这些隔板把房间变成了一个迷宫，并封锁了出口。实验室的窗户被贴膜，从外面几乎看不到里面，但公司仍然在内部贴上不透明塑料板。通往实验室房间的走廊门，以及实验室本身，都配备了指纹扫描仪。如果一次有超过一个人进入，传感器就会触发警报，并启动摄像头拍照发送到安保台。至于监控摄像头，它们无处不在。

它们装在深蓝色的半球形罩子里，让人难以判断镜头朝向何处。所有这些表面上是为了保护商业机密，但现在很明显，这也是 Holmes 掩盖她关于Theranos技术现状谎言的一种方式。

Holmes 的名言

她在别人发出质疑时，不正面回答，而是说：This is what happens when you work to change things, first they think you’re crazy, then they fight you, and then all of a sudden you change the world

行为树的缺点

1. 一个简单的操作都需要定义叶子节点，继承类并实现派生方法Init, OnTick， provide port，在工厂类中注册，导致在工程初期的代码量快速增大
2. 当行为树规模变大，XML文件逻辑分散，很难追踪执行路径，复用性并没有想象中高，
3. 最大缺陷：黑板变量，有的人在XML文件里赋值，有的人在C++里赋值，我如果用groot2看行为树，无法看到C++里赋值的情况
4. 黑板机制的副作用：太灵活，没有强类型约束，没有作用域控制
5. switch默认最多6个case，不能直接修改xml文件里的Switch，C++不识别。要想实现更多case，只能自己实现新的 Control 节点，或者说行为树不倾向这种用法
6. C++的逻辑风格是大多数人熟悉的，比如if else, while, 设计模式等等，一个人看另一个人写的代码并不难上手。但是行为树的逻辑类型很多，有的人还会自己定义控制节点和修饰节点。同样的功能，不同人实现的逻辑会很不同，互相难理解，不利于团队协作，其他人难接手以前代码。也就是说行为树编程太灵活，缺乏规范

行为树的优点

1. 有些逻辑，如果在C++里实现或者说用状态机，会非常难理解，代码量膨胀，比如修饰节点

2. 也就是相对状态机的优点，比如这样的逻辑

   1 2 3 4

   去目标点 ├── 直走 ├── 绕障 └── 重新规划路径

   如果用状态机的话，需要考虑状态转移、错误处理、retry逻辑，处理起来比较复杂或者说不符合人的思维，如果用行为树，那就是普通的Fallback顺序节点，每个情况作为一个Fallback的分支，很容易理解

3. 某些情况下可以实现节点复用

4. 官方提供了与ROS2的接口，适合机器人的业务开发，而且是两套接口。

补充

1. tick的运行方式，不符合C++程序员的思维。tick一般不会因为频率而造成CPU开销，sequence with memory 等节点可以跳过已运行完的节点。除非 tick 频率设为 100hz 甚至更高，树又非常深，才会成为性能瓶颈。
2. AsyncNode，没帮你解决线程问题，cancel机制不统一，生命周期容易错

状态机的缺点

1. 在项目中可能增加新状态、减少状态或者改变状态之间的迁移关系，如果状态越来越多，一点小修改都会产生很大的工作量，代码中会出现大量的判断跳转，耦合性太强。代码的逻辑会变得臃肿

状态机是由事件驱动的，状态与执行内容是绑定在一起的。当执行内容需要在多个状态中执行时，各个状态下都需要放置执行内容的逻辑。当业务逻辑代码分散在各处时就不太好维护了

行为树适合做任务调度层，控制复杂流程（回充 / 避障 / 任务切换），用它做所有的决策系统，很不合适。应当是行为树和状态机混合使用。

对于割草机的 直走—->绕障 —-> 重新规划路径，用行为树规划，其中的绕障内部用状态机，

1
2
3
4

去目标点
  ├── MoveStraightAction
  ├── AvoidObstacleAction   <--- 内部是FSM
  └── ReplanAction

在AvoidObstacleAction内部是 FSM：

1
2
3
4
5
6
7

INIT
 ↓
AVOID
 ↓
CHECK
 ↓
SUCCESS / FAIL / RECOVER

行为树不适合表达连续性的流程（如避障），因为它缺乏状态锁定机制，会导致执行不稳定和结构复杂化。

在上面这个例子里，如果避障部分也用行为树，会导致：

1. 结构膨胀
2. 在子树之间频繁切换
3. 调试困难
4. 子树不可复用

同样道理，脱困机制也该用状态机，而不是行为树。

总结

选策略用行为树，连续过程（执行细节）用状态机

• 如果一个任务满足有明确步骤（1. 2. 3.）、中途不能被打断、需要记住进度，使用 FSM

• 如果是存在多种行为选择、需要 fallback 或 retry、可以随时切换状态，使用 BT

1
2
3
4
5

BehaviorTree（高层调度）
		↓
FSM / Planner（决策）
		↓
Controller（控制）

频率控制

1
2
3
4
5

BT tick（10Hz）
      ↓
FSM update（10~20Hz）
      ↓
Controller（50~100Hz）

使用Groot打开行为树文件，有时会报警一大堆：不识别某Action，这是因为xml文件必须具备 TreeNodesModel才能让Groot识别。显然xml的作者不太会用行为树。

此外它还需要：节点类型，端口的名称和类型（输入/输出）。我们不需要手动去添加，工作了太大了。行为树提供了函数来生成:

1
2
3
4
5

BT::BehaviorTreeFactory factory;  
// register here your user-defined Nodes 

std::string xml_models = BT::writeTreeNodesModelXML(factory); 
cout << xml_models <<endl;

可以将 XML 保存到文件中，然后点击 Groot2 中的导入模型按钮。或者手动将输出的 xml_models直接添加到 .xml文件中。

也就是需要先定义Node，然后注册。才能调用writeTreeNodesModelXML，否则不识别Action的名称。当然也必须在 createTreeFromFile之后。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include <iostream>
#include "behaviortree_cpp_v3/action_node.h"
#include "behaviortree_cpp_v3/xml_parsing.h"
#include "behaviortree_cpp_v3/bt_factory.h"
#include "behaviortree_cpp_v3/behavior_tree.h"

using namespace std;
using namespace BT;

class MyClass : public BT::SyncActionNode
{
public:
    MyClass(const std::string& name, [[maybe_unused]] const BT::NodeConfiguration& config):
        BT::SyncActionNode(name, {})
    {
    }
    ~MyClass()
    {
    }
    static BT::PortsList providedPorts()
    {
        return {BT::InputPort<string>("input_code","NULL_ERROR","error code "),
                    BT::InputPort<string>("input_action","NULL_ACTION","input action ")};
    }
    BT::NodeStatus tick()
    {
        return BT::NodeStatus::SUCCESS;
    }
};

int main([[maybe_unused]] int argc, [[maybe_unused]] char ** argv)
{
    BT::BehaviorTreeFactory factory;
    factory.registerNodeType<MyClass>("ClassName");

    auto tree = factory.createTreeFromFile("/home/user/bt.xml");

    std::string xmlmodels = BT::writeTreeNodesModelXML(factory);
    cout << endl << xmlmodels << endl;

    return 0;
}

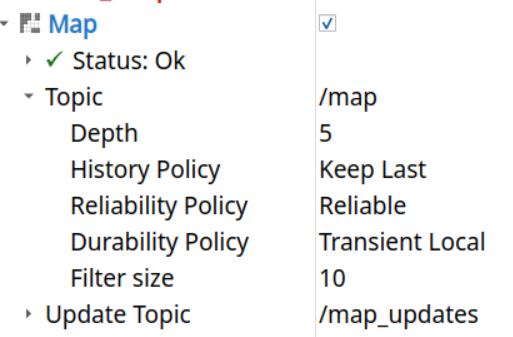
代价地图是在 planner_server 和 controller_server中初始化的。

清除代价地图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

<Action ID="ClearEntireCostmap">
	<input_port name="service_name">Service name</input_port>
	<input_port name="server_timeout">Server timeout</input_port>
</Action>

<Action ID="ClearCostmapExceptRegion">
	<input_port name="service_name">Service name</input_port>
	<input_port name="server_timeout">Server timeout</input_port>
	<input_port name="reset_distance">Distance from the robot above which obstacles are cleared</input_port>
</Action>

<Action ID="ClearCostmapAroundRobot">
	<input_port name="service_name">Service name</input_port>
	<input_port name="server_timeout">Server timeout</input_port>
	<input_port name="reset_distance">Distance from the robot under which obstacles are cleared</input_port>
</Action>

行为树节点部分在clear_costmap_service.cpp，三个类都继承了BtServiceNode

服务端在 clear_costmap_service.cpp， 这里创建了service，编译为 libnav2_costmap_2d_core.so. 构造函数部分可以看到三个service的创建及其名称

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

ClearCostmapService::ClearCostmapService(
  const nav2_util::LifecycleNode::WeakPtr & parent,
  Costmap2DROS & costmap)
: costmap_(costmap)
{
  auto node = parent.lock();
  logger_ = node->get_logger();
  reset_value_ = costmap_.getCostmap()->getDefaultValue();

  clear_except_service_ = node->create_service<ClearExceptRegion>(
    "clear_except_" + costmap_.getName(),
    std::bind(
      &ClearCostmapService::clearExceptRegionCallback, this,
      std::placeholders::_1, std::placeholders::_2, std::placeholders::_3));

  clear_around_service_ = node->create_service<ClearAroundRobot>(
    "clear_around_" + costmap.getName(),
    std::bind(
      &ClearCostmapService::clearAroundRobotCallback, this,
      std::placeholders::_1, std::placeholders::_2, std::placeholders::_3));

  clear_entire_service_ = node->create_service<ClearEntirely>(
    "clear_entirely_" + costmap_.getName(),
    std::bind(
      &ClearCostmapService::clearEntireCallback, this,
      std::placeholders::_1, std::placeholders::_2, std::placeholders::_3));
}

对应3个service

1
2
3

/local_costmap/clear_around_local_costmap
/local_costmap/clear_entirely_local_costmap
/local_costmap/clear_except_local_costmap

问题

编译nav2_costmap_2d后，直接运行ros2 run nav2_costmap_2d nav2_costmap，结果报错

1

[pluginlib.ClassLoader]: Skipped loading plugin with error: XML Document '/home/user/project/install/nav2_costmap_2d/share/nav2_costmap_2d/costmap_plugins.xml' has no Root Element. This likely means the XML is malformed or missing..

如果行为树有节点是Nav2的客户端，在服务端没启动时，服务不可用，行为树运行时会直接报错，不会运行任何节点。

如果没启动服务端，客户端发起请求时会报错

1
2
3

[ERROR] [1754535646.216247848] [nav2_node]: "global_costmap/clear_entirely_global_costmap" service server not available after waiting for 1.00s
[nav2_node-1] terminate called after throwing an instance of 'std::length_error'
[nav2_node-1]   what():  basic_string::_M_create

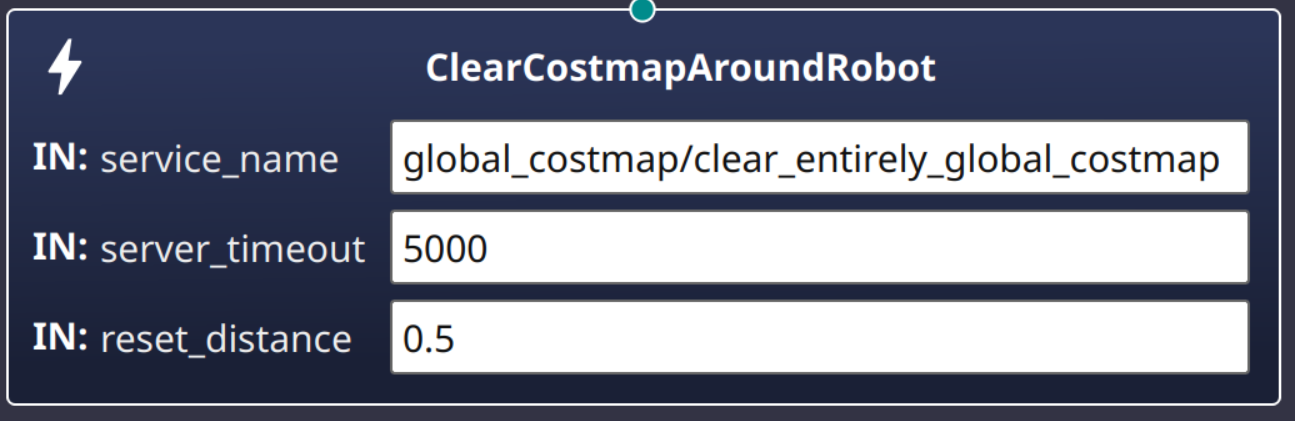
Action和service_name不符合，加载行为树会报错

1

what():  could not create client: create_client() called for existing request topic name rq/global_costmap/clear_entirely_global_costmapRequest with incompatible type navit_msgs::srv::dds_::ClearEntireCostmap_Request_, at ./src/rmw_client.cpp:165, at ./src/rcl/client.c:146

又是和ROS1的有所不同

先执行：ros2 run nav2_map_server map_server --ros-args --param yaml_filename:=map/fishbot_map.yaml

再打开rviz2，把设置都改好

再手动激活和配置节点

1
2

ros2 lifecycle set /map_server configure  
ros2 lifecycle set /map_server activate

跟ROS1有所不同，不会一直发布/map话题。而且/map不会显示所有地图数据，会用- '...'表示，估计是开发者觉得显示一大堆地图数据没有意义。

也可以在运行时使用load_map服务更改地图

Map Server是一个可组合的 ROS2 节点。默认情况下，有一个map_server可执行文件来实例化这些节点之一，但如果需要，也可以将多个地图服务器节点组合到一个进程中。

Nav2 使用 ROS2 参数机制来获取要使用的 YAML 文件名。这实际上引入了一个间接层来获取地图 yaml 文件名。例如，对于一个名为“map_server”的节点，参数文件看起来是这样的：

1
2
3

map_server:
    ros__parameters:
        yaml_filename: "map.yaml"

也可以在一个进程中运行多个地图服务器节点，此时参数文件会按节点名称分隔参数，例如：

1
2
3
4
5
6
7
8

# combined_params.yaml
map_server1:
    ros__parameters:
        yaml_filename: "some_map.yaml"

map_server2:
    ros__parameters:
        yaml_filename: "another_map.yaml"

然后，使用包含两个节点参数的参数文件来启动该进程：process_with_multiple_map_servers __params:=combined_params.yaml

保存地图

ros2 run nav2_map_server map_saver_cli [arguments] [--ros-args ROS remapping args]

比如：ros2 run nav2_map_server map_saver_cli -f test

两个 service

1

ros2 service call /map_server/load_map nav2_msgs/srv/LoadMap "{map_url: /ros/maps/map.yaml}"

1

ros2 service call /map_saver/save_map nav2_msgs/srv/SaveMap "{map_topic: map, map_url: my_map, image_format: pgm, map_mode: trinary, free_thresh: 0.25, occupied_thresh: 0.65}"